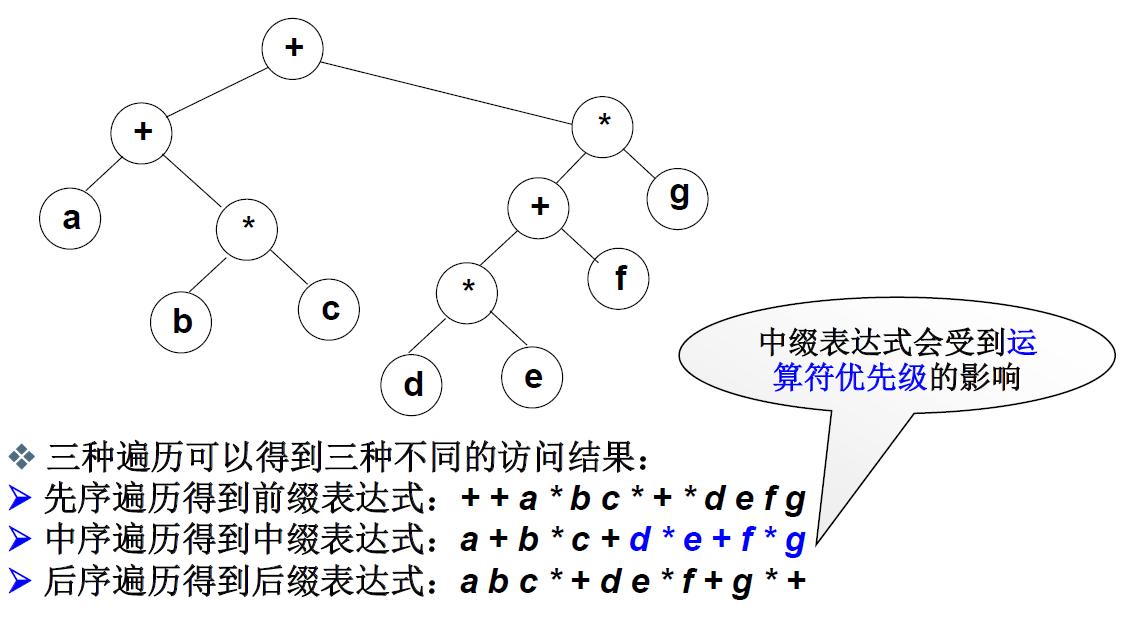
数据结构：二叉树遍历及其堆栈实现和应用

二叉树的非递归遍历

• 使用堆栈

中序

• 遇到一个结点，就把它压栈，并去遍历它的左子树；
• 当左子树遍历结束后，从栈顶弹出这个结点并访问它；
• 然后按其右指针再去中序遍历该结点的右子树。

void InOrderTraversal( BinTree BT )
{ BinTree T=BT;
Stack S = CreatStack( MaxSize ); /*创建并初始化堆栈S*/
while( T || !IsEmpty(S) ){
while(T){ /*一直向左并将沿途结点压入堆栈*/
Push(S,T);
T = T->Left;
}
if(!IsEmpty(S)){
T = Pop(S); /*结点弹出堆栈*/
printf(“%5d”, T->Data); /*（访问）打印结点*/
T = T->Right; /*转向右子树*/
}
}
}

先序

void InOrderTraversal( BinTree BT )
{ BinTree T BT;
Stack S = CreatStack( MaxSize ); /*创建并初始化堆栈S*/
while( T || !IsEmpty(S) ){
while(T){ /*一直向左并将沿途结点压入堆栈*/
Push(S,T);
T = T->Left;
}
if(!IsEmpty(S)){
T = Pop(S); /*结点弹出堆栈*/
printf(“%5d”, T->Data); /*（访问）打印结点*/
T = T->Right; /*转向右子树*/
}
}
}

层序遍历

• 核心问题： 二维结构的线性化，二维到一维

• 问题：会丢失父结点

• 需要一个存储结构保存暂时不访问的结点，比如堆栈、队列。

• 队列实现：遍历从根结点开始，首先将根结点入队，然后开始执行循环：结点出队、访问该结点、其左右儿子入队
  

层序基本过程

• 从队列中取出一个元素；
• 访问该元素所指结点；
• 若该元素所指结点的左、右孩子结点非空， 则将其左、右孩子的指针顺序入队。

代码实现

void LevelOrderTraversal ( BinTree BT )
{ Queue Q; BinTree T;
if ( !BT ) return; /* 若是空树则直接返回 */
Q = CreatQueue( MaxSize ); /*创建并初始化队列Q*/
AddQ( Q, BT );
while ( !IsEmptyQ( Q ) ) {
T = DeleteQ( Q );
printf(“%d\n”, T->Data); /*访问取出队列的结点*/
if ( T->Left ) AddQ( Q, T->Left );
if ( T->Right ) AddQ( Q, T->Right );
}
}

遍历二叉树的应用

输出二叉树的叶结点

• 在二叉树的遍历算法中增加检测结点的“左右子树是否都为空”。

void PreOrderPrintLeaves( BinTree BT )
{
if( BT ) {
if ( !BT-Left && !BT->Right )
printf(“%d”, BT->Data );
PreOrderPrintLeaves ( BT->Left );
PreOrderPrintLeaves ( BT->Right );
}
}

求二叉树的高度

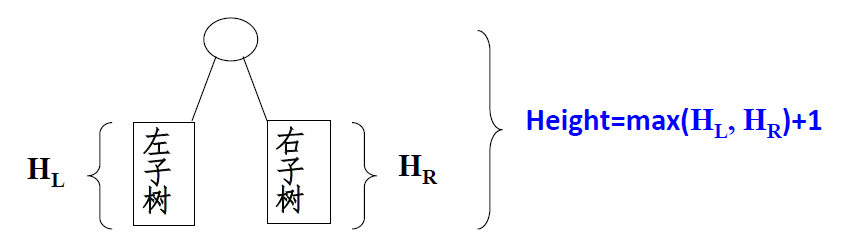
int PostOrderGetHeight( BinTree BT )
{ int HL, HR, MaxH;
if( BT ) {
HL = PostOrderGetHeight(BT->Left); /*求左子树的深度*/
HR = PostOrderGetHeight(BT->Right); /*求右子树的深度*/
MaxH = （HL > HR）? HL : HR; /*取左右子树较大的深度*/
return ( MaxH + 1 ); /*返回树的深度*/
}
else return 0; /* 空树深度为0 */
}

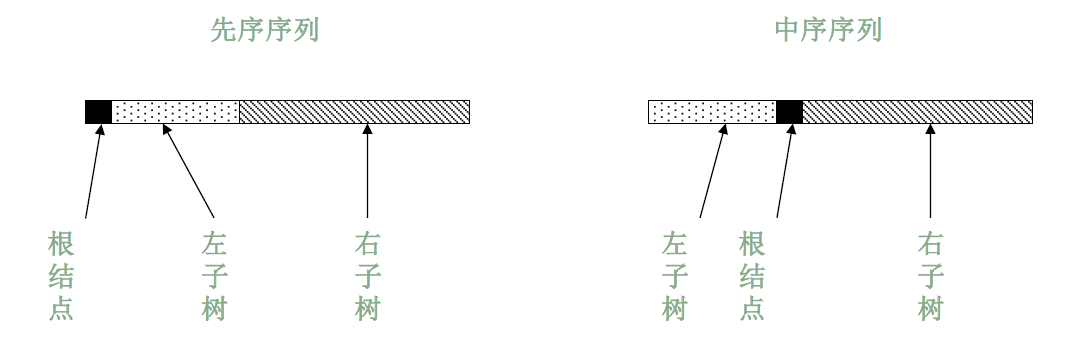
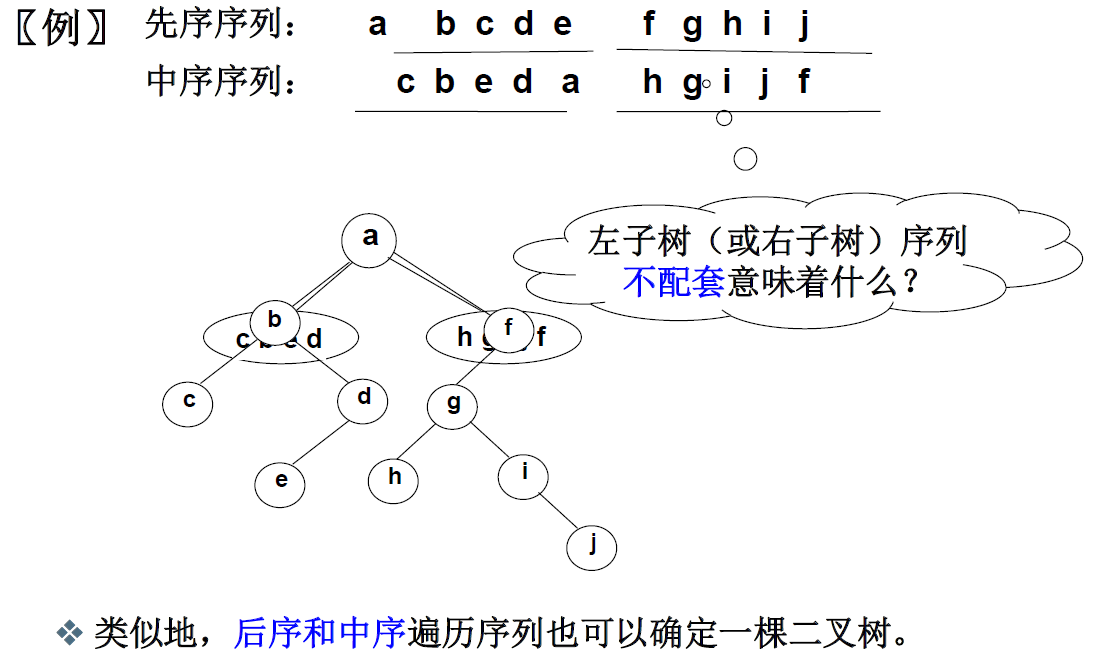
先序和中序遍历序列来确定一棵二叉树

• 根据先序遍历序列第一个结点确定根结点；
• 根据根结点在中序遍历序列中分割出左右两个子序列
• 对左子树和右子树分别递归使用相同的方法继续分解。