最大子列和的几种算法比较
前言
- 最大子列和是一个经典算法问题,在《算法导论》中有一歌股票问题的应用。已知一周的股票价格,考虑在正常的时间顺序下,想在最低价买进,最高价卖出,求出这段区间。
- 可以构建一个新的数组,每一个数都是该天与前一天之差,然后就转化为求最大子列和的问题。
O(n^3)——最差暴力求解
- 算出每一个子列和,大于现有最大值,就更新这个值。
- 比暴力求解算法还多余了一层循环。

O(n^2)——暴力求解
- 算法同最差暴力求解,但稍有优化,却不足够。

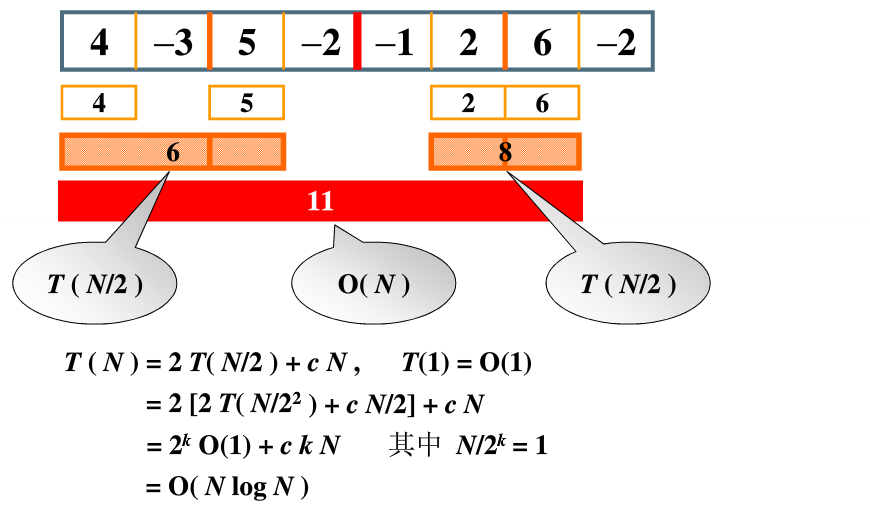
O(nlgn)——分治法
- 把求最大子列分为三种情况:1. 不包含中点值的左端最大子列和。 2. 不包含中点值的右端最大子列和。
- 必包含中点值的最大子列和。
O(n)——在线处理
- 从第一个数开始累加,一旦子列和为负就舍弃前面的子列和,从下一个数并且从0开始重新累加,一旦超过现有的最大值就更新最大值。
- 重点:为负的子列和,不可能使后面的子列和更大!

总结
- 暴力求解的方法是最直观的最容易想到的算法,但是时间复杂度过高。
- 分治法把时间复杂度降低了很多,但是由于使用了递归,空间复杂度大大增加,所以也不实用。
- 在线处理方法空间复杂度和时间复杂度都最优,抓住了问题的本质,同时提供了一个在线处理的思想,不断丢弃无用的东西,从而简化算法。