概率论04 随机变量

作者：Vamei 出处：http://www.cnblogs.com/vamei 欢迎转载，也请保留这段声明。谢谢！

 

我们了解了“样本空间”，“事件”，“概率”。样本空间中包含了一次实验所有可能的结果，事件是样本空间的一个子集，每个事件可以有一个发生的概率。概率是集合的一个“测度”。

这一讲，我们将讨论随机变量。随机变量(random variable)的本质是一个函数，是从样本空间的子集到实数的映射，将事件转换成一个数值。根据样本空间中的元素不同(即不同的实验结果)，随机变量的值也将随机产生。可以说，随机变量是“数值化”的实验结果。在现实生活中，实验结果可以是很“叙述性”，比如“男孩”，“女孩”。在数学家眼里，这些文字化的叙述太过繁琐，我们为什么不能拿数字来代表它们呢？

(数学家恐怕是很难成为文学家吧？)

 

离散随机变量

在连续掷两次硬币的例子中，样本空间为:

$$\Omega = \{ HH, HT, TH, TT \}$$

这样的实验结果可以有很多数值化的方法，比如定义HH为400， HT为30， TH为0.2，TT为1。要注意的是，这里是用某个数字来代表样本空间的某个元素，这个数字并不是概率值。

如何对样本空间的元素数值化是根据现实需求的。比如说，根据出现正面的次数，我们将赢取不同的奖励。那么在分析时，可以取“结果中正面的次数”为随机变量。这样一个随机变量将有2, 1, 0三种可能的取值。该随机变量只能取离散的几个孤立值，这样一种随机变量称为离散随机变量。

映射关系如下:

实验结果	随机变量
HH	2
HT	1
TH	1
TT	0

 

我们通常用一个大写字母来表示一个随机变量，比如X。

如果样本空间中的每个结果等概率，那么随机变量取值可能性为:

$$P(X=2) = 0.25$$

$$P(X=1) = 0.5$$

$$P(X=0) = 0.25$$

当X取0,1,2之外的值时，概率为0。注意到，X=1这个事件，实际上包含了两个元素，HT, TH。因此，X=1出现的概率较高。所有可能取值的概率和为1。

[$P(X=x)$]表示了随机变量在不同取值下的概率，称为概率质量函数(PMF, probability mass function)。我们将看到其他的表示概率分布的方式。

 

累积分布函数

上面的函数列出了每个取值的对应概率。等价的，我们可以用累积分布函数(CDF, cumulative distribution function)来表示随机变量的概率分布状况。在累积分布函数，我们列出的，总是随机变量X，在小于x的这个区间的概率和。当x增大时，X < x包含的结果增加，概率和也相应增加。当x为正无穷时，实际上是所有情况的概率和，那么累积分布函数为1。

严格的定义为:

$$F(x) = P(X \le x), -\infty < x < \infty$$

 

我们可以绘制上面例子的CDF。

 

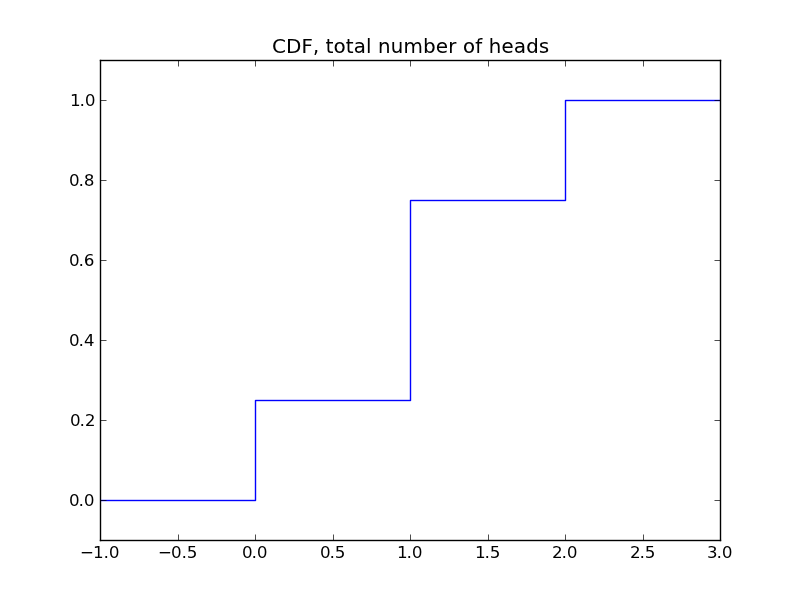
这样的累积分布函数似乎并不比概率质量函数来得方便。但在后面，我们会很快看到它的优势。即它可以同时用于离散随机变量和连续随机变量。

 

上面的图片可以用如下代码生成:

# By Vamei
# Plot the CDF of total number of heads in two flips

import matplotlib.pyplot as plt
x = [-1, 0, 0, 1, 1, 2, 2, 3]
y = [0, 0, 0.25, 0.25, 0.75, 0.75, 1.0, 1.0]

fig = plt.figure()
ax  = plt.subplot(111)

ax.plot(x, y)
ax.set_ylim([-0.1, 1.1])
ax.set_title("CDF, total number of heads")
plt.show()

 

连续随机变量

随机变量还可以是连续取值，这样的随机变量称为连续随机变量(continuous random variable)。比如，一个随机变量，可以随机的取0到1的任意数值。

当这样取值时，任意区间能实际上都有无穷多个结果。比如，我们测量温度，可以有1度和2度，但两者之间，还可以有1.1度，1.003度，1.658度等等无穷种结果。这样的话，每个结果的可能性都是无穷小。我们讨论的是某个区间内的概率，即[$P(a<X<b)$]，而不是具体某一数值的概率。在这样的情况下，分到各个结果的概率都无限趋近于0。显然，我们无法用概率质量函数来描述连续随机变量的分布。

 

我们这里遇到的困境是现代数学的一个相当的困扰。考虑一个线段，它是点的集合，并且有“长度”这样的测度。然而，线段上有无穷个多个点。讨论“每个点的长度”是完全没有意义的。将线段换成区间，将点换成取值，将长度换成概率，我们发现这两个问题异常相似。另一方面，我们知道，可以从线段上截取某一小段，而这一小段是可以有“长度”的。连续随机变量的概率定义，正依赖于此：对于连续随机变量，我们只讨论某个区间，比如从1.2到1.4这一区间的概率，而不讨论具体某个点，比如1.3的概率。 

 

观察一个很简单的连续随机分布。假设我们有一个随机数生成器，产生一个从0到1的实数，每个实数出现的概率相等。这样的一个分布被称为均匀分布(uniform distribution)。直觉告诉我们，相同长度的每一段区间，对应的概率都相同。由此，[0, 0.5]是整个区间的一半，概率为1/2。对于均匀分布来说，概率正好和区间长度这一测度等同。

 

我们尝试用更正式的方式来描述分布。累积分布函数本身就表示随机变量在一个区间概率，所以可以直接用于连续随机变量。即

$$F(x) = P(X \le x), - \infty < x < \infty$$

对于均匀分布来说，它的累积分布函数是:

$$F(x) = 0, x < 0$$

$$F(x) = x, 0 \le x \le 1 $$

$$F(x) = 1, x > 1$$

 

它类似从线段的一头到某一点的“长度”。这样，我们就知道了从起点到每一点的长度。如果我们想知道某个特定区间[a, b]的概率，它就是F(b) - F(a)。

 

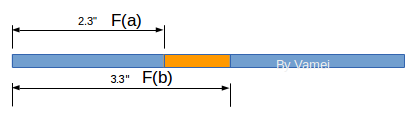
借用“无穷小”的概念，我们可以构建概率密度函数(PDF，probability density function)。粗糙的讲，我们在某个点附近取一个“无穷小”段，该小段的区间长度为dx，而这个“无穷小”段对应的概率为dF，那么该点的概率密度为dF/dx。这实际上是微积分的领域。

概率密度函数可以代替累积分布函数，来表示一个连续随机变量的概率分布:

$$f(x) = \frac{dF(x)}{dx}$$

即密度函数是累积分布函数的微分，或者说，

$$F(x) = \int_{-\infty}^x f(u)du$$

即累积分布函数是密度函数从负无穷到x的积分。

 

密度函数满足:

$$\int_{-\infty}^{+\infty} f(u)du = 1$$

 

均匀分布的密度函数可以写成:

$$f(x) = \left\{ \begin{array}{l} 1, 0 \leq x \leq 1 \\ 0, x<0 \, or \, x>1 \end{array}\right.$$

 

可以画出该密度函数

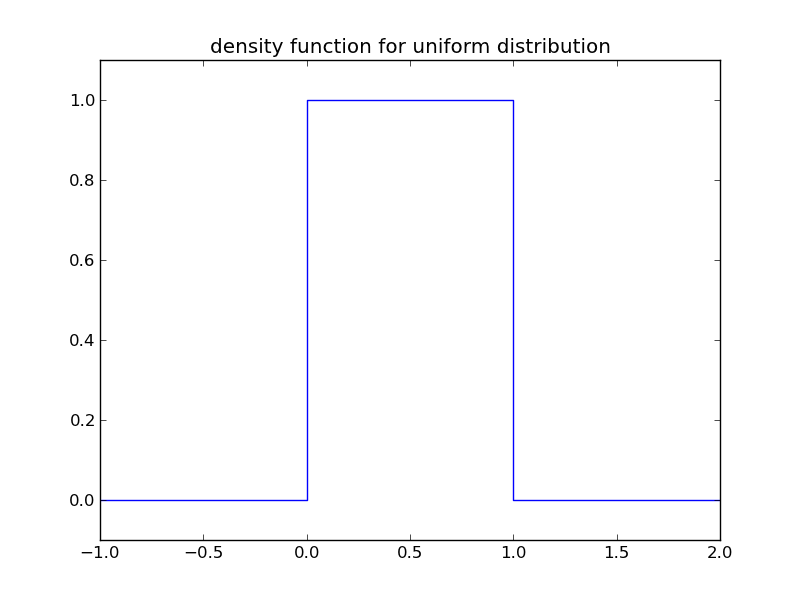
对一个函数的积分，获得的是该函数曲线下的面积。因此，密度曲线下某个区间的面积，就是密度概率函数的积分，代表了随机变量在该区间的概率。概率密度函数就可以非常直观的通过“面积”，来表示概率的大小。

从负无穷到正无穷积分，就代表了所有可能结果的概率和，即为1。

 

上面的图片可以利用下面代码生成:

# By Vamei
# Density function for uniform distribution

import matplotlib.pyplot as plt
x = [-1, 0, 0, 1, 1, 2]
y = [0, 0, 1, 1, 0, 0]

fig = plt.figure()
ax = plt.subplot(111)

ax.plot(x, y)
ax.set_xlim([-1, 2])
ax.set_ylim([-0.1, 1.1])
ax.set_title("density function for uniform distribution")
plt.show()

 

总结

随机变量，随机变量的概率分布

累积分布函数

密度函数

 

欢迎继续阅读“数据科学”系列文章