【动态主席树详解】ZOJ-2112 Dynamic Rankings
去年的9月份的时候学习了主席树,当时用了一天的时间理解代码,之前没有学过动态开点的线段树,所以很懵逼,写了一篇自我感觉易懂的笔记。
相应的做了几道题目之后,开始学习动态主席树,当时可能有些浮躁,看了两天的博客,还是不懂。就搁置了到现在,昨天的时候看了一道题目,可以使用动态主席树也可以使用CDQ分治,看完题目之后带修改的主席树思路直接崩出来了,所以下定决心,把动态主席树搞完,用了一天的时间翻了好多博客,搞懂怎么回事了。写一篇自我感觉良好的博客。
思想
从最原始的方法看起:
比如原序列:1 5 6 2 3 9 8,现在我要把第四位2改为7,理论上说,我们修改一个数字,首先要消除原数字对序列的影响,再添加新的数,然后再产生新的影响;现在2对序列的影响是:第四位以及到最后一位的对应的所有前缀树,每个前缀树中包含2的区间对应的节点与原来比都加上了1,要消除这些影响,我们要对4-n颗前缀树的所有包含2的区间的节点都要减去1,然后再把第四位改为7,再对第4-n颗前缀树的所有包含7的区间的节点都要加上1,到此,更新就结束了。
按照上述方法,复杂度太高,无法接受。
这时可使用树状数组套线段树来维护修改产生的影响。
参考带修改的树状数组:
当修改第 i 个值的时候,会影响树状数组中第 i 个及其以后的节点的值。这时我们的做法是让x 和 x+lowbit(x) ...加上前后的差值。
求区间[l , r] 的和时,答案为\(pre[r]-pre[l-1]+query(r)-query(l-1)\)。\(pre[i]\)表示前 i 个数的前缀和。\(query[i]\)表示前 i 个数字修改时产生的差值前缀和。
如题,已知一个数列,你需要进行下面两种操作:
- 将某一个数加上 xx
- 求出某区间每一个数的和
树状数组代码:
#include <bits/stdc++.h>
#define emplace_back push_back
#define pb push_back
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;
const int N = 2e6 + 10;
ll lowbit(ll x){
return x&(-x);
}
ll arr[N],pre[N],tree[N],n,m;
void update(ll pos,ll val){
while(pos<=n){
tree[pos]+=val;
pos+=lowbit(pos);
}
}
ll query(ll l){
ll sum=0;
while(l>0){
sum+=tree[l];
l-=lowbit(l);
}
return sum;
}
int main(){
scanf("%lld%lld",&n,&m);
for(ll i=1;i<=n;i++){
scanf("%lld",&arr[i]);
pre[i]=pre[i-1]+arr[i];
}
for(ll i=1;i<=m;i++){
ll op,l,r;
scanf("%lld%lld%lld",&op,&l,&r);
if(op==1){
update(l,r);
}
else{
printf("%lld\n",pre[r]-pre[l-1]+query(r)-query(l-1));
}
}
return 0;
}
同上对于动态主席树的修改,也用一个树状数组来维护改变,假如我们现在修改第 i 颗主席树,那么我们需要在第 i 颗主席树上找到相应的区间的节点,进行修改。所以我们维护改变的树状数组的节点应该是一颗线段树。才能维护发生的变化。
这时\(pre[r]-pre[l-1]\)就相当于在初始建立的主席树上查询,\(query[r]-query[l-1]\)就相当于在树状数组上查询发生的改变。
(多考虑一下)
大致流程
题解大致流程如下:
下面来演示一下建树到查询的过程:
比如此题的第一个案例
5 3 3 2 1 4 7 Q 1 4 3 C 2 6 Q 2 5 3先将序列以及要更新的数(C操作)离散化
即3 2 1 4 7 、 6 ---->(排序) ----> 1 2 3 4 6 7
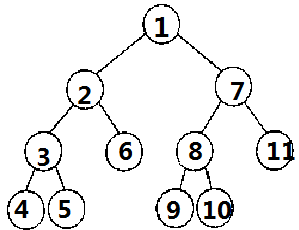
那么我们就需要建一棵这样的树:
(圈里的都是结点的编号, 4、5、6、9、10、11号结点代表的分别是1、2、3、4、6、7)
(4、5、9、10你也可以任意作为6或11的儿子, 递归生成的是类似这样的, 这并不重要)
对于3 2 1 4 7(先不管需要更新的6)建完树见下图(建树过程同静态的,不明白的戳这里,上篇博客有讲)
(红色的是个数, 相同结点的个数省略了,同前一棵树)
对于C操作之前的Q,就跟静态的类似,减一减 找就好了
然后下面要更新了
对于更新, 我们不改变这些已经建好的树, 而是另建一批树S,用来记录更新,而这批线段树,我们用树状数组来维护
也就是树状数组的每个节点都是一颗线段树
一开始,S[0]、S[1]、S[2]、S[3]、S[4]、S5这些都与T[0]相同(也就是每个节点建了一棵空树,即刚开始没有产生影响)
对于C 2 6 这个操作, 我们只需要减去一个2,加上一个6即可
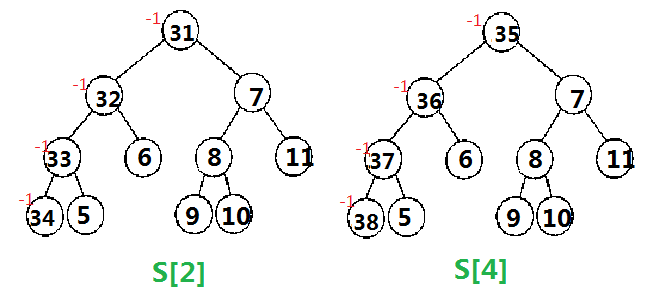
对于消除2的影响
2在树状数组中出现的位置是 2,从位置2开始进行树状数组的更新,改变了2和2+lowbit(2)=4 这两个位置,
因此要更新的是S[2]和S[4]这两个节点中的树
删去2后是这样
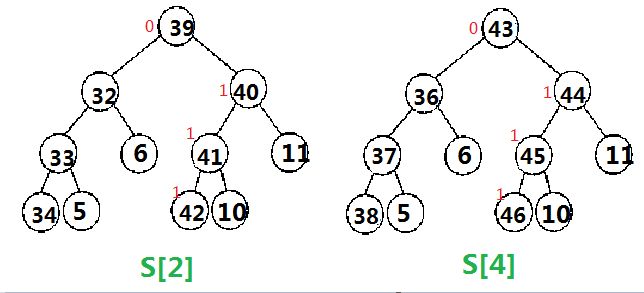
加上一个6 (同样是对于2号位置, 因此需要更新的仍是S[2]和S[4])
加上之后是这样
代码
代码中有注释:
#include <bits/stdc++.h>
#define emplace_back push_back
#define pb push_back
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;
const int N = 2e6 + 10;
vector<int>v;//离散化使用的vector
int getid(int x){//获取 x 离散化后的值
return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
int T[N],S[N],arr[N],use[N],tot,n,m;
// T[i]表示初始建立的第 i 颗主席树的根节点
struct note{//主席树节点
int l,r,size;
}node[N*40];
struct Q{//操作
int l,r,k,op;
}q[N];
int lowbit(int x){
return x&(-x);
}
void build(int &rt,int l,int r){//建立空树
node[rt=++tot].size=0;
if(l==r) return ;
int mid=(l+r)>>1;
build(node[rt].l,l,mid);
build(node[rt].r,mid+1,r);
}
void update(int &rt,int lst,int l,int r,int pos,int val){//更新
node[rt=++tot]=node[lst];node[rt].size+=val;
if(l==r) return;
int mid=(l+r)>>1;
if(pos<=mid) update(node[rt].l,node[lst].l,l,mid,pos,val);
else update(node[rt].r,node[lst].r,mid+1,r,pos,val);
}
void modify(int x,int pos,int val){//这一步其实就是树状数组中的单点修改,只不过把权值的加减换成了在线段树上的更新
while(x<=n){
update(S[x],S[x],1,v.size(),pos,val);
x+=lowbit(x);
}
}
int Sum(int x){//这一步是树状数组中的查询,rel 表示的是差值的前缀和
int rel=0;
while(x>0){
rel+=node[node[use[x]].l].size;
x-=lowbit(x);
}
return rel;
}
int query(int x,int y,int lst,int rt,int l,int r,int k){//整个查询
//l,r 表示当前节点维护的区间,k 为查询第 k 大。
if(l>=r) return l;
int mid=(l+r)>>1;
int sum=Sum(y)-Sum(x)+node[node[rt].l].size-node[node[lst].l].size;
// Sum(y) - Sum(x) 是修改在区间[x+1,y]产生的影响,后面就是静态主席树的查询
if(sum>=k){//向左子树递归查询
for(int i=y;i;i-=lowbit(i)){
use[i]=node[use[i]].l;
}
//此时对应修改的查询也要向左子树表示的值域走,节点变成该节点的左子树
for(int i=x;i;i-=lowbit(i)){
use[i]=node[use[i]].l;
}
return query(x,y,node[lst].l,node[rt].l,l,mid,k);
}
else{//右子树递归查询
//同上
for(int i=y;i;i-=lowbit(i)){
use[i]=node[use[i]].r;
}
for(int i=x;i;i-=lowbit(i)){
use[i]=node[use[i]].r;
}
return query(x,y,node[lst].r,node[rt].r,mid+1,r,k-sum);
}
}
int main(){
int _;
scanf("%d",&_);
while(_--){
v.clear();
tot=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&arr[i]);
v.pb(arr[i]);
}
for(int i=1; i<=m; i++){
char tmp[2];
scanf("%s",tmp);
if(tmp[0]=='Q'){
scanf("%d%d%d",&q[i].l,&q[i].r,&q[i].k);
q[i].op=0;
}
else{
scanf("%d%d",&q[i].l,&q[i].r);
q[i].op=1;
v.pb(q[i].r);//把改变后的数字也要添加进去,进行离散化
}
}
// printf("fuck\n");
sort(v.begin(),v.end()),v.erase(unique(v.begin(),v.end()),v.end());
build(T[0],1,v.size());//建立空树
for(int i=1;i<=n;i++) update(T[i],T[i-1],1,v.size(),getid(arr[i]),1);//和静态主席树一样,将点更新进去
for(int i=1;i<=n;i++) S[i]=T[0];//把树状数组的所有节点都搞成空树,表示初始时并没有产生影响
for(int i=1;i<=m;i++){
if(q[i].op==0){
//此时use数组存放的是,在查询的过程中用到的树状数组的节点号
//在查询的时候use 数组会发生变化,那时存放的是查询过程中使用到的树状数组维护的线段树中的节点号
for(int j=q[i].l-1;j;j-=lowbit(j)){
use[j]=S[j];
}
for(int j=q[i].r;j;j-=lowbit(j)){
use[j]=S[j];
}
printf("%d\n",v[query(q[i].l-1,q[i].r,T[q[i].l-1],T[q[i].r],1,v.size(),q[i].k)-1]);
}
else{
modify(q[i].l,getid(arr[q[i].l]),-1);//消除修改前的数字的影响
modify(q[i].l,getid(q[i].r),1);//新增修改后的数字的影响
arr[q[i].l]=q[i].r;
}
}
}
// getchar();
// getchar();
return 0;
}
/*
*/
参考博客:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号