HDU-4725 The Shortest Path in Nya Graph 最短路

The Shortest Path in Nya Graph

题意

现在有n个点，m条有权边，无向图，给出每个点所属的层，相邻的层之间有一条权值为c的边，求1-n的最短路。

思路

这题建图方式有些特殊。

刚开始想的是n+1~2*n代表1-n层，每层和每层的点建立权值为0的双向边，相邻的层建立权值为c的双向边，但是这样会有问题。

比如

3 0 3

1 2 1

1 3 3

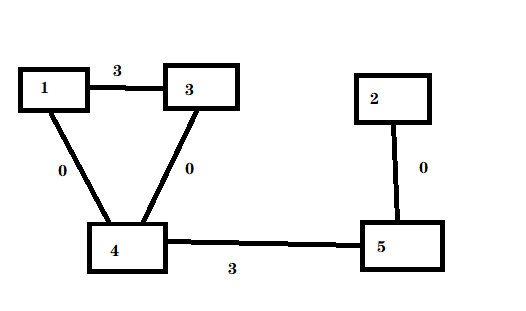
图中均是无向边。

这样建图的话1-3的最短路直接变成0了，也就是同一层的最短路都会变成0.

正确的建图：

每层向每层的点建立权值为0的单向边。

然后每个点向相邻层建立权值为c的单向边。

代码

#include<stdio.h>
#include<algorithm>
#include<queue>
#include<string.h>
#include<string>
#include<math.h>
#define pb push_back
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=1e5+10;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;
const double eps=1e-14;

struct Edge
{
    int to,next,w;
} edge[N*10];
int tot,head[N*2];
void add(int u,int v,int w)
{
    edge[tot].to=v;
    edge[tot].w=w;
    edge[tot].next=head[u];
    head[u]=tot++;
}
struct note
{
    int u,val;
    note(int a,int b):u(a),val(b) {}
    bool operator <(const note &a)const
    {
        return val>a.val;
    }
};
int dis[N*2],vis[N*2];
void dijkstra(int aga,int n)
{
    for(int i=1; i<=2*n; i++)
    {
        vis[i]=0;
        dis[i]=inf;
    }
    dis[aga]=0;
    priority_queue<note>q;
    q.push(note(aga,0));
    while(!q.empty())
    {
        note now=q.top();
        q.pop();
        int u=now.u;
        if(vis[u])
            continue;
        vis[u]=1;
        for(int i=head[u]; i!=-1; i=edge[i].next)
        {
            int v=edge[i].to,w=edge[i].w;
            if(vis[v])
                continue;
            if(dis[v]>dis[u]+w)
            {
                dis[v]=dis[u]+w;
                q.push(note(v,dis[v]));
            }
        }
    }
}
int main()
{
    int T,cas=0;
    scanf("%d",&T);
    while(T--)
    {
        tot=0;
        memset(head,-1,sizeof(head));
        int n,m,c;
        scanf("%d%d%d",&n,&m,&c);
        for(int i=1; i<=n; i++)
        {
            int x;
            scanf("%d",&x);
            add(n+x,i,0);//当前层向点建立权值为0的单向边
            /*点向相邻层建立权值为c的单向边*/
            if(x>1) add(i,n+(x-1),c);
            if(x<n) add(i,n+x+1,c);
        }
        for(int i=1; i<=m; i++)
        {
            int u,v,w;
            scanf("%d%d%d",&u,&v,&w);
            add(u,v,w);
            add(v,u,w);
        }
        printf("Case #%d: ",++cas);
        dijkstra(1,n);
        if(dis[n]==inf)
            printf("-1\n");
        else
            printf("%d\n",dis[n]);
    }
    return 0;
}