杂项算法小总结
前言
很多知识不好整理,这篇文章总结一些杂乱的东西,涉及的内容有,\(\texttt{RMQ}\),矩阵乘法(本来应该写在代数里面的,但我的代数知识少得可怜,就写在杂项里面了),高斯消元,\(\texttt{2-SAT}\),扫描线,随机化与模拟退火(还没学,学了会写的)。
RMQ
\(RMQ\),即区间最值询问,是一类查找区间最值的问题,这里讲一下比较有名的在线算法\(ST表\)。
\(ST\)表,本质上是一种\(dp\),设\(f[i][j]\)表示序列中第\(i\)个数开始向后\(2^j\)个数这个区间的最值,那么初始状态\(f[i][0]=a[i]\),\(dp\)方程为:
\(f[i][j]=max/min(f[i][j-1],f[i+(1<<(j-1))][j-1])\)
从中我们可以看出,从\(i\)开始后的\(2^j\)个数,我们把它分成了两段,一段是第\(i\)个数到第\(i+(1<<(j-1))-1\)个数,一段是第\(i+(1<<(j-1))\)个数到第\(i+(1<<j)-1\)个数,也就是这中间的\(2^j\)个数。
以上是预处理部分,现在如果我们要考虑查询\([l,r]\)这个区间呢?看图(来自某\(C\)姓教练)
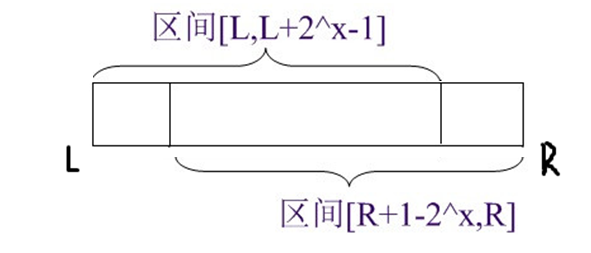
在此,\(x_{max}=log(r-l+1)/log(2)\)。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,a[100005],b[100005],maxn[100005][25],minn[100005][25];
void rmq()
{
for(int j=1;j<20;j++)
for(int i=1;i<=n;i++)
if(i+(1<<j)-1<=n)
maxn[i][j]=max(maxn[i][j-1],maxn[i+(1<<(j-1))][j-1]),minn[i][j]=min(minn[i][j-1],minn[i+(1<<(j-1))][j-1]);
}
int ask(int l,int r)
{
int x=log(r-l+1)/log(2);
int maxx,minx;
maxx=max(maxn[l][x],maxn[r-(1<<x)+1][x]);
minx=min(minn[l][x],minn[r-(1<<x)+1][x]);
return maxx*minx;
}
signed main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
scanf("%lld",&a[i]),maxn[i][0]=minn[i][0]=a[i];
for(int i=1;i<=n;i++)
scanf("%lld",&b[i]);
rmq();
for(int i=1;i<=n;i++)
printf("%lld\n",ask(i-b[i]+1,i));
return 0;
}
矩阵乘法
矩阵乘法是代数的中的知识,两个矩阵相乘的结果自然也是矩阵,那么它的运算法则是什么呢?
设一个\(m*n\)的矩阵为\(A\),一个\(p*m\)的矩阵为\(B\),那么这两个矩阵的乘积矩阵\(C\)的大小就应该是\(m*m\)。
设有矩阵
设有另一个矩阵
那么两者相乘的结果就应该是
也就是说,矩阵之间的乘法是第一个矩阵的行乘第二个矩阵的列。
根据矩阵的运算法则,我们不难看出,矩阵是满足乘法分配律和乘法结合律的,但是矩阵不满足乘法交换律,一旦交换,结果矩阵就会产生变化。
矩阵乘法在\(OI\)中主要运用于优化递推式,有的时候\(O(n)\)的复杂度也许会高达\(1e9\)甚至\(1e12\),这个时候如果有矩阵乘法(严格来说是矩阵快速幂)的优化,复杂度就可以降为\(O(logn)\),可以接受。
只要我们把递推式写了出来,矩阵一般都比较好构造。
矩阵加速
#include<cstdio>
#include<cstring>
using namespace std;
#define ll long long
const ll mod=1e9+7;
struct node
{
ll m[3][3];
// node(){memset(m,0,sizeof m);}
}u,v;
//u.m[3][3]=
//{
// {0,1,0},
// {0,1,0},
// {0,1,0}
//};
//v.m[3][3]=
//{
// {1,0,1},
// {1,0,0},
// {0,1,0}
//};
void init()
{
memset(u.m,0,sizeof(u.m));
memset(v.m,0,sizeof(v.m));
u.m[0][1]=u.m[1][1]=u.m[2][1]=1;
v.m[0][0]=v.m[1][0]=v.m[0][2]=v.m[2][1]=1;
}
node mul(node a,node b)
{
node t;
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
{
t.m[i][j]=0;
for(int k=0;k<3;k++)
t.m[i][j]=(t.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
}
return t;
}
node pow(ll b)
{
while(b)
{
if(b&1) u=mul(u,v);
v=mul(v,v);
b>>=1;
}
return u;
}
ll T;
int main()
{
scanf("%lld",&T);
while(T--)
{
init();
ll p;
scanf("%lld",&p);
if(p<=3)
{
printf("1\n");
continue;
}
node ans=pow(p);
printf("%lld\n",u.m[1][0]);
}
return 0;
}
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
const int mod=1e9+7;
ll n,k;
struct node
{
ll m[105][105];
}a;
node mul(node a,node b)
{
node t;
// memset(t,0,sizeof(t));
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
t.m[i][j]=0;
for(int k=1;k<=n;k++)
t.m[i][j]=(t.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
}
return t;
}
node pow(node a,ll k)
{
node ans=a,b=a;
k--;
// memset(ans,0,sizeof(ans));
while(k)
{
if(k&1) ans=mul(b,ans);
b=mul(b,b);
k>>=1;
}
return ans;
}
int main()
{
scanf("%lld%lld",&n,&k);
for(ll i=1;i<=n;i++)
for(ll j=1;j<=n;j++)
scanf("%lld",&a.m[i][j]);
a=pow(a,k);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
printf("%lld ",a.m[i][j]);
printf("\n");
}
return 0;
}

