分形的豪斯多夫维数（分数维度）

我们在普通的几何学研究中，通常面对的都是整数维的图形，如一维的线、二维的面、三维的体。然而在1918年，德国的数学家豪斯多夫（Hausdorff）提出了“分数维”的概念。半个世纪以后，法国的数学家芒德布罗（D. Mandelbrot）创造出了分形（fractal）一词，词根是拉丁语fractus（破碎）。分形具有分数的维度。

康托尔三分集是最早出现的分形。我们把[0,1]三等分，然后去掉中间的那一部分，得到[0,1/3]和[2/3,1]两部分。我们再把这两部分的分别三等分，然后去掉中间的那一部分，得到[0,1/9]、[2/9,1/3]、[2/3,7/9]和[8/9,1]四部分，如此反复地重复下去，所得到的图形就是康托尔三分集。

 

分形一般都是像上述的康托尔三分集那样通过无穷操作或者迭代得到的，它们都具有“自相似性”，即局部与整体相似。作为一种特殊的几何图形，它们最独特的地方就在于它们的维度——分数维度，下面我们来研究一下它们的维度，即豪斯多夫维数。

我们首先先来观察一下普通几何图形的维数。在二维图形中，如果我们可以通过面积来衡量它们的大小。将一个正方形的边长变为原先的1/n，那么它的面积就变为了原先的\((1/n)^2\)，也就是说我可以通过\(n^2\)个小正方形组合原正方形。

在三维空间中类似于二维空间，我们可以使用\(n^3\)个边长为\(1/n\)的小正方体组成一个边长为1的正方体。

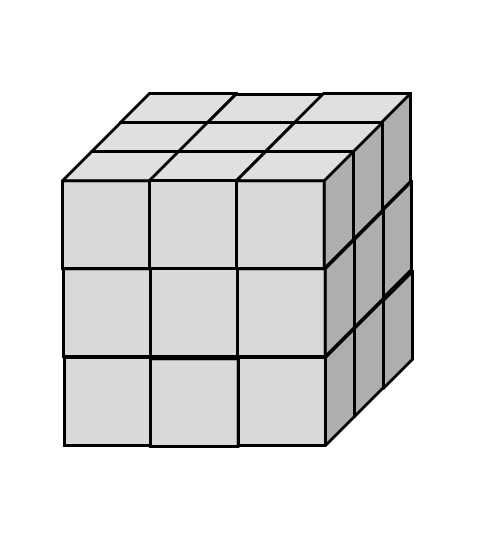
由此，我们可以推断，对于一个维度为k的图形，如果我们可以使用M个相等的部分组成，且这些部分在先行尺度上是原图形的1/n，那么k、n和N应当具有如下的关系式

$M*(1/n)^k=1$

通过化简可得，\(k=\frac{logM}{logn}\)，这就是豪斯多夫维数。

对于刚刚所说的康托尔三分集，他可以由相同的两部分组成，且每一部分在先行尺度上都是原先的1/3，那么它的维数就是log2/log3=0.63

对于另一个著名的分形科赫曲线（科赫雪花），它是在一条线段上作三等分，一中间的部分为底作等边三角形，再将底边去掉，得到相同的四部分，然后再在每一部分上重复上述操作，得到科赫曲线（如果将初始的线段换成等边三角形，对每一条边都进行上述操作，得到的就是科赫雪花）。

 

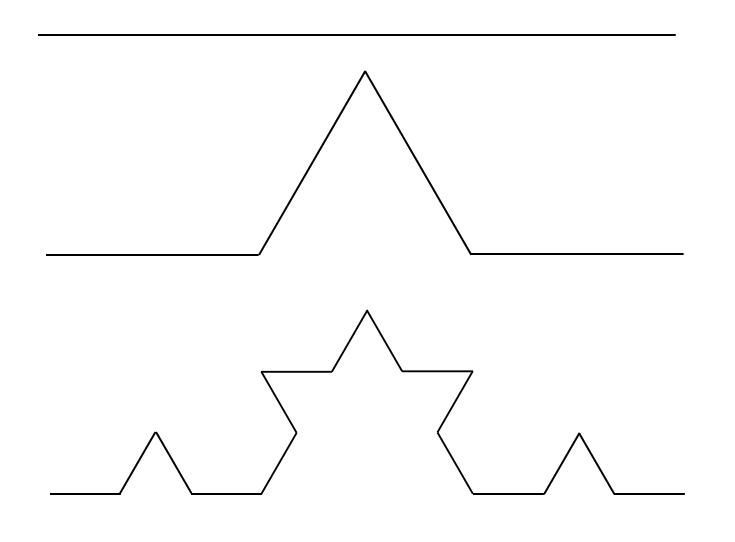
我们可以看到，科赫曲线可以被分成相同的四部分，每一部分在线性尺度上都是原图像的1/3，它的维度就是log4/log3=1.26。它是一个介于一维和二维之间的曲线，它可以通过无穷大的周长围住有限的面积。