在圆周上随机的n个点可以被半圆周覆盖的概率

在圆周上独立地随机选取n个点，那么这n个点可以被半圆周覆盖的概率是多少呢？我们可以先思考这样的一件事，如果我们已经选取了n-1个点，且这n-1个点可以被半圆周覆盖。我们可以将这n-1个点与圆心连线，得到n-1条线段（如图一），我们不妨把这n-1条线段所成夹角的最大值记为\(α_{n-1}\)。延长形成\(α_n-1\)的两边如图一，得到两个大小为\(Π-α_{n-1}\)的夹角。

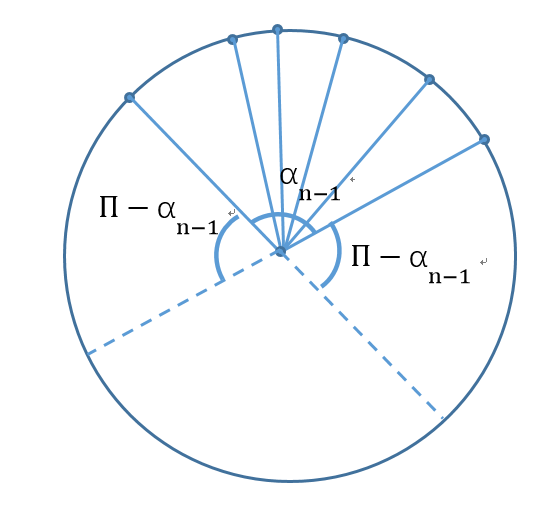
我们很容易可以看出来，如果加入第n个点，使得这n个点能被半圆周覆盖，则第n个点必须要位于上图中虚线上方的圆周上，对于上图来说这个概率就是

$P=\frac{(Π-α_{n-1})+(Π-α_{n-1})+α_{n-1}}{2Π}=\frac{2Π-α_{n-1}}{2Π}$           ①

为了得到前n-1个点满足可以被半圆周覆盖时，加入第n个点依然可以被半圆周覆盖的概率，我们需要找出α的期望。对于α2，也就是圆周上任意两点与圆心连线所得夹角，这个角的大小均匀地分布在0到Π范围内，因此我们可以很容易地得到

$E(α_2)=Π/2$

如果此时，我们加入第三个点，且假设加入第三个点后，这三个点依然可以被半圆周覆盖，类似于积分，如果第三个点位于\(α_2\)内，则\(α_3=α_2\)，如果位于两侧Π-\(α_2\)内，则α3的大小均匀地分布在\(α_2\)到Π之间，我们可以计算出\(α_3\)的期望

$E(α_3)=α_2\frac{α_2}{2Π-α_2}+\frac{Π+α_2}{2}\frac{2(Π-α_2)}{2Π-α_2}=\frac{Π^2}{2Π-α_2}=2/3Π$ 

同理，如果前n-1个点可以被半圆周覆盖，且加入第n个点后依然可以被半圆周覆盖\(α_n\)的期望为

$E(α_n)=α_{n-1}\frac{α_{n-1}}{2Π-α_{n-1}}+\frac{Π+α_{n-1}}{2}\frac{2(Π-α_{n-1})}{2Π-α_{n-1}}=\frac{Π^2}{2Π-α_{n-1}}$

由数学归纳法可知，\(E(α_n)=\frac{n-1}{n}\)             ②

如果记事件在圆周上独立地随机选取n个点，这n个点可以被半圆周覆盖为事件\(X_n\)

由①和②可知

$P(X_n|P_{n-1})=\frac{2Π-α_{n-1}}{2Π}=\frac{n}{2(n-1)}$

当n=2时，显然P(X2)=1。

当n=3时，我们很容易得到P(X3)=3/4。

通过数学归纳法，我们可以得到\(P(X_n)=\frac{n}{2^{n-1}}\)