[multiset][贪心]NOIP2018 TG T1 赛道修建

题目描述

C 城将要举办一系列的赛车比赛。在比赛前，需要在城内修建 m 条赛道。

C 城一共有 nn 个路口，这些路口编号为1,2,…,n，有 n−1 条适合于修建赛道的双向通行的道路，每条道路连接着两个路口。其中，第 i 条道路连接的两个路口编号为 ai​ 和 bi​，该道路的长度为 li​。借助这 n−1 条道路，从任何一个路口出发都能到达其他所有的路口。

一条赛道是一组互不相同的道路 e1​,e2​,…,ek​，满足可以从某个路口出发，依次经过 道路 e1​,e2​,…,ek​（每条道路经过一次，不允许调头）到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全，要求每条道路至多被一条赛道经过。

目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案，使得修建的 mm 条赛道中长度最小的赛道长度最大（即 m 条赛道中最短赛道的长度尽可能大）

输入输出格式

输入格式：

 

输入文件第一行包含两个由空格分隔的正整数 n,m，分别表示路口数及需要修建的 赛道数。

接下来 n-1 行，第 ii 行包含三个正整数 ai​,bi​,li​，表示第 i 条适合于修建赛道的道 路连接的两个路口编号及道路长度。保证任意两个路口均可通过这 n−1 条道路相互到达。每行中相邻两数之间均由一个空格分隔。

 

输出格式：

 

输出共一行，包含一个整数，表示长度最小的赛道长度的最大值。

 

输入输出样例

输入样例#1：

7 1 
1 2 10 
1 3 5 
2 4 9 
2 5 8 
3 6 6 
3 7 7

输出样例#1：

31

输入样例#2： 

9 3 
1 2 6 
2 3 3 
3 4 5 
4 5 10 
6 2 4 
7 2 9 
8 4 7 
9 4 4

输出样例#2：

15

说明

【输入输出样例 1 说明】

所有路口及适合于修建赛道的道路如下图所示：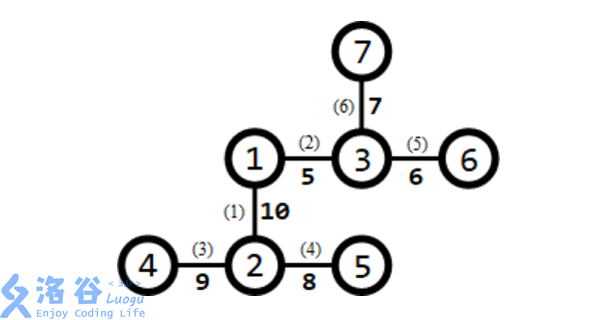

道路旁括号内的数字表示道路的编号，非括号内的数字表示道路长度。 需要修建 1 条赛道。可以修建经过第 3,1,2,6 条道路的赛道（从路口 4 到路口 7）， 则该赛道的长度为 9 + 10 + 5 + 7 = 31，为所有方案中的最大值。

【输入输出样例 2 说明】

所有路口及适合于修建赛道的道路如下图所示：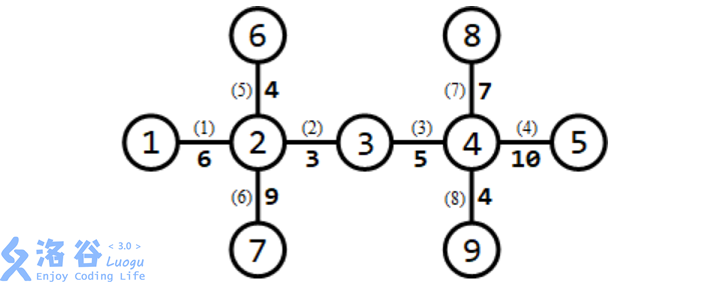

需要修建 3条赛道。可以修建如下 3条赛道：

1. 经过第 1,6条道路的赛道（从路口 1 到路口7），长度为 6 + 9 = 15；
2. 经过第5,2,3,8 条道路的赛道（从路口6 到路口 9），长度为 4 + 3 + 5 + 4 = 16；
3. 经过第 7,4 条道路的赛道（从路口 8 到路口5），长度为 7 + 10 = 17。 长度最小的赛道长度为 15，为所有方案中的最大值。

【数据规模与约定】

所有测试数据的范围和特点如下表所示 :

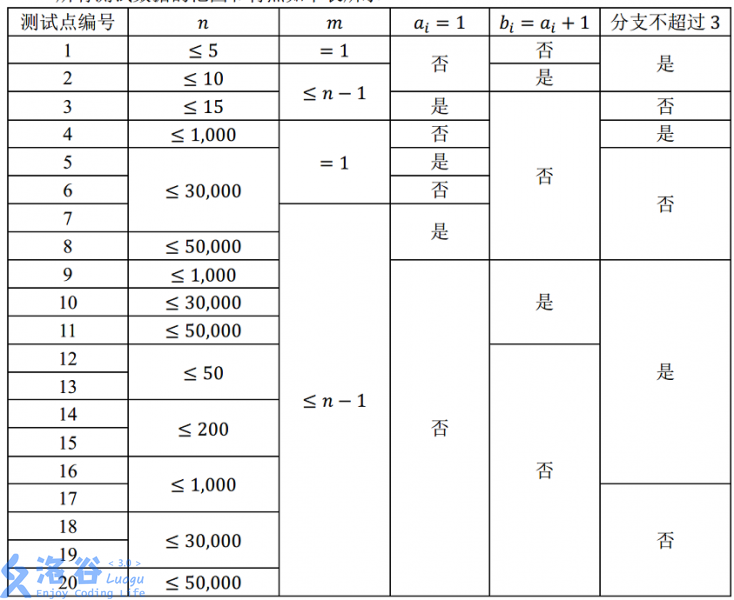
其中，“分支不超过 3”的含义为：每个路口至多有 3 条道路与其相连。 对于所有的数据， 2 ≤ n ≤ 50,000， 1 ≤ m ≤ n-1， 1≤ai​,bi​≤n，1≤li​≤10,000。

 

分析

其实这道题挺简单的（果然是我太菜了吗……）

二分长度应该都想得到，毕竟最小值最大，二分性不说了

首先我们可以证明，如果从i出发有两条链，它们的值大于等于length的话，那么合并它们必定不亏

为什么呢？因为这其中最多上传一条，也就是至多贡献1的答案，那么显然合并会更加优秀

那么我们可以用f[i]表示从i出发向下所得到未被占用的最长链，那么我们用multiset存所有能够上传到当前点的链，即f[son]+w[edge]

那么首先我们先将已经满足要求的挑出来，答案++

然后我们从小到大枚举链，用lowerbound找到最合适的链和它匹配掉，如果找不到合适的链，那么可以将这条链记录为f[i]（反正链长在multiset里面是单调的）

然后记得清空multiset，还有multiset和储存不能和子节点一起进行，要遍历完子节点才能储存链（因为共用一个嘛）

 

#include <iostream>
#include <cstdio>
#include <set>
using namespace std;
const int N=5e4+10;
struct Edge {
    int u,v,w,nx;
}g[2*N];
int cnt,list[N];
int f[N];
multiset<int> t;
int n,m,lans,ans,length;

void Add(int u,int v,int w) {
    g[++cnt]=(Edge){u,v,w,list[u]};list[u]=cnt;
}

void DFS(int u,int fa) {
    for (int i=list[u];i;i=g[i].nx)
        if(g[i].v!=fa) DFS(g[i].v,u);
    for (int i=list[u];i;i=g[i].nx)
        if(g[i].v!=fa) t.insert(g[i].w+f[g[i].v]);
    while (!t.empty()) {
        int ed=*t.rbegin();
        if (ed>=length) lans++,t.erase(t.find(ed));
        else break;
    }
    f[u]=0;
    while (!t.empty()) {
        int bg=*t.begin();t.erase(t.begin());
        multiset<int>::iterator nx=t.lower_bound(length-bg);
        if (nx==t.end()) f[u]=bg;
        else t.erase(nx),lans++;
    }
    t.clear();
}

bool Check(int x) {
    lans=0;length=x;
    DFS(1,0);
    return lans>=m;
}

int main() {
    scanf("%d%d",&n,&m);
    int l=2147483647,r=0;
    for (int i=1,u,v,w;i<n;i++) scanf("%d%d%d",&u,&v,&w),Add(u,v,w),Add(v,u,w),l=min(l,w),r+=w;
    int mid;
    while (l<=r) {
        mid=l+r>>1;
        if (Check(mid)) ans=mid,l=mid+1;
        else r=mid-1;
    }
    printf("%d",ans);
}