背包问题

一、01背包

01背包在《算法竞赛入门经典》这本书里其实已经讲的很透彻了，不多说，看图。

 

二、完全背包

重点要说一下完全背包，完全背包不限制物品数量，题目可参考leetcode322零钱兑换。

首先，可考虑通过一个二维数组进行状态转移，j列遍历钱的数目，i列遍历零钱，由于零钱不限制数量，因此可以多次添加。并且可以在当前阶段(i)添加，而不必在上一阶段(i-1)(倒序的话为i+1)的基础上进行添加。

class Solution {
    public int coinChange(int[] coins, int amount) {
        int dp[][] = new int[coins.length+1][amount+1];    
        for(int i=0;i<coins.length+1;i++){
            Arrays.fill(dp[i], amount+1);
            dp[i][0]=0;
        }
        for(int i=1;i<=coins.length;i++){
            for(int j=1;j<=amount;j++){
                if(j>=coins[i-1]){
                //    dp[i][j]=Math.min( dp[i][j-coins[i-1]]+1, dp[i-1][j-coins[i-1]]+1);
                dp[i][j]=Math.min( dp[i][j-coins[i-1]]+1, dp[i-1][j]);
                }
                else{
                   dp[i][j]=dp[i-1][j]; 
                }
                //dp[i][j]=Math.min(dp[i][j],dp[i-1][j]);
            }
        }
        return dp[coins.length][amount]>amount?-1:dp[coins.length][amount];
    }
}

考虑用滚动数据优化。

class Solution {
    public int coinChange(int[] coins, int amount) {
        int len = coins.length;
        int[] res = new int[amount+1];
        Arrays.fill(res, amount+1);
        res[0]=0;
        for(int i=0;i<len;i++){
            for(int j=1;j<=amount;j++){
                if(j>=coins[i]){
                    res[j] = Math.min(res[j],res[j-coins[i]]+1);
                }
            }
        }
        return res[amount]<amount+1?res[amount]:-1;
    }
}

三、正序逆序问题

很明显的是，01背包的滚动数组解法需要逆序遍历，而完全背包的解法则是用的正序遍历。

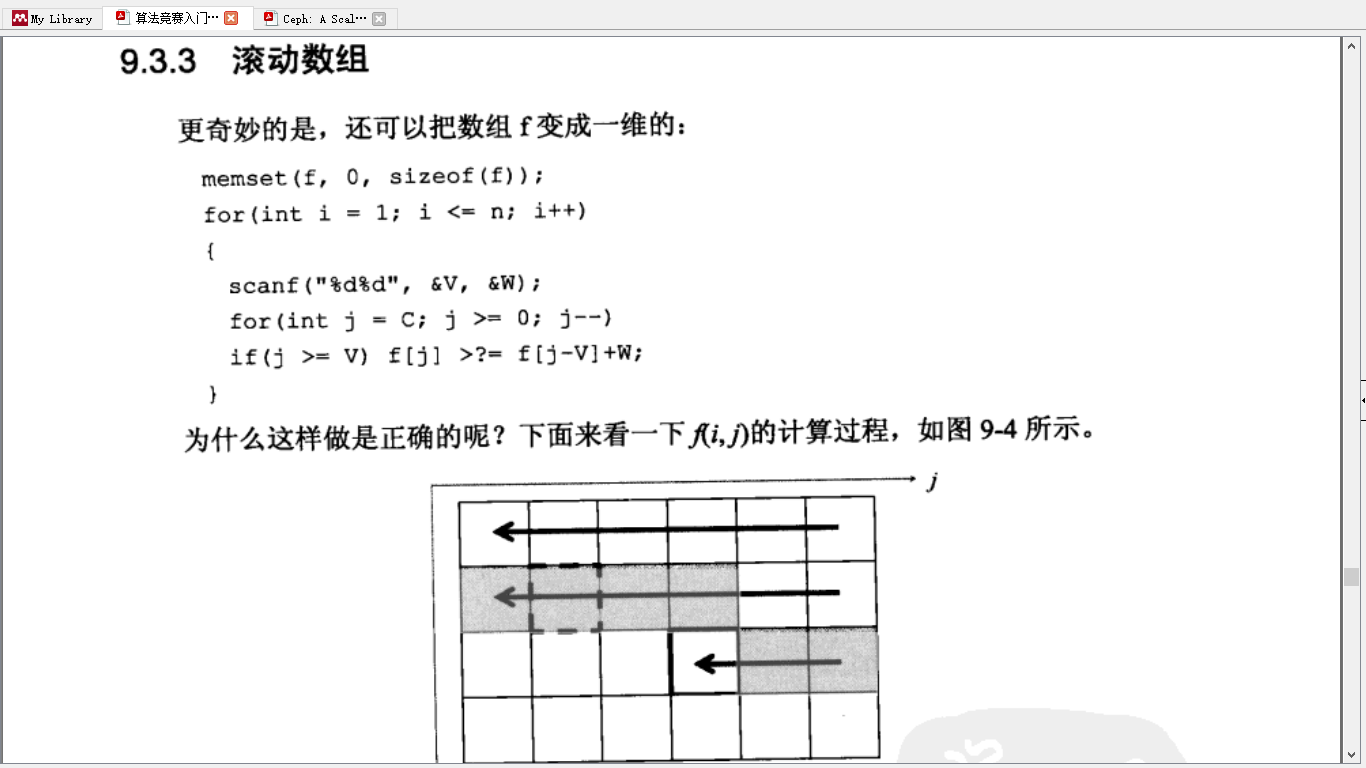
首先说为什么01背包需要逆序遍历，这个在《算法竞赛入门经典》里同样有讲，因为使用滚动数组之后，f[j]中保存的是f(i-1,j)的值，实际上是把f(i)行与f(i-1)行压缩到了一起。那么，

f[j-v]+W，实际上求的是i-1阶段的f[j-v]+W的值，此时f[j-v]的下标是i-1，而不是i。所以使用逆序，可以保证f[j-v]仍然是i-1阶段的值。如果正序，则会首先计算f[j-v]再计算f[j]，然后计算f[j]时，f[j-v]的值已经被覆盖掉了。

 

那么，为什么完全背包不担心覆盖问题呢，看一下代码。

if(j>=coins[i-1]){
      dp[i][j]=Math.min( dp[i][j-coins[i-1]]+1, dp[i-1][j]);
}else{
      dp[i][j]=dp[i-1][j]
｝

dp[i][j]的值依赖于当前行的dp[i][j-coins[i-1]]，并不是依赖于上一行的dp[i-1][j-coins[i-1]]，所以不用担心dp[i-1][j-coins[i-1]]的值被覆盖掉。而dp[i-1][j]的值在计算dp[i][j]之前就被获取过了，也不用担心被覆盖，所以可以正序计算。