图的连通性

无向图的双连通分量

1. 概念

  设G=(V,E)是连通的无向图，如果V中顶点a是一个关节点，若V中有顶点v,w使得v,w,a各不相同且v和w之间的每条路都包含a。换言之，如果删除a和与之相邻的所有边时，就会把图的一个连通分量拆分成多个连通分量。

  而若对V中每个不同的三元组v,w,a，在v和w之间都存在一条不包含a的路径，则说G是双连通的。因此，仅当一个连通的无向图没有关节点时，它才是双连通的。

  边e1和e2等价，若e1=e2或者有一条环路既包含e1又包含e2则称边e1和e2是等价的。

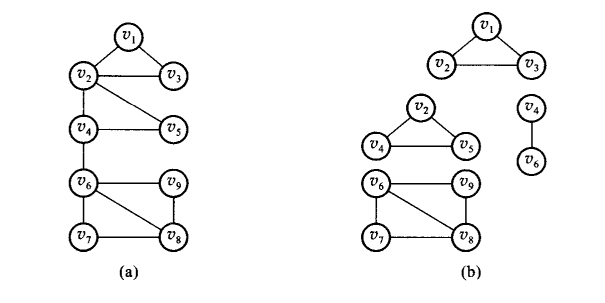
  假设Vi是Ei中各边都彼此连接的顶点集(或者利用边的等价性来划分等价类)，则每个图Gi=(Vi,Ei)叫做G的一个双连通分量。

• 双连通分量是双连通的
• 对所有的i,j(不相等)，Vi和Vj最多一起包含一个顶点
• 当且仅当v是Vi和Vj共同包含的顶点时，v是G的一个关节点

2. 求关节点

  假设对连通无向图G进行深度优先搜索和深度优先编号，产生深度优先生成树S=(V,T)和回退边B。

性质：如果一个顶点v的真子孙的所有回退边都指向v或者比v更深层次(离树根更远)的顶点，则v是关节点。若有的回退边指向v的真祖先，则v不是关节点。

算法步骤：

• 对图进行深度优先搜索，计算每个顶点v的深度优先编号dfn[v],形成深度优先生成树
• 计算所有顶点v的low[v]编号是在深度优先生成树上按后根遍历顺序进行的。low[v]取下述三值的最小者：
  • dfn[v]
  • dfn[w]：存在回退边(v,w)的任何顶点w
  • low[y]：y是v的任意儿子
• 计算完low编号后，求关节点，根据性质，可知：
  • 树根只要有2个或更多的儿子，它就是关节点，显然
  • 非树根顶点v是关节点，当且仅当v有某个儿子y，使low[y] >= dfn[v]，这里其实就是说其真子孙的回退边都指向v或者比v更深层次的顶点

代码如下：

    Biconnected_Component(G) 
    {
        T = empty;
        count = 1;
        for(all in V)
            mark v "new"
        SerachB(v0); //建立以v0为根的深度优先搜索生成树
    }
    
    SearchB(v)
    {
        mark v "old";
        dfn[v] = count;
        count ++;
        low[v] = dfn[v];
        for(each w in L[v]) {
            if(w is marked "new") {
                add (v,w) to T;
                father[w] = v;
                SearchB(w);
                if(low[w] > dfn[v])
                    A biconnected component has been found
                low[v] = min(low[v],low[w]);
            } else if(w is not father[v])
                low[v] = min(low[v],low[w]);
        }
    }

有向图的强连通分量

  有向图的一个强连通分量是该图中顶点的一个最大子集：其中的任意两个顶点x和y，存在x到y的路径，也存在y到x的路径。

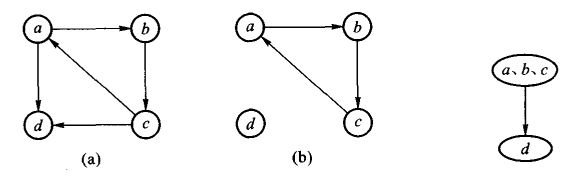
  令G=(V,E)是一个有向图，将V分割成若干等价类Vi(l<=i<=r)，使得Vi中的v和w等价的充要条件是有一条路径从v到w，也存在一条路径从w到v。令Ei(l<=i<=r)是头、尾均在Vi的边集，则Gi=(Vi,Ei)是G的强连通分量，简称强分量。把只具有一个强分量的有向图称为强连通图。

  连接两个强分量的边叫做分支横边。通过构造G的归约图 ，可以展示各强分量间的联系。归约图中每个强分量用一个顶点表示，显然，归约图中不存在环路。

Kosaraju算法步骤：

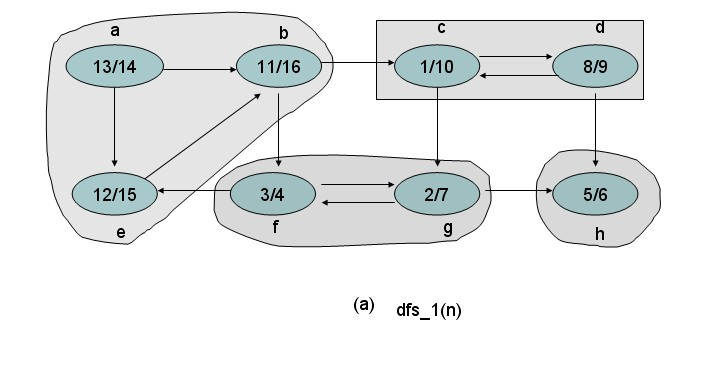
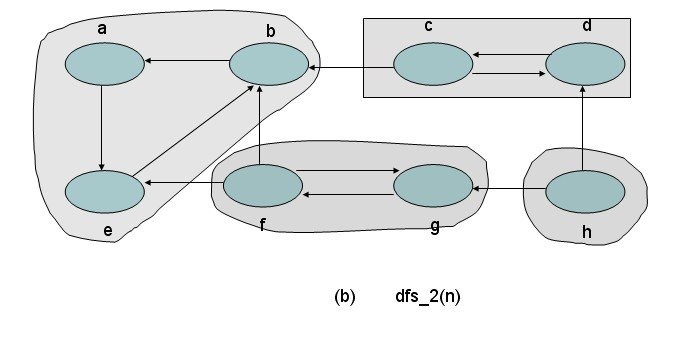
• 对有向图G进行深度优先搜索并且对顶点进行逆编号(即记录它们的离开时间)
• 将G中的每条边取反方向，构造一个新有向图Gr
• 根据前面的编号，从编号最大的顶点开始对G，进行一次深度优先搜索，凡是能到达的所有顶点，都形成一棵深度优先搜索树；若本次搜索没有到达所有顶点，从图中删除这些顶点及相连的边，继续重复该动作
• 在Gr的深度优先森林中，每棵树对应G的一个强连通分量