图的表示

  很多问题上，都可以借助图的理论来求解。图的概念，性质，实现，遍历等等都是极为重要的。这篇博客便是简单的介绍一下图如何用代码实现。

1. 基本定义

  一个图G=(V,E)是由一个非空的有限顶点集V和一个边集E所组成的二元组。

  若E中的每条边都是顶点的有序对(v,w)，则称该图为有向图。此时，v叫做(v,w)的弧尾，而w叫做(v,w)的弧头。还有一种说法是，w邻接于v。

  在无向图中，顶点v的度是关联于该顶点的边的数目，或与该顶点相邻的顶点数目，记为D(v)。在无向图中，则把以v为弧尾的弧的数目为出度，记为OD(v)，以v为弧头的弧的数目为入度，记为ID(v)，D(v) = ID(v) + OD(v)。

  无论是在有向图还是无向图中，顶点数n、边数e和度数之间的关系如下：
    

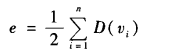
  一条简单路径指的是该路径上所有边和所有顶点，除第一个顶点和最后一个顶点可能相同外，其他都不同。假设路径为(v1,v2),(v2,v3),...,(v_n-1,v_n)，则长度为n-1(边的数量)。第一个顶点和最后一个顶点相同，则为环路，有向图的环路长度至少为1，无向图至少为3。

  在一个图所对应的无向图中，如果任意两个顶点之间都存在一条路，则称此图为连通图。在一个有向图中，如果任意两个顶点x和y之间都存在一条x到y的有向路，也存在y到x的有向路，称此图为强连通图。

2. 抽象操作

操作 | 解释

• | -
  NewNode(G,v) | 向图G中添加一个新的顶点v
  DelNode(G,v) | 删除顶点v及和它相连的边
  SetSucc(G,v1,v2) | 建立一条边(v1,v2)
  DelSucc(G,v1,v2) | 删除边(v1,v2)
  Succ(G,v) | 返回顶点v出度对应的顶点集合，即直接后继顶点序列
  Pre(G,v) | 返回顶点v入度对应的顶点集合，即直接前导顶点序列
  IsEdge(G,v1,v2) | 如果存在(v1,v2)，返回TRUE

3. 图的表示

3.1 邻接矩阵

  设G=(V,E),V={0,1,...,n-1}，则表示G的邻接矩阵A是其元素按下式定义的nxn矩阵：
    

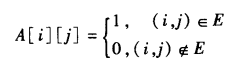
  明显，这是一种空间换取时间的表示方法，A[i][j]上也不一定放0或者1，也可以在特定情况下放边上的标记信息。

3.2 邻接表

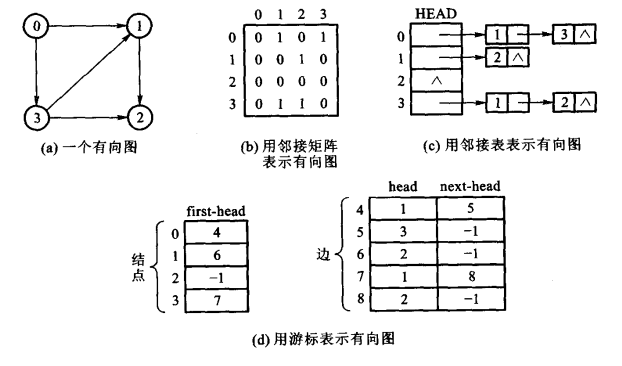
  用数组HEAD[i]表示G的顶点i。对于E中的每条边(i,j)，用一个带链的结点表示，并以HEAD[i]为表头结点将所有这种结点链接起来，称为关于顶点i的邻接表。

  此外，还可以用游标来表示邻接图。设i是顶点的编号，则0<=i<=|V|-1；设j代表边的编号，则|V|<=j<=|v|+|E|-1。顶点编号i是从顶点i发出的第一条边的尾，而first_head[i]=j是该边的编号，该边的头可通过head[j]求得；next_head[j]=k是以i为尾的第二条边的编号，第二条边的头可由head[k]求得；接着next_head[k]求得第三条边...

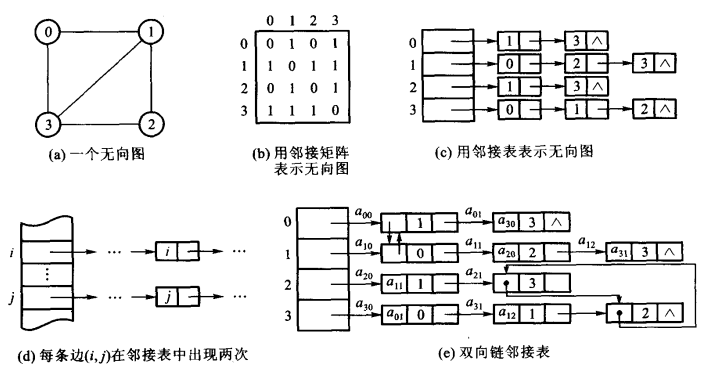
  一些情况下，无向图也可以表示成双链。

  有向图：

  无向图：

邻接矩阵所需空间为|V|²，邻接表所需空间为|V|+|E|，因此当|V|+|E|<<|V|²时，常用邻接表。