B树

1. 定义

B树是一种平衡搜索树，但是在降低磁盘I/O操作数方面要做的更好一些，许多数据库也是使用B树或者B树的变体来存储信息。

一棵B树T是具有以下性质的有根树(根为T.root)

• 每个结点x有以下属性：
  • x.n，当前存储在结点x中的关键字个数
  • x.n个关键字本身x.key₁,x.key₂,...,x.key_x.n，以非降序存放，使得x.key₁ <= x.key₂ <= ... <= x.key_x.n
  • x.leaf，一个布尔值，如果x是叶结点，则为TRUE；如果x是内部结点，则为FALSE
• 每个内部结点x还包含x.n+1个指向其孩子的指针x.c₁，x.c₂,...,x.c_x.n+1。叶结点没有孩子
• 关键字x.key_i对存储在各子树中的关键字范围加以分割；如果k_i为任意一个存储在以x.c_i为根的子树中的关键字，那么
    k₁ <= x.key₁ <= k₂ <= x.key₂ <= ... <= x.key_x.n <= k_x.n+1
• 每个叶结点具有相同的深度，即树的高度h
• 每个叶结点所包含的关键字个数有上界和下界。用一个被称为B树的最小度数的固定整数t>=2来表示这些界
  • 除了根结点以外的每个结点必须至少有t-1个关键字。因此，除了根结点以外的每个内部结点至少有t个孩子。如果树非空，根结点至少有一个关键字
  • 每个结点至多可以包含2t-1个关键字。因此，一个内部结点至多可有2t个孩子。当一个结点恰好有2t-1个关键字时，称该结点是满的

t = 2时的B树是最简单的。每个内部结点右2个、3个或者4个孩子，即一棵2-3-4树。然而在实际中，t的值越大，B树的高度就越小

2. 搜索B树

  假设B树的根结点始终在主存中，这样就无需对根做DISK_READ操作，但是当根结点被改变时，要对其做DISK_WRITE操作。任何被当做参数的结点被传递之前，都要对它们进行一次DISK_READ操作。

  搜索一棵B树和搜索一棵二叉搜索树很相似，只是在每个结点所做的不是二叉或者“两路”分支选择，二是一个(x,n+1)路的分支选择。

    //搜索某个根结点为x子树关键字为k的指针
    B_TREE_SEARCH(x,k)
    {
        i = 1;
        while i <= x.n and k > x.keyi
            i = i + 1;
        if i<= x.n and k == x.key
            return (x,i)
        elsif x.leaf
            return NIL;
        else
            DISK_READ(x,ci);
            return B_TREE_SEARCH(x.ci,k);
    }

3. 创建空的B树

    B_TREE_CREATE(T)
    {
        x = ALLOCATE_NODE();
        x.leaf = TRUE;
        x.n = 0;
        DISK_WRITE(x);
        T.root = x;
    }

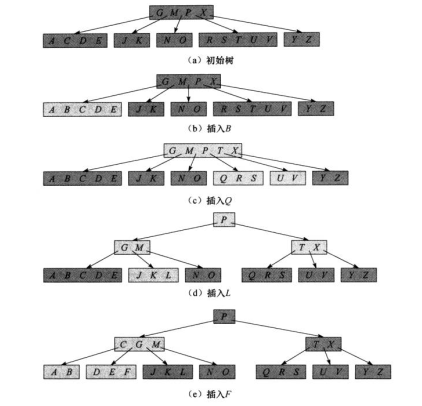
4. 插入操作

  在插入过程中，固然会因为很多情况而破坏B树的性质，故引进分裂的概念。对于一个满的结点，插入新结点必然会破坏性质，所以插入前将该结点分裂成两半，每边T-1个结点，中间的一个跑到父结点上。如图：

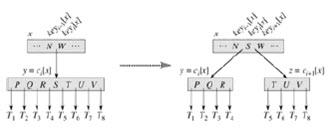
    //给出的参数表示x的第i个子结点是满的
    B_TREE_SPLIT_CHILD(x,i)
    {
        z = ALLOCATE_NODE();
        y = x.ci;
        z.leaf = y.leaf;
        z.n = t-1;
        for j = 1 to t-1
            z.keyj = y.keyj+t
        if not y.leaf
            for j = 1 to t
                z.cj = y.cj+t;
        y.n = t-1;
        for j = x.n+1 downto i+1
            x.cj+1 = x.cj;
        x.ci+1 = z;
        x.n = x.n+1;
        DISK_WRITE(y);
        DISK_WRITE(z);
        DISK_WRITE(x);
    }

  在一棵高度为h的B树T中，以沿树单程下行方式插入一个关键字k的操作需要O(h)次磁盘存取

    B_TREE_INSERT(T,k)
    {
        r = T.root;
        if r.n == 2t-1
            s = ALLOCATE_NODE();
            T.root = s;
            s.leaf = FALSE;
            s.n = 0;
            s.c1 = r;
            B_TREE_SPLIT_CHILD(s,1);
            B_TREE_INSERT_NONFULL(s,k);
        else
            B_TREE_INSERT_NONFULL(r,k);
    }
    
    
    B_TREE_INSERT_NONFULL(x,k)
    {
        i = x.n;
        if x.leaf
            while i >= 1 and k < x.key
                x.keyi+1 = x.keyi;
                i = i - 1;
            x.keyi+1 = k;
            x.n = x.n + 1;
            DISK_WRITE(x);
        else
            while i >= 1 and k < x.key
                i = i - 1;
            i = i + 1;
            DISK_READ(x,ci);
            if x.ci.n == 2t-1
                B_TREE_SPLIT_CHILD(x,i);
                if k > x.keyi
                    i = i + 1;
            B_TREE_INSERT_NONFULL(x.ci,k);
    }
    

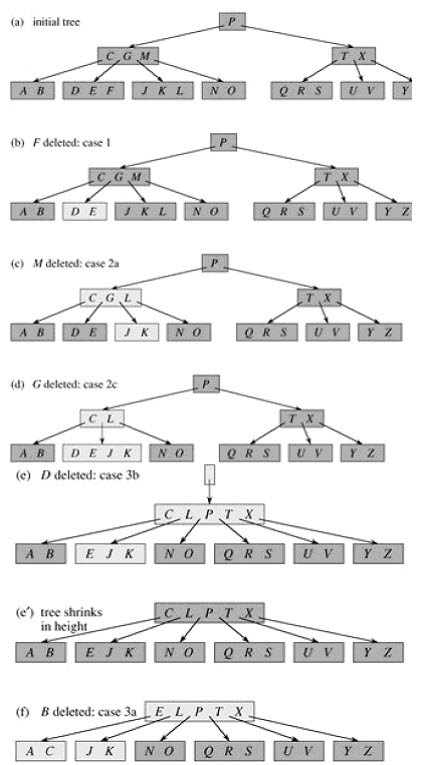
5. 删除操作

删除规则：

• 如果关键字k在结点x中，并且x是叶结点，则从x中删除k
• 如果关键字k在结点x中，并且x是内部结点，则做以下操作：
  • 如果结点x中前于k的子结点y至少包括t个关键字，则找出k在以y为根的子树中的前驱k'。递归地删除k'，并在x中用k'代替k
  • 对称地，如果y有少于t个关键字，则检查结点x中后于k的子结点z。如果z至少有t个关键字，则找出k在以z为根的子树中的后继k'。递归地删除k'，并在x中用k'代替k
  • 否则，如果y和z都只包含t-1个关键字，则将k和z的全部合并进y，这样x就失去了k和指向z的指针，并且y现在包含2t-1个关键字。然后释放z并递归地从y中删除k
• 如果关键字k当前不在内部结点x中，则确定必包含k的子树的根x.ci。如果x.ci只有t-1个关键字，必须执行步骤3a或3b来保证降至一个至少包含t个关键字的结点，然后通过对x的某个合适的子结点进行递归而结束
  • 如果x.ci只含有t-1个关键字，但是它的一个相邻的兄弟至少包含t个关键字，则将x中某个关键字降至x.ci中，将x.ci的的相邻左兄弟或右兄弟的一个关键字升至x，将该兄弟中相应的孩子指针移至x.ci中，这样就使得x.ci增加了一个额外的关键字
  • 如果x.ci以及x.ci的所有相邻兄弟都只包含t-1关键字，则将x.ci与一个兄弟合并，即将x的一个关键字移至新合并的结点，使之成为该结点的中间关键字