红黑树
1. 概念
红黑树是一棵二叉查找树,它在每个结点上增加了一个存储为来表示结点的颜色,可以RED或BLACK。通过对任意一条从根到叶子的简单路径上各个结点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出2倍,因而是近似于平衡。
树中每个结点都包含5个属性:color、key、left、right和p。如果一个结点没有子结点或者父结点,则该结点相应指针属性值为NIL,视为外结点一样的叶子结点。
2. 性质
每一棵红黑树都需要满足下面的性质:
- 每个结点或是红色的,或是黑色的
- 根结点是黑色的
- 每个叶结点(NIL)是黑色的
- 如果一个结点是红色的,则它的两个子结点都是黑色的
- 对每个结点,从该结点到其所有后代叶子结点的简单路径上,均包含相同数目的黑色结点
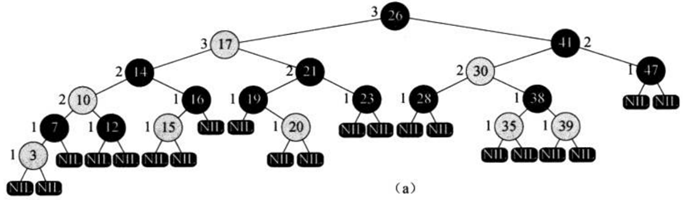
为了方便和节省空间,经常在红黑树T中设置一个属性T.nil,然后所有结点的空指针指向其:
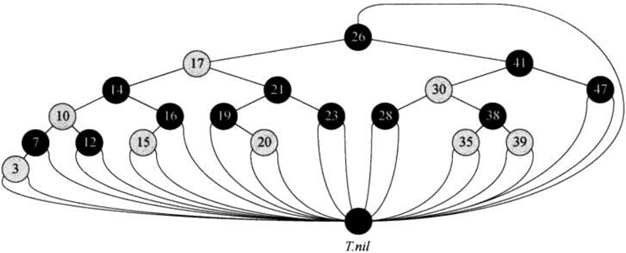
从某个结点x出发(不含该结点)到达一个叶结点的任意一条简单路径上的黑色结点个数称为该结点的黑高,记为bh(x)。
一棵有n个内部结点的红黑树的高度至多为2lg(n+1),这保证了其查找操作都在O(lgn)内能完成
3. 旋转
在插入和删除操作后,红黑树的性质可能会被破坏,这时候就要通过旋转来进行调整。旋转分为2种:左旋和右旋。当在某个结点x上左左旋时,x右孩子不为T.nil结点,则左旋后,x成为y的左孩子,y的左孩子成为x的右孩子。右旋一样的道理。
一棵红黑树包括两个结点:
struct RBT {
node * root;
node * nil;
};

- 代码如下:
LEFT_ROTATE(T,x)
{
y = x.right;
x.right = y.left;
if y.left != T.nil
y.left.p = x;
y.p = x.p;
if x.p == T.nil
T.root = y;
elsif x == x.p.left
x.p.left = y;
else
x.p.right = y;
y.left = x;
x.p = y;
}
//RIGHT_ROTATE类似
4. 插入
讲道理插入原理和二叉查找树差不多,只不过多了一个维护性质的过程。
- 代码如下
RB_INSERT(T,z)
{
y = T.nil;
x = T.root;
while x != T.nil {
y = x;
if z.key < x.key
x = x.left;
else
x = x.right;
}
z.p = y;
if y == T.nil
T.root = z;
elsif z.key < y.left
y.left = z;
else
y.right = z;
z.left = T.nil;
z.right = T.nil;
z.color = RED;
RB_INSERT_FIXUP(T,z);
}
RB_INSERT_FIXUP(T,z)
{
while z.p.color == RED {
if z.p == x.p.p.left {
y = z.p.p.right;
if y.color == RED { //case 1
z.p.color = BLACK;
y.color = BLACK;
z.p.p.color = RED;
z = z.p.p;
} elsif z == z.p.right { //case 2
z = z.p;
LEFT_ROTATE(T,z);
}
z.p.color = BLACK; //case 3
z.p.p.color = RED;
RIGHT_ROTATE(T,z.p.p);
} else
//直接是上个代码left<->right调换即可
}
T.root.color = BLACK;
}
其实有6种情况可以改变红黑树的性质,但是由于是对称的,所以只给了一边的代码,具体情况图示:
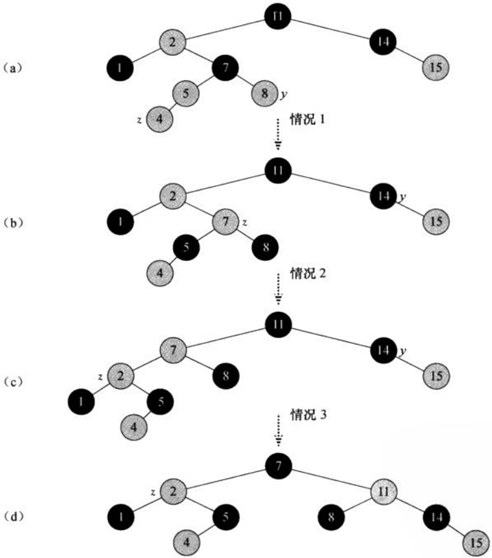
5. 删除
删除其实和查找二叉树的删除类似,只是多了一个维护性质的过程,先贴出代码:
//v为根的子树替换u为根的子树
RB_TRANSPLANT(T,u,v)
{
if u.p == T.nil
T.root = v;
elsif u == u.p.left
u.p.left = v;
else
u.p.right = v;
v.p = u.p;
}
RB_DELETE(T,z)
{
y = z;
y_original_color = y.color;
if z.left == T.nil
x = z.right;
RB_TRANSPLANT(T,z,z.right);
elsif z.right == T.nil
x = z.left;
RB_TRANSPLANT(T,z,z.left);
else
y = TREE_MINIMUM(z.right);
y_original_color = y.color;
x = y.right;
if y.p == z
x.p = y;
else
RB_TRANSPLANT(T,y,y.right);
y.right = z.right;
y.right.p = y;
RB_TRANSPLANT(T,z,y);
y.left = z.left;
y.left.p = y;
y.color = z.color;
//只有颜色为黑才会破坏性质
if y_original_color == BLACK
RE_DELETE_FIXUP(T,x);
}
RB_DELETE_FIXUP(T,x)
{
while x != T.root and x.color == BLACK
{
if x== z.p.left
w = x.p.right;
if w.color == RED //case 1
w.color = BLACK;
x.p.color = RED;
LEFT_ROTATE(T,x.p);
w = x.p.right;
if w.left.color == BLACK and w.right.color == BLACK //case 2
w.color = RED;
x = x.p;
eleif w.right.color == BLACK //case 3
w.left.color = BLACK;
w.color = RED;
RIGHT_ROTATE(T,w);
w = x.p.right;
w.color = x.p.right; // case 4
x.p.color = BLACK;
w.right.color = BLACK;
LEFT_ROTATE(T,x.p);
x = T.root;
else
//和上面一样,将left互换right
}
}
有8种情况,但是是对称的,所以只给出4种情况的代码,具体看图:
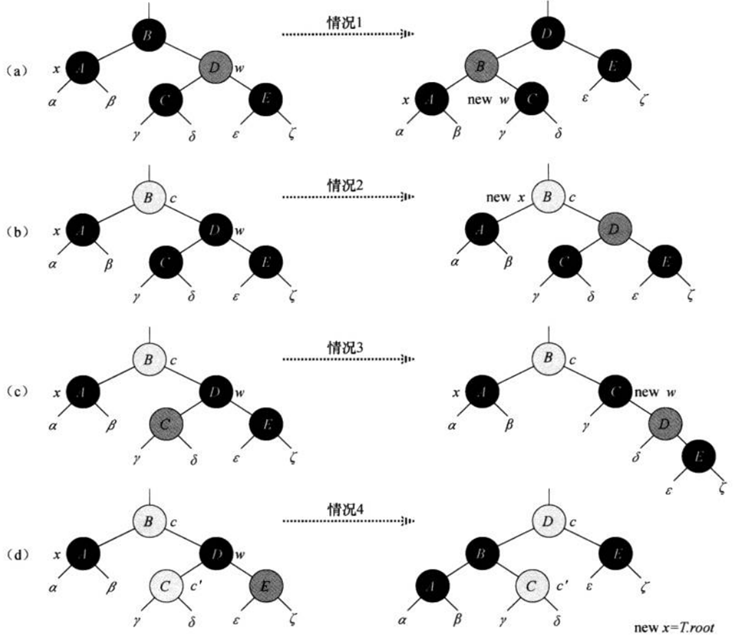
作者: vachester
出处:http://www.cnblogs.com/vachester/
邮箱:xcchester@gmail.com
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接,否则保留追究法律责任的权利。

