跳表
参考了这篇博客,再加上自己的理解,总结了跳表的一些知识。
1. 概念
基于并联的链表,跳表是一种随机化的数据结构,在插入、删除、查找的复杂性都是O(logN)。它是链表的一种,只不过加入了跳跃功能,正是因为这个特性,使得它的查找复杂度是O(logN)。
跳表是平衡树的一种替代的数据结构,但是和红黑树不相同的是,跳表对于树的平衡的实现是基于一种随机化的算法的,这样也就是说跳表的插入和删除的工作是比较简单的。
2. 实现原理
跳表采用的是“空间换取时间”的原理
先从链表开始,如果是一个简单的链表,那么我们知道在链表中查找一个元素I的话,需要将整个链表遍历一次。

如果是说链表是排序的,并且节点中还存储了指向前面第二个节点的指针的话,那么在查找一个节点时,仅仅需要遍历N/2个节点即可。

- 基本实现
- 一个跳表应该有几个层(level)组成
- 第一层包含所有的元素
- 每一层都是一个有序的链表
- 如果x出现在第i层,则所有比i小的层都包含x
- 每个结点包含key及其对应的value和一个指向同一层链表的下个结点的指针数组

3. 代码实现
- 先定义每个结点的指针:
typedef struct nodeStructure *node;
typedef struct nodeStructure
{
keyType key; // key值
valueType value; // value值
// 向前指针数组,根据该节点层数的
// 不同指向不同大小的数组
node forward[1]; //柔性数组
};
- 定义跳表类型
typedef struct listStructure{
int level; /* Maximum level of the list */
struct nodeStructure * header; /* pointer to header */
} * list;
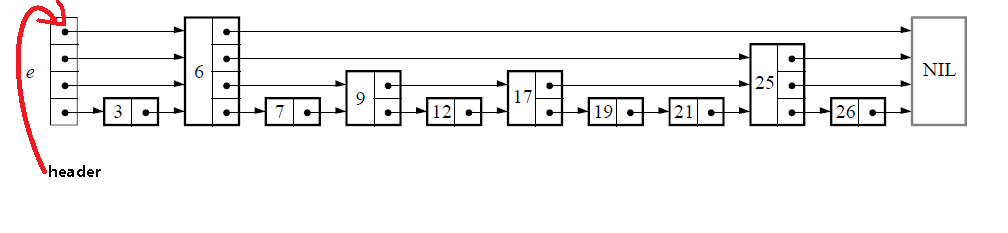
- 定义辅助变量和函数:
node NIL = nullptr;
#define MaxNumberOfLevels 16
#define MaxLevel (MaxNumberOfLevels-1)
#define newNodeOfLevel(l) (node)malloc(sizeof(struct nodeStructure)+(l)*sizeof(node *))
//插入元素的时候元素所占有的层数完全是随机算法
int randomLevel()
{
int level=1;
while (rand()%2)
level++;
return level;
}
- 初始化成红线部分
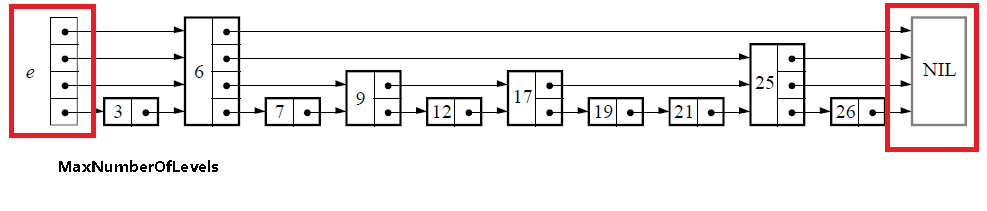
list newList()
{
list l;
int i;
// 申请list类型大小的内存
l = new listStructure;
// 设置跳表的层level,初始的层为0层(数组从0开始)
l->level = 0;
// 生成header部分
l->header = new listStrutcure;
// 将header的forward数组清空
for(i=0;i<MaxNumberOfLevels;i++) {
l->header->forward[i] = new nodeStructure;
l->header->forward[i] = NIL;
}
return l;
};
- 插入操作
由于跳表数据结构整体上是有序的,所以在插入时,需要首先查找到合适的位置,然后就是修改指针(和链表中操作类似),然后更新跳表的level变量。
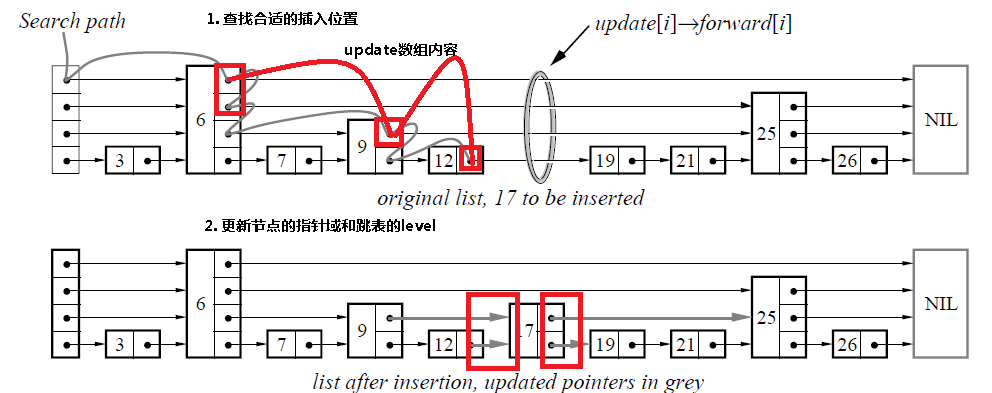
boolean insert(l,key,value)
register list l;
register keyType key;
register valueType value;
{
register int k;
// 使用了update数组
node update[MaxNumberOfLevels];
register node p,q;
p = l->header;
k = l->level;
/*******************1步*********************/
do {
// 查找插入位置
while (q = p->forward[k], q->key < key)
p = q;
// 设置update数组
update[k] = p;
} while(--k>=0); // 对于每一层进行遍历
// 这里已经查找到了合适的位置,并且update数组已经
// 填充好了元素
if (q->key == key)
{
q->value = value;
return(false);
};
// 随机生成一个层数
k = randomLevel();
if (k>l->level)
{
// 如果新生成的层数比跳表的层数大的话
// 增加整个跳表的层数
k = ++l->level;
// 在update数组中将新添加的层指向l->header
update[k] = l->header;
};
/*******************2步*********************/
// 生成层数个节点数目
q = newNodeOfLevel(k);
q->key = key;
q->value = value;
// 更新两个指针域
do
{
p = update[k];
q->forward[k] = p->forward[k];
p->forward[k] = q;
} while(--k>=0);
// 如果程序运行到这里,程序已经插入了该节点
return(true);
}
- 删除操作
和插入是相同的,首先查找需要删除的节点,如果找到了该节点的话,那么只需要更新指针域,如果跳表的level需要更新的话,进行更新。
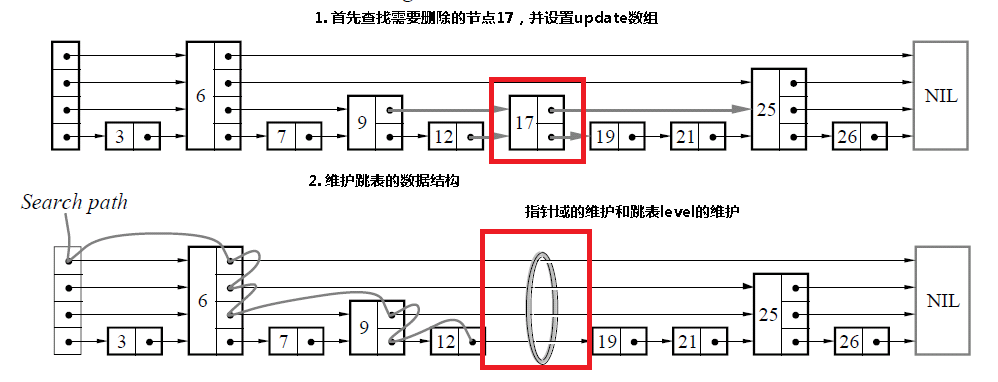
boolean delete(l,key)
register list l;
register keyType key;
{
register int k,m;
// 生成一个辅助数组update
node update[MaxNumberOfLevels];
register node p,q;
p = l->header;
k = m = l->level;
// 这里和插入部分类似,最终update中包含的是:
// 指向该节点对应层的前驱节点
do
{
while (q = p->forward[k], q->key < key)
p = q;
update[k] = p;
} while(--k>=0);
// 如果找到了该节点,才进行删除的动作
if (q->key == key)
{
// 指针运算
for(k=0; k<=m && (p=update[k])->forward[k] == q; k++)
// 这里可能修改l->header->forward数组的值的
p->forward[k] = q->forward[k];
// 释放实际内存
free(q);
// 如果删除的是最大层的节点,那么需要重新维护跳表的
// 层数level
while( l->header->forward[m] == NIL && m > 0 )
m--;
l->level = m;
return(true);
}
else
// 没有找到该节点,不进行删除动作
return(false);
}
- 查找操作
查找操作前面都提到过,特别简单
boolean search(l,key,valuePointer)
register list l;
register keyType key;
valueType * valuePointer;
{
register int k;
register node p,q;
p = l->header;
k = l->level;
do
{
while (q = p->forward[k], q->key < key)
p = q;
} while (--k>=0);
// 这里查找到的值是大于或者是等于需要查找的key值的
if (q->key != key)
return(false);
*valuePointer = q->value;
return(true);
};
作者: vachester
出处:http://www.cnblogs.com/vachester/
邮箱:xcchester@gmail.com
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接,否则保留追究法律责任的权利。


