树

1. 抽象数据型

操作 | 解释

• | -
  Parent(n,T) | 返回树T结点n的父亲
  LeftMostChild(n,T) | 返回树T结点n的最左儿子
  RightSibling(n,T) | 返回树T结点n的右兄弟
  Data(n,T) | 返回树T结点n的DATA域的值
  CreateK(v,T1,...,Tk) | 建立DATA为v并且有k个子树
  Root(T) | 返回T的根结点

2. 遍历

• 先根遍历
  • 先访问根结点
  • 然后先根遍历T1
  • . . .
  • 最后先根遍历Tk
• 中根遍历
  • 先中根遍历T1
  • 访问根结点
  • . . .
  • 中根遍历Tk
• 后根遍历
  • 后根遍历T1
  • . . .
  • 后跟遍历Tk
  • 访问根结点

先根遍历代码

    //按先根顺序列出n及其所有后代的数据域的值
    void PreOrder(node n,TREE T)
    {
        node c;
        visit(Data(n,T));
        c = LeftMostChild(n,T);
        while(c != NULL)
        {
            PreOrder(c,T);
            c = RightSibling(c,T);
        }
    }

3. 树的实现

3.1 树的数组表示

• 示意图

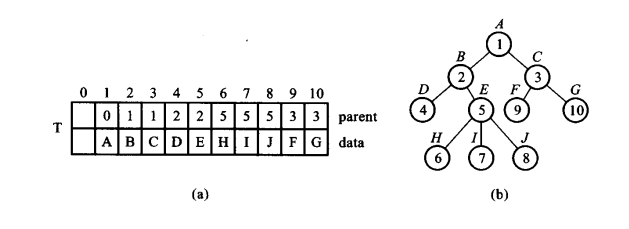
• 代码实现

    struct node {
        int parent; //记录父亲
        char data;
    };
    
    typedef node TREE[11];
    
    TREE T;
    

3.2 树的邻接表表示

• 示意图

• 代码实现

    typedef int node;
    struct celltype {
        node element;
        celltype *next;
    };
    
    typedef celltype * LIST;
    typedef celltype * position;
    
    struct TREE {
        LIST header[maxnodes];
        datatype data[maxnodes];
        node root;
    };
    

3.3 树的左右链表示

• 介绍

  每个结点都有3个域，一个是数据域，一个指向其最左子树，一个指向其右兄弟。

• 示意图

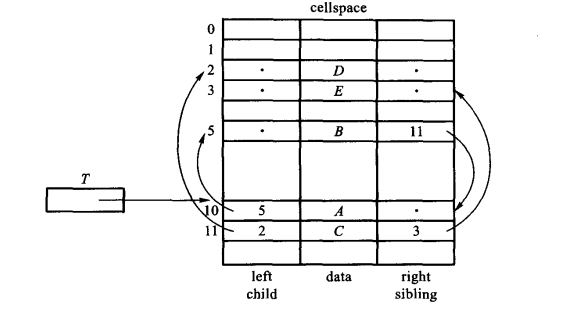
• 代码实现

    struct {
        datatype data;
        int leftchild;
        int rightsibling;
    } celltype[maxnodes];
    
    //若想快速得到parent，可以加入一个域，指向父亲
    

4. 森林和二叉树

这里我基本上是参考着这篇博客。

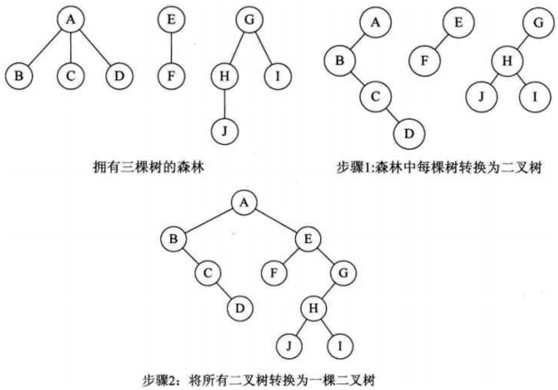
4.1 树转化为二叉树

基本步骤：

• 加线：在所有兄弟结点之间加一条连线
• 去线：除了最左汉子，删除结点与其它孩子的连线
• 层次调整：进行顺时针选装(第一个孩子是结点的左孩子，兄弟旋转后变成其右孩子)

4.2 森林转二叉树

基本步骤

• 把每一棵树转化为二叉树
• 第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子，用线连接

4.3 二叉树转树

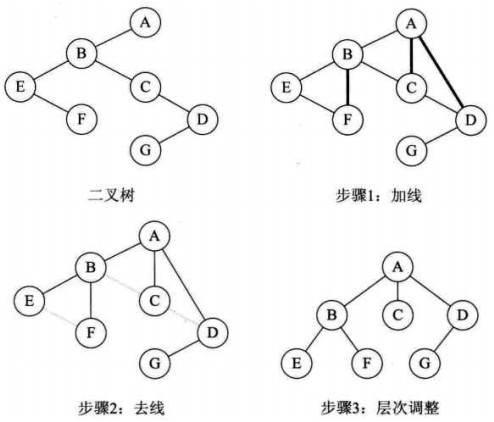
基本步骤

• 加线：若某结点X的左孩子结点存在，则将这个左孩子的右孩子结点、右孩子的右孩子结点、右孩子的右孩子的右孩子结点...，都作为结点X的孩子。将结点X与这些右孩子结点用连线连起来
• 去线：删除原二叉树中所有结点与其右孩子结点的连线
• 层次调整

4.4 二叉树转森林

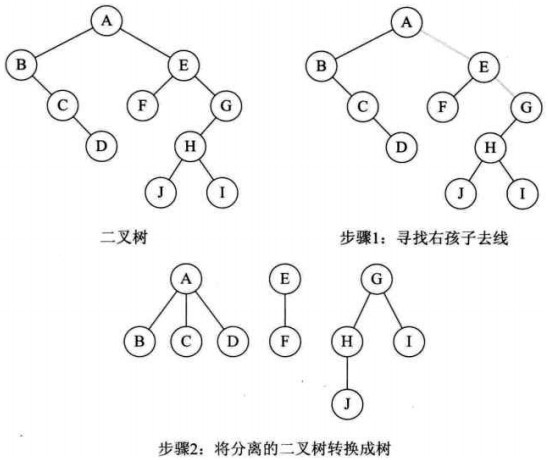
基本步骤

• 从根结点开始，若右孩子存在，则把右孩子结点的连线删除。再查看分离后的二叉树，若其根结点的右孩子存在，继续删除...
• 把每棵分离的二叉树转为树

4.5 代码实现

    #define MAX 100

    //定义树的结构
    struct Tree
    {
    	vector<Tree *> child;
    	char data;
    	Tree(){ child.clear();}
    };
    
    //定义森林，即多棵树
    typedef vector<Tree *> Forest;
    
    //定义二叉树的结构
    struct BTree
    {
    	BTree * lchild;
    	BTree * rchild;
    	char data;
    };


    //从文件里读入信息并且创建二叉树和树
    void Create_Forest(Forest & F,ifstream & in)
    {
    	string str;
    	Tree * ALL[MAX], *p = NULL;
    	int top,i,j = 0;
    	while(in >> str && str != "")
    	{
    		top = -1;
    		i = 0;
    		while(str[i] != '\0')
    		{
    			//遇到左括号，则层数加1，且下一个添加最左子树
    			if(str[i] == '(')
    			{
    				top ++;
    				ALL[top] = p;
    			}
    			//遇到右括号，则层数减1
    			else if(str[i] == ')')
    				top --;
    			//遇到逗号，且下一个添加右子树
    			else if(str[i] == ',')
    				;
    			else
    			{
    				p = new Tree;
    				p -> data = str[i];
    				if(static_cast<int>(F.size()) == j)
    					F.push_back(p);
    				else
    					ALL[top] ->child.push_back(p);
    			}
    			i ++;
    		}
    		j++;
    	}	
    }
    
    void Create_BTree(BTree * &B,ifstream & in)
    {
    	BTree *ALL[MAX],*p = NULL;
        bool judge;
    	string str;
    	in >> str;
        int top = -1, i = 0;
        B = NULL;//先将根节点置空
        while(str[i] != '\0')
        {
            //遇到左括号，则层数加1，且下一个添加左子树
            if(str[i] == '(')
            {
                top ++;
                ALL[top] = p;
                judge = true;
            }
            //遇到右括号，则层数减1
            else if(str[i] == ')')
                top --;
            //遇到逗号，且下一个添加右子树
            else if(str[i] == ',')
                judge = false;
            else
            {
                p = new BTree;
                p -> data = str[i];
                p -> lchild = NULL;
                p -> rchild = NULL;
                if(B == NULL)   
    				B = p;
                else if(judge)
                    ALL[top] -> lchild = p;
                else
                    ALL[top] -> rchild = p;
            }
            i ++;
        }
    }
    
    //将森林转化为二叉树
    BTree * Forest_to_BTree(Forest F)
    {
    	BTree *B = new BTree;
    	Tree * bt = F[0];
    	B ->data = F[0] ->data;
    	F.erase(F.begin());
    	Forest tmp;
    	for(int num = bt ->child.size(), i = 0;i < num;i++)
    		tmp.push_back(bt ->child[i]);
    	if (!tmp.empty()) B->lchild = Forest_to_BTree(tmp);
    	if (!F.empty()) B->rchild = Forest_to_BTree(F);
    	return B;
    }
    
    //将二叉树转化为一颗树
    Tree * BTree_to_Tree(BTree * B)
    {
    	Tree * T;
    	T = new Tree;
    	T ->data = B ->data;
    	BTree * tmp;
    	if(B ->lchild)
    	{
    		tmp = B ->lchild;
    		while(tmp)
    		{
    			T ->child.push_back(BTree_to_Tree(tmp));
    			tmp = tmp ->rchild;
    		}
    	}
    	return T;
    }
    
    //利用上面的算法进而将二叉树转化为森林
    Forest BTree_to_Forest(BTree * B)
    {
    	vector<BTree *> f;
    	Forest F;
    	Tree * tr;
    	BTree *tmp = B;
    	while(tmp)
    	{
    		f.push_back(tmp);
    		tmp = tmp ->rchild;
    	}	
    	for(int num = static_cast<int>(f.size()),j = 0;j < num; j++)
    	{
    		f[j] ->rchild = NULL;
    		tr = BTree_to_Tree(f[j]);
    		F.push_back(tr);
    	}
    	return F;
    }