二叉树

1. 概念

  二叉树是有限个结点的集合，这个集合或者是空集，或者由一个根节点和两棵不相交的二叉树组成，其中一棵叫做根的左子树，另一棵叫做根的右子树。

  满二叉树是高为k且有2^k - 1个结点的二叉树。

  完全二叉树是具有下述性质的二叉树：

   a. 所有叶结点都在k或者k-1层
   b. k-1层的所有叶结点都在非终结符结点的右边
   c. 只有k-1层最右非终结结点可能有一个叶子结点

2. 性质

• 性质1：在二叉树中第i层的结点数量最多为2^(i-1)
• 性质2：高度为k的二叉树其结点数最多为2^k - 1
• 性质3：如下图

3. 基本操作

操作 | 解释

• | -
  Empty(BT) | 建立一棵空的二叉树
  IsEmpty(BT) | 为空则返回TRUE
  CreateBT(v,LT,RT) | 建立新树，根值为v，另外为左右子树
  Lchild(BT) | 返回左儿子
  Rchild(BT) | 返回右儿子
  Data(BT) | 返回根节点数据预的值

4. 遍历方式

假设图如下：

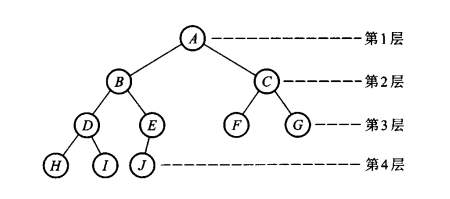
• 先根遍历：A B D H I E J C F G

• 中根遍历：H D I B J E A F C G

• 后根遍历：H I D J E B F G C A

• 给出先根遍历代码：

    void PreOrder(BTREE BT)
    {
        if(!IsEmpty(BT)) {
            visit(Data(BT));  //中根遍历放中间，后根遍历同理
            PreOrder(Lchild(BT));
            PreOrder(Rchild(BT));
        }
    }

5. 二叉树的实现

5.1 左右链表示

• 示意图：

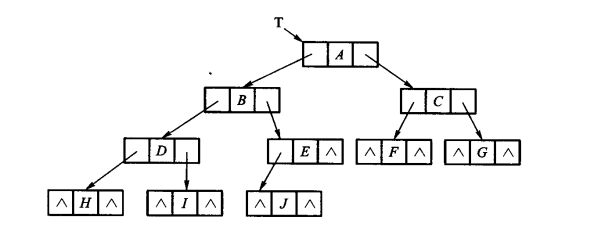
• 代码实现：

    struct node {
        node *lchild;
        datatype data;
        node *rchild;
    };
    
    typedef node * BTREE;
    
    BTREE CreateBT(datatype v, BTREE ltree, BTREE rtree)
    {
        BTREE root;
        root = new node;
        root->data = v;
        root->lchild = ltree;
        root->rchild = rchild;
        return root;
    }

5.2 游标表示

• 示意图：

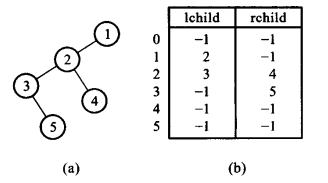
• 代码实现：

    struct {
        int lchild;
        int rchild;
    } cellspace[maxnodes];
    
    /*
        cellspace[i].lchild是结点i的左儿子，
        如果为-1，表示没有相应的儿子，
        图中可以看出
    */

5.3 线索二叉树

• 概念：在左右链的表示法中，具有n个结点的树需要2n个指针，必然会造成浪费，故利用浪费的指针指向有用的地方。

  • 当某个结点的lchild为空时，则令其指向该结点的中根遍历的前导结点
  • 若rchild为空，则指向中根遍历的后续结点

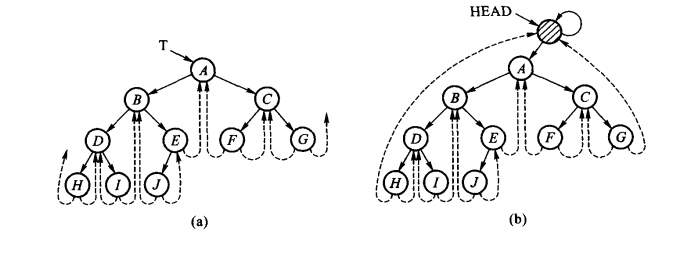
• 示意图

• 代码实现：

    struct node{
        node *lchild;
        node *rchild;
        boolean ltag;
        boolean rtag;
        infotype info;
    };    

• 规则
  • 若P的左子树为空，则令P->ltag=FALSE，且P->lchild=$P
  • 若P的左子树不为空，则令P->ltag=TRUE，且P->lchild=左子树的根
  • 若P的右子树为空，则令P->rtag=FALSE，且P->rchild=P$
  • 若P的右子树不为空，则令P->rtag=TRUE，且P->rchild=右子树的根

$P表示P在中根遍历序列中的前导结点

• 特殊情况

  线索二叉树总是由低的位置指向高的位置。在中序遍历第一个结点H和最后一个结点G，需要建立一个空结点HEAD，让它们的指针指向其，如下：

    HEAD->lchild = T; //T是指向根结点的指针
    HEAD->rchild = HEAD;
    HEAD->ltag = TRUE;
    HEAD->rtag = TRUE;
    
    //空二叉树则为：
    HEAD->lchild = HEAD;
    HEAD->ltag = FALSE;
    HEAD->rchild = HEAD;
    HEAD->rtag = TRUE;
    

线索二叉树在对于“给定P,求$P或者P$时特别容易”

5.4 完全二叉树的数组表示法

• 示意图

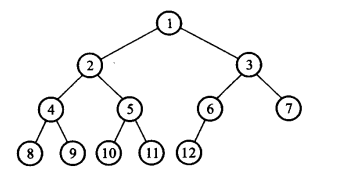
• 规则
  • 若i != 1，则其父亲结点是⌊i/2⌋
  • 若i == 1，则i是根结点
  • 若2i <= n，则左儿子是2i，若2i > n，则i无左儿子
  • 若2i+1 <= n，则右儿子是2i+1，若2i+1 > n，则无右儿子

部分资料来自《数据结构与算法--张岩》