记忆化搜索的应用
记忆化搜索的应用
一般来说,动态规划总要遍历所有的状态,而搜索可以排除一些无效状态。更重要的是搜索还可以剪枝,可能剪去大量不必要的状态,因此在空间开销上往往比动态规划要低很多。
如何协调好动态规划的高效率与高消费之间的矛盾呢?有一种折中的办法就是记忆化算法。记忆化算法在求解的时候还是按着自顶向下的顺序,每求解一个状态,就将它的解保存下来,以后再次遇到这个状态的时候,就不必重新求解了。这种方法综合了搜索和动态规划两方面的优点,因而还是很有使用价值的。
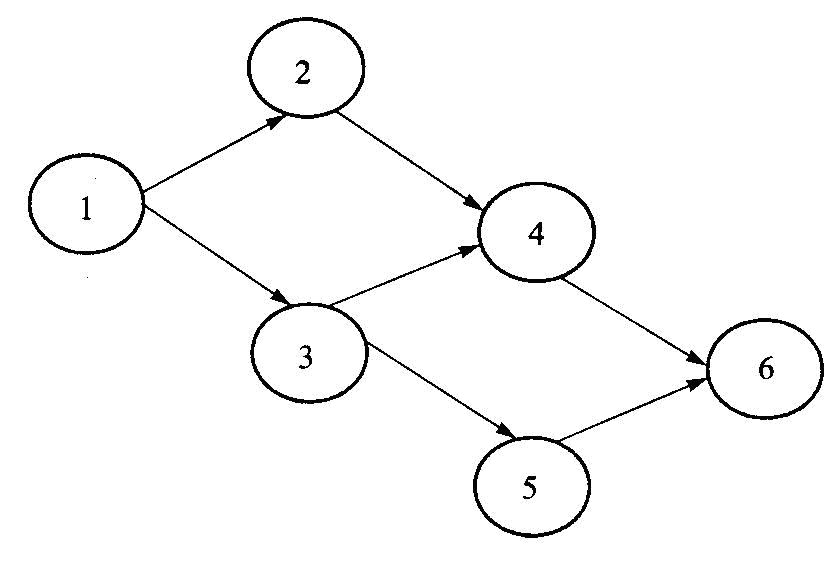
举一个例子:如右图所示是一个有向无环图,求从顶点1到顶点6的最长路径。(规定边的方向从左到右)
我们将从起点(顶点1)开始到某个顶点的最长路径作为状态,用一维数组opt记录。Opt[j]表示由起点到顶点j时的最长路径。显然,opt[1]=0,这是初始状态,即动态规划的边界条件。于是,我们很容易地写出状态转移方程式:opt[j]=max{opt[k]+a[k,j]}(k到j有一条长度为a[k,j]的边)。虽然有了完整的状态转移方程式,但是还是不知道动态规划的顺序。所以,还需要先进行一下拓扑排序,按照排序的顺序推下去,opt[6]就是问题的解。
可以看出,动态规划相比搜索之所以高效,是因为它将所有的状态都保存了下来。当遇到重复子问题时,它不像搜索那样把这个状态的最优值再计算一遍,只要把那个状态的最优值调出来就可以了。例如,当计算opt[4]和opt[5]时,都用到了opt[3]的值。因为已经将它保存下来了,所以就没有必要再去搜索了。
但是动态规划仍然是有缺点的。一个很突出的缺点就是要进行拓扑排序。这道题的拓扑关系是很简单的,但有些题的拓扑关系是很复杂的。对于这些题目,如果也进行拓扑排序,工作量非常大。遇到这种情况,我们可以用记忆化搜索的方法,避免拓扑排序。
【例】滑雪
【问题描述】
小明喜欢滑雪,因为滑雪的确很刺激,可是为了获得速度,滑的区域必须向下倾斜,当小明滑到坡底,不得不再次走上坡或等着直升机来载他,小明想知道在一个区域中最长的滑坡。滑坡的长度由滑过点的个数来计算,区域由一个二维数组给出,数组的每个数字代表点的高度。下面是一个例子:
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度减小,在上面的例子中,一条可行的滑坡为25-24-17-16-1(从25开始到1结束),当然25-24……2…1更长,事实上这是最长的一条。
【输入格式】
输入的第一行为表示区域的二维数组的行数R和列数C(1≤R、C≤100),下面是R行,每行有C个数代表高度。
【输出格式】
输出区域中最长的滑坡长度。
【输入样例】ski.in
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
【输出样例】ski.out
25
【算法分析】
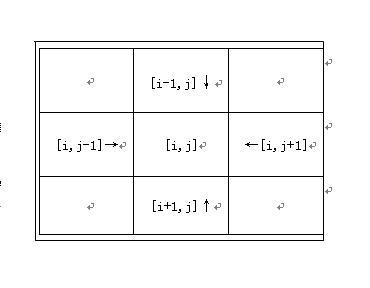
由于一个人可以从某个点滑向上下左右相邻四个点之一,如上图所示。当且仅当高度减小,对于任意一个点[i,j],当它的高度小于与之相邻的四个点([i-1,j], [i,j+1], [i+1,j], [i,j-1])的高度时,这四个点可以滑向[i,j],用f[i,j]表示到[i,j]为止的最大长度,则f[i,j]=max{f(i+a,j+b)}+1,其中坐标增量{(a,b)=[(1,0),(-1,0),(0,1),(0,-1)],0<i+a<=r,0<j+b<=c,High[i,j]<High[i+a,j+b]}。为了保证满足条件的f[i+a,j+b]在f[i,j]前算出,需要对高度排一次序,然后从大到小规划(高度)。最后再比较一下所有f(i,j){0<i≤r,0<j≤c},找出其中最长的一条路线。我们还可以用记忆化搜索的方法,它的优点是不需进行排序,按照行的顺序,利用递归逐点求出区域中到达此点的最长路径,每个点的最长路径只求一次。
1 const
2 dx:array[1..4] of shortint=(0,-1,0,1); {x的坐标增量}
3 dy:array[1..4] of shortint=(-1,0,1,0); {y的坐标增量}
4 var
5 r,c,ans,anss:longint;
6 map,f:array[1..100,1..100] of longint;
7 procedure init;
8 var i,j:longint;
9 begin
10 readln(r,c);
11 for i:=1 to r do
12 for j:=1 to c do
13 read(map[i,j]); {读入每个点的高度}
14 ans:=0; anss:=0;
15 fillchar(f,sizeof(f),0);
16 end;
17 function search(x,y:longint):longint; {函数的作用是求到[x,y]点的最长路径}
18 var i,j,nx,ny,tmp,t:longint;
19 begin
20 if f[x,y]>0 then {此点长度已经求出,不必进行进一步递归,保证每一个点的最大长度只求一次,这是记忆化搜索的特点}
21 begin
22 search:=f[x,y]; exit;
23 end;
24 t:=1;
25 for i:=1 to 4 do {从四个方向上搜索能达到[x,y]的点}
26 begin
27 nx:=x+dx[i]; ny:=y+dy[i]; {新坐标}
28 if (1<=nx)and(nx<=r) and (1<=ny)and(ny<=c) {边界限制}
29 and (map[nx,ny]>map[x,y]) {高度比较}
30 then
31 begin
32 tmp:=search(nx,ny)+1; {递归进行记忆化搜索}
33 if tmp>t then t:=tmp;
34 end;
35 end;
36 f[x,y]:=t;
37 search:=t;
38 end;
39 procedure doit;
40 var i,j:longint;
41 begin
42 for i:=1 to r do {按照行的顺序,利用递归逐点求出区域中到达此点的最长路径}
43 for j:=1 to c do
44 begin
45 anss:=search(i,j);
46 //f[i,j]:=anss;
47 if anss>ans then ans:=anss; {寻找最大长度值}
48 end;
49 end;
50 procedure outit;
51 var i,j:longint;
52 begin
53 {for i:=1 to r do begin
54 for j:=1 to c do
55 write(f[i,j],' '); writeln; end;}
56 writeln(ans);
57 end;
58 begin
59 init;
60 doit;
61 outit;
62 end.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号