笔算开方法
笔算开方
笔算开平方法,用这个方法可以求出任何正数的算术平方根。
(并非是近似值,而是精确值)
原理:
方法可简记为——二十倍初商加试商
预备:

下面具体来讲一下计算步骤:
-
以小数点为起点,将被开方数的整数部分和小数部分分别以2位为一组分隔(整数从右往左分,小数从左往右分,不足则用0补齐),分成n段,则表明所求平方根是n位数
-
确定平方根的第一位:最大平方数。在不超过第一组数中取最大数x(1..9),将x作为除数和第一组的商,求出开方余项(第一组余数+第二组)
-
再求平方根第二位:假设第二位为a,取算式
![]() 估计出a的最大值(此为试商),使得
估计出a的最大值(此为试商),使得![]() 结果不大于开方余项。新的除数与新商得出乘积,算出新的余数
结果不大于开方余项。新的除数与新商得出乘积,算出新的余数 -
把下一组数补齐到新余数后,重复步骤3
-
小数点对齐,运算至所需精度
这样讲述显得苍白无力(有一个大概印象即可),我们直接看例子:
例如对105625进行开方:

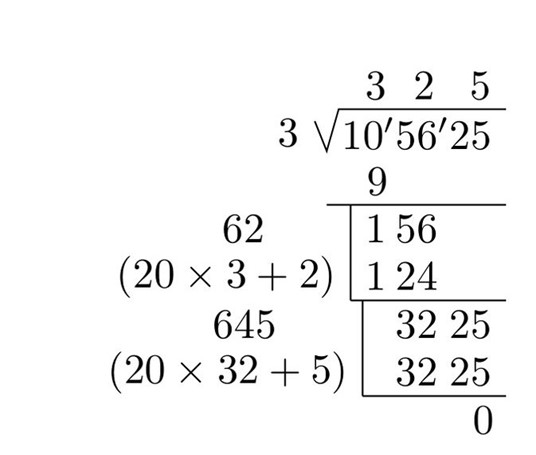
首先对105625进行分段,从右往左每两位数字分为1段,也就是10,56,25三段数字。先算出平方根的第一位数字,在平方不超过10的数字里取最大的,比如1的平方为1,2的平方为4,3的平方为9,4的平方为16,16已经超过10了,1,2,3的平方都比10小,那平方根首位数字取3,因为 1,2,3当中3最大
10-3的平方=1,将被开方数第二段数字补上去,得到156。现在算平方根第二位数字。假设这第二位数字为a,取算式a*(20*3+a),式子中20是一个固定不变的数(不论被开方数是多少)3就是刚刚计算出的平方根的首位数字。对a的值进行估计,使得 a*(20*3+a)不超过156。取a=1,a(20*3+a)=61,a=2时a(20*3+a)=124,a=3时 a*(20*3+a)=189,189已经超过156,所以a在1,2之间取值取最大的一个数,也就是2,平方根的第二位数字就是2了
a(20*3+a)=124,62 乘以平方根第二位数字,也就是62*2=124,156-124=32,将被开方数第三段数字补上去,得到3225,与前面类似,取算式 b(20*32+b),式子中20还是固定不变的数字,32是刚刚算出的平方根的前两位数字,对b取值,使得b(20*32+b)不超过3225,由计算 可知b=5,平方根第三位数字即为5
如果平方根还有第四位数字,或者更多,假设325后面还有第四位数字,算第四位数字时取算式 a(20*325+a),式子中的325即是已经算出的平方根的几位数字,后面算法都跟前面类似。对于被开方数是小数,分段时要注意,比如计算1.323 的平方根,它的小数位有3位,位数是奇数个,要补一个0上去,即1.3230,然后从左往右每两位数字分为一段。比如开方数是3.7478,小数位有4位数字,是偶数个位数,不用补0,可以直接分段,小数和整数的开方计算方法是一样的。
练习:

上述笔算开方方法是我们大多数人上学时课本附录给出的方法,实际中运算中太麻烦了。我们可以采取下面办法,实际计算中不怕某一步算错!!!而上面方法就不行。
比如136161这个数字,首先我们找到一个和136161的平方根比较接近的数,任选一个,比方说300到400间的任何一个数,这里选350,作为代表。 我们计算0.5*(350+136161/350)得到369.5
然后我们再计算0.5*(369.5+136161/369.5)得到369.0003,我们发现369.5和369.0003相差无几,并且,369^2末尾数字为1。我们有理由断定369^2=136161 一般来说能够开方开的尽的,用上述方法算一两次基本结果就出来了。再举个例子:计算469225的平方根。首先我们发现600^2<469225<700^2,我们可以挑选650作为第一次计算的数。即算
0.5*(650+469225/650)得到685.9。而685附近只有685^2末尾数字是5,因此685^2=469225
对于那些开方开不尽的数,用这种方法算两三次精度就很可观了,一般达到小数点后好几位。
实际中这种算法也是计算机用于开方的算法

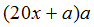 估计出a的最大值(此为试商),使得
估计出a的最大值(此为试商),使得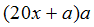 结果不大于开方余项。新的除数与新商得出乘积,算出新的余数
结果不大于开方余项。新的除数与新商得出乘积,算出新的余数 
 浙公网安备 33010602011771号
浙公网安备 33010602011771号