BFS-走迷宫

1. 题目

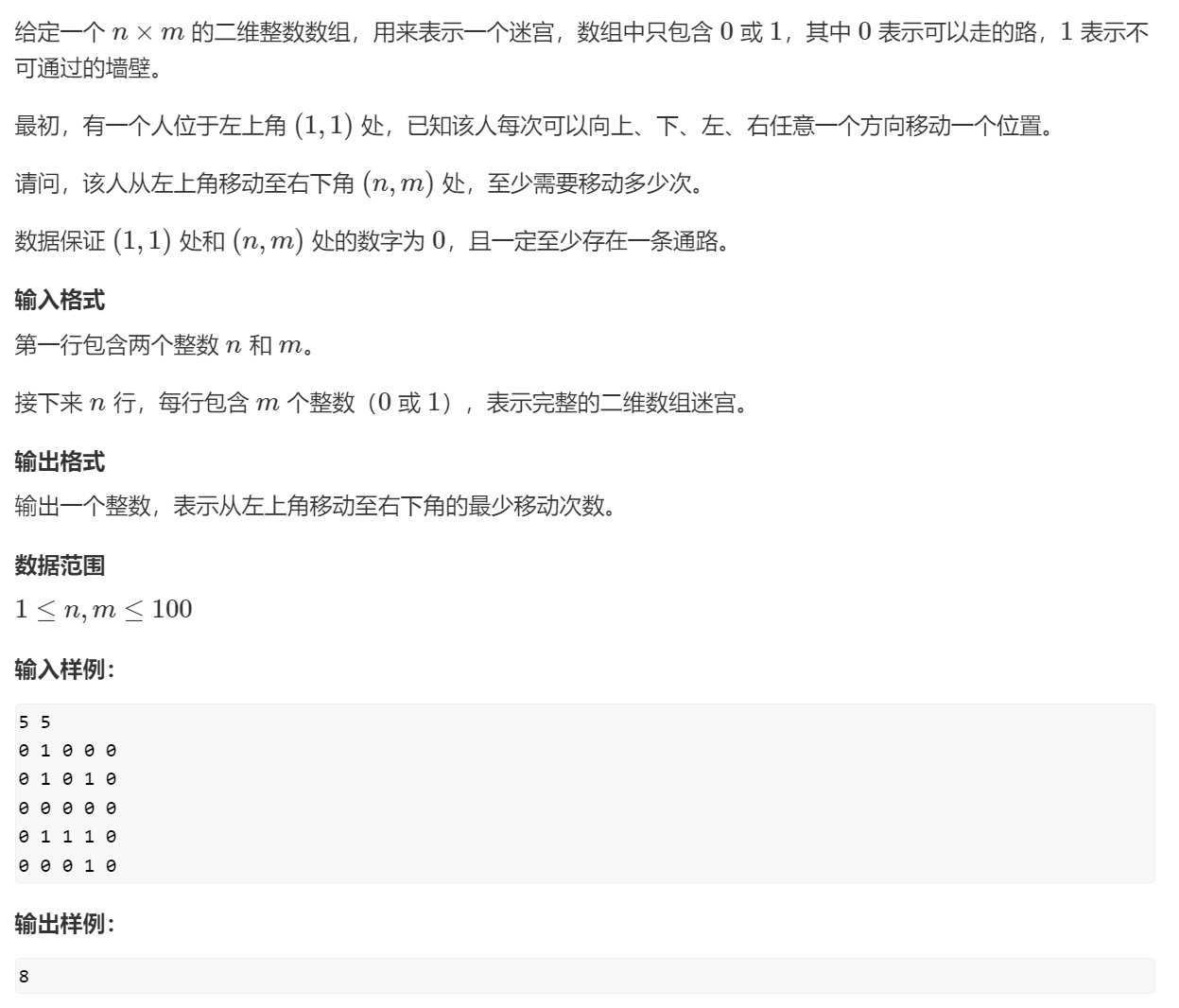
简单概述：走迷宫问题，行走的方向是上下左右。这个迷宫内有些格子不能走，想要从迷宫的左上角走到右下角，最少移动次数。这道题属于最短路问题（求出到达一个点的最短路径）。

思路分析

为什么使用BFS求到的答案能保证是最短的路径？

因为BFS是逐层搜索的，能把当前层的所有可能值包括进来，每一层的值是上一层的值加一。

更新目标状态的内容是什么？

d[x][y] = d[t.first][t.second] + 1

如何标记当然位置已经走过？

首先，d数组全部被初始化为-1。当d中的值被修改为距离起点的长度时，表示这个位置已经被走过了。

BFS 模板

代码实现

#include<iostream>
#include<queue>
#include<algorithm>
#include<cstring>
using namespace std;
 
typedef pair<int, int> PII;
 
const int N = 110;
 
int n, m;
int g[N][N], d[N][N];
queue<PII> q;
 
int bfs() {
    
    memset(d, -1, sizeof d);
    
    d[0][0] = 0;
    q.push({0, 0});
    
    while (q.size()) {
        auto t = q.front();
        q.pop();
        
        int dx[4] = {0, 1, 0, -1}, dy[4] = {1, 0, -1, 0};
        for (int i = 0; i < 4; i++) {
            int x = t.first + dx[i], y = t.second + dy[i];
            if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] != 1 && d[x][y] == -1) {
                d[x][y] = d[t.first][t.second] + 1;
                q.push({x, y});
            }
        }
    }
    return d[n - 1][m - 1];
}
 
int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
            cin >> g[i][j];
            
    cout << bfs() << endl;
    return 0;
}