正则化

我们想让我们的模型拟合训练集的数据。有时，我们用线性来模拟一些复杂的数据，就会欠拟合(underfit)，具有高偏差；这时候，我们可能就会采用一些非线性的模型拟合训练集，或许达到不错的效果；但有时，我们的模型太想拟合数据了，使得模型失去了泛化能力（泛化：能够对之前从未见过的全新示例也能给出良好的预测），具有高方差，这就是 overfit，这个结果不是我们想要的。

对于线性回归

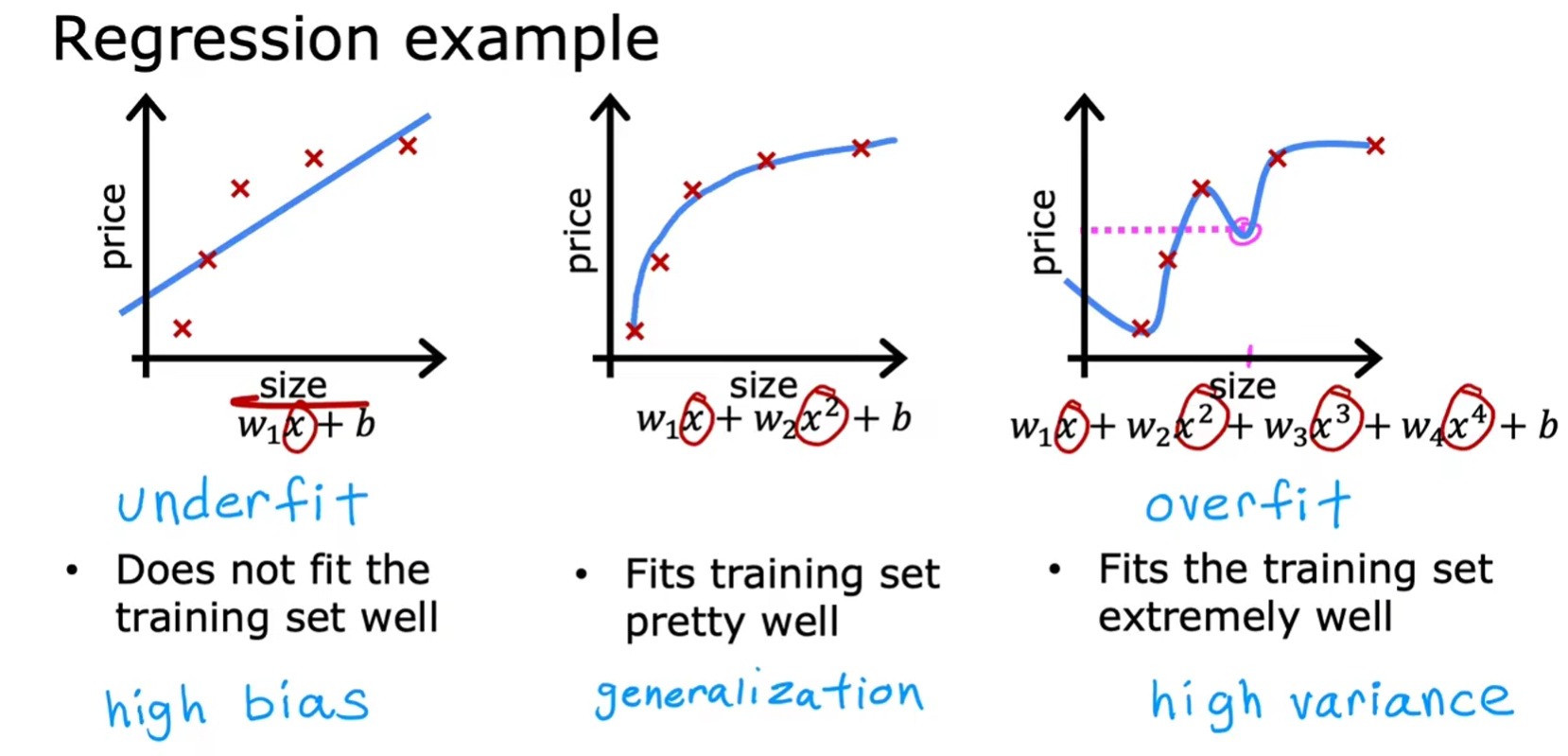
对于分类问题

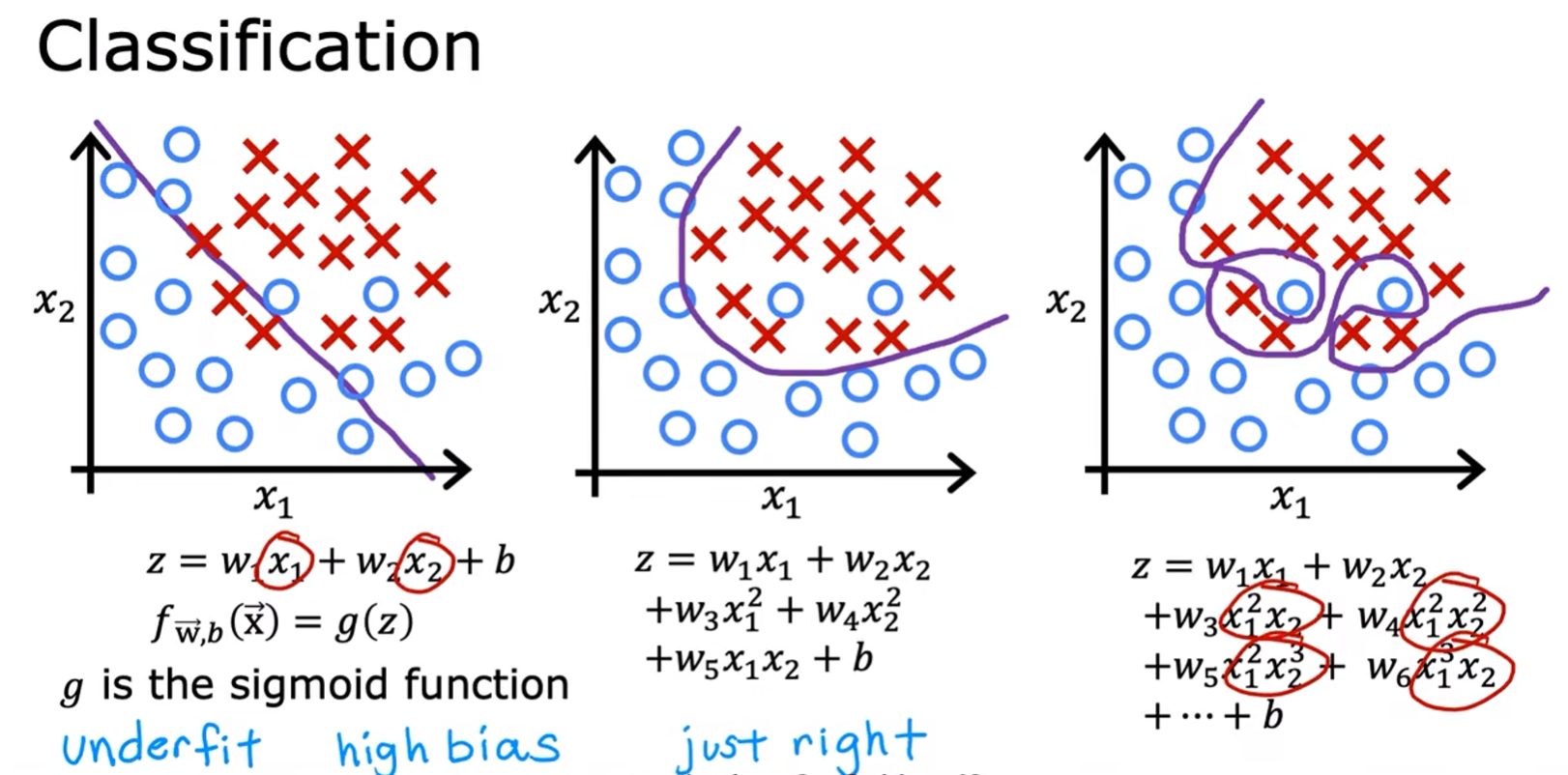
如何解决过拟合问题

1. 获取更多的数据集，扩大训练集

2. 不要用那么多的多项式特征，选择性丢掉一些特征

   通常太多的特征加上不足的数据会造成过拟合

3. 正则化 （Regularization）

正则化

正则化的提出是为了解决模型过拟合的问题。

正则化的思路：模型出现过拟合，往往是因为特征有高次幂的影响，使得一个参数的微小变化，对整体结果有较大的影响。

我们能做的是，通过通过代码函数约束 ω 的值，使得特征的参数 ω 变得较小，从而平衡特征值的影响，使得曲线更为平滑，解决过拟合的情况。

具体点就是：

1. 通过给代价函数中追加 big number * ω²的项。
2. 由于目标是 minimize J，所以，会趋向于让 ω 的值变的很小。
3. ω 变小了，回归函数中，特征的权重也就减小了，从而解决过拟合的情况

正则化线性回归

将正则化应用于线性回归，具体点就是调整线性回归代价函数和梯度下降算法

如何将正则化应用于线性回归？

1. 为代价函数添加正则化项
2. 调整梯度下降算法
3. 得到最后的正则化线性回归公式
   

正则化的原理

正则化逻辑回归

和正则化线性回归一样，先给代价函数添加正则化项，再调整梯度下降公式。并且，逻辑回归最后得到的梯度下降公式除了 f 内容不一样之外，其余和线性回归的梯度下降公式一样。