逻辑回归
逻辑回归
逻辑回归问题和线性回归问题不一样,我们将不用线性回归来解决,而使用 Sigmoid 非线性函数来处理。
🧐逻辑回归是什么?
逻辑回归并不是回归问题,是属于监督学习的一类,通常输出是几个离散值,而不是像线性回归有连续的 y。
🧐为什么不用线性回归解决逻辑回归问题?
比如说二元逻辑回归问题,输出只有 0 和 1 两种可能。线性回归对其的模拟能力很差。

逻辑回归问题不适合使用线性函数来模型,采用 Sigmoid 能更好地拟合数据
Sigmoid 函数
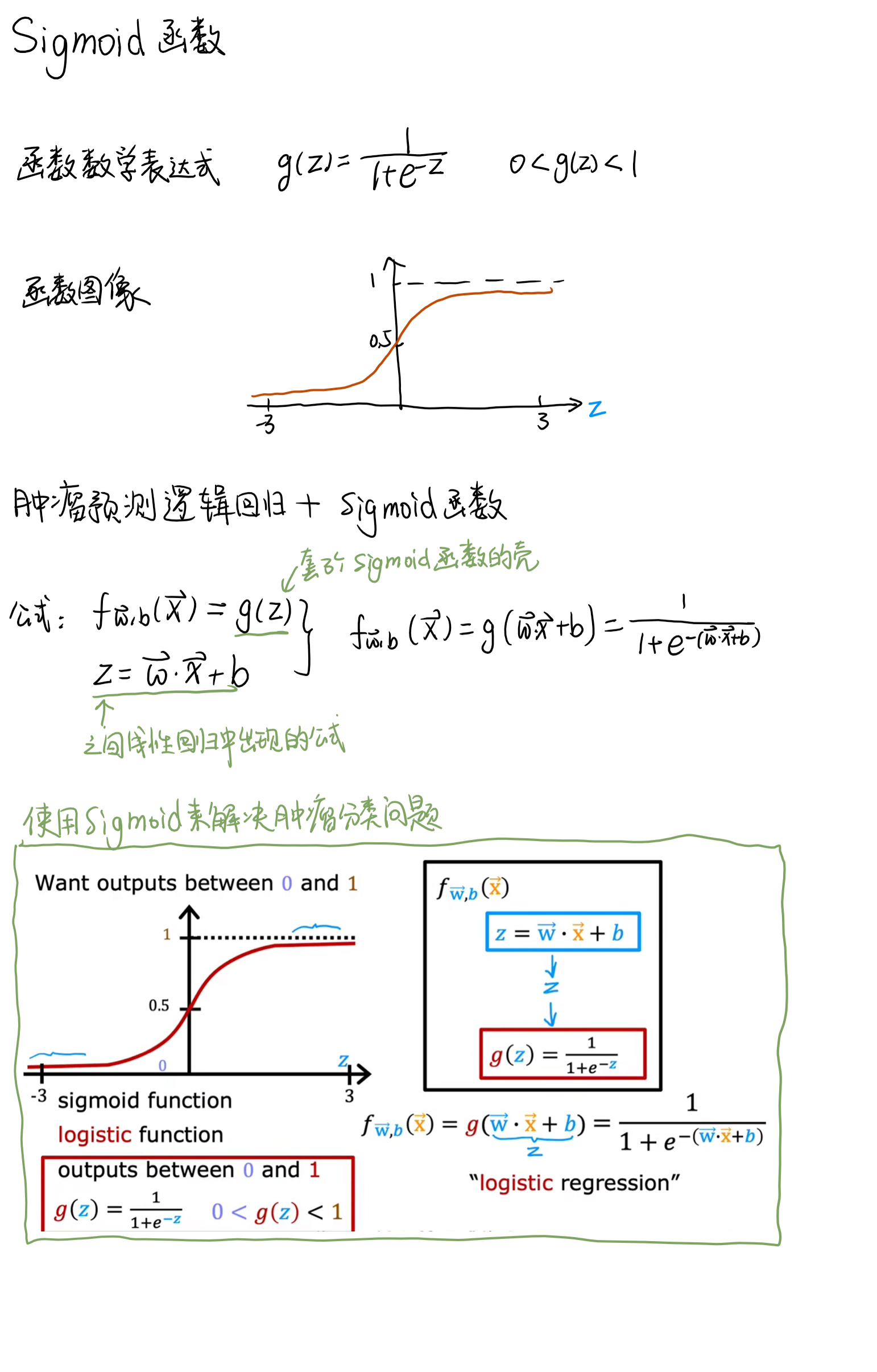
当 z 为一个线性的函数时,我们能得到一个边界,一边是 Positive,另一边是 Negative。可以通过决策边界可视化观察到一个数据应该是哪个输出。
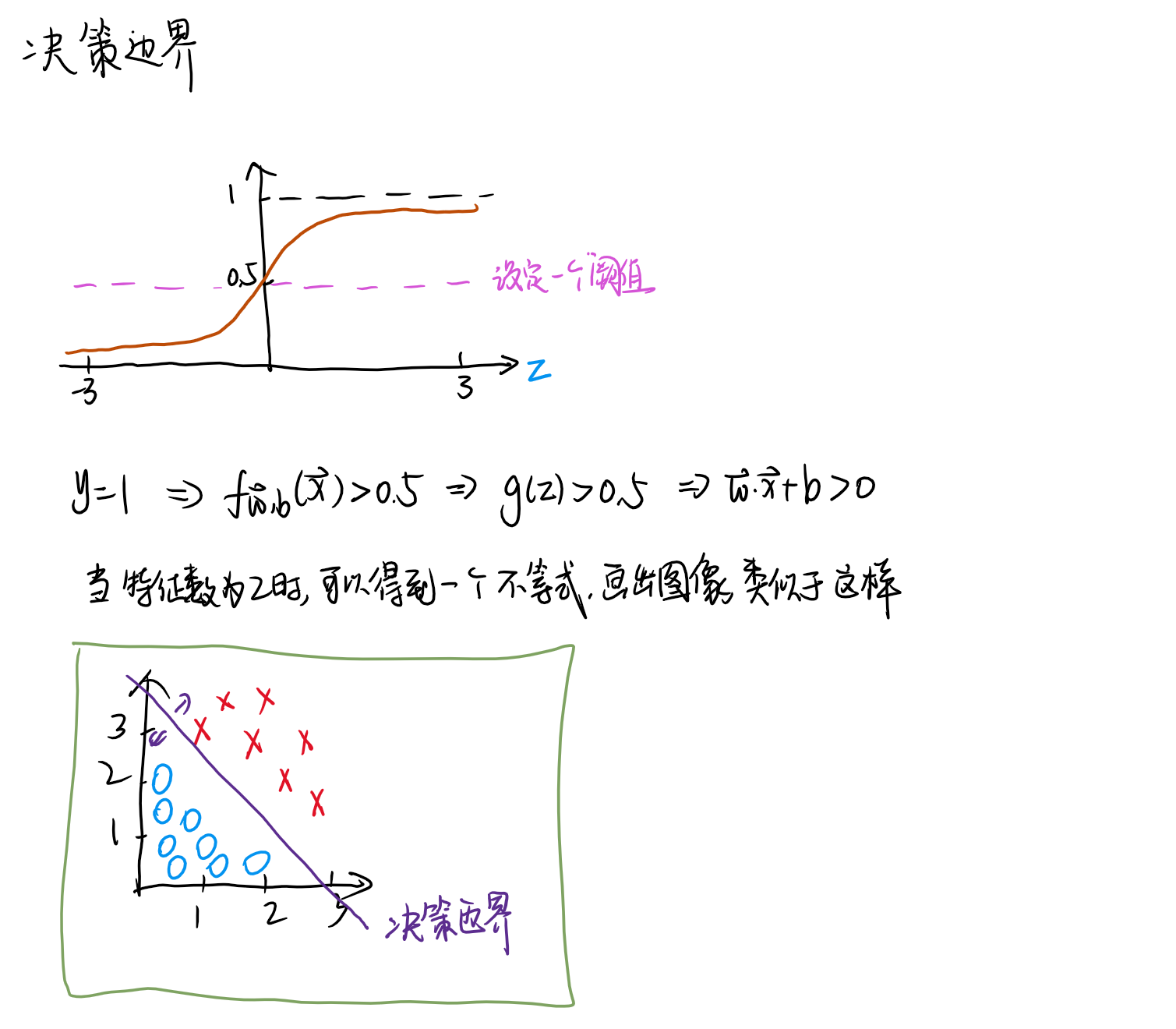
决策边界
确定一个阈值 → 列出表达式 → 找到决策边界函数
决策边界在线性的情况下是一条直接,当出现 x^2 这样的系数时,决策边界可以是任何可能的曲线形状
逻辑回归的损失函数
在线性回归中,我们使用梯度下降算法来找到最优参数。其中,损失函数使用的是平方误差成本函数,现这一函数应用在逻辑回归中不合适,因此我们使用了一种新的损失函数,使得能够通过梯度下降算法保证收敛到局部最小值。
- 平方误差成本函数已不适用于逻辑回归
- 使用 Loss 函数表示单个样本训练误差,Loss 函数得到的误差之和即为整体误差
- 逻辑回归成本函数使用新的带有 log 的逻辑函数
- 可以对这个新的成本函数进行一定的简化

逻辑回归的梯度下降算法
目标:确定 w 和 b。当有一个新的病例样本,其中提供了肿瘤的大小,就可以判断 y = 1的概率有多大了。
结论:和线性回归梯度下降差不多,区别的地方就是 f 函数变了一下

