梯度下降算法
梯度下降算法
梯度下降是一种算法，可以用来找到成本函数的局部最小值。这里用线性回归来演示梯度下降算法，但梯度下降不仅仅适用于线性回归成本函数。
梯度下降中，有学习率 α、数学表示等概念
梯度下降是什么
单变量线性回归梯度下降
梯度下降通过逐步更新参数，一步一步达到局部最小值
每一步的更新操作是这样的：
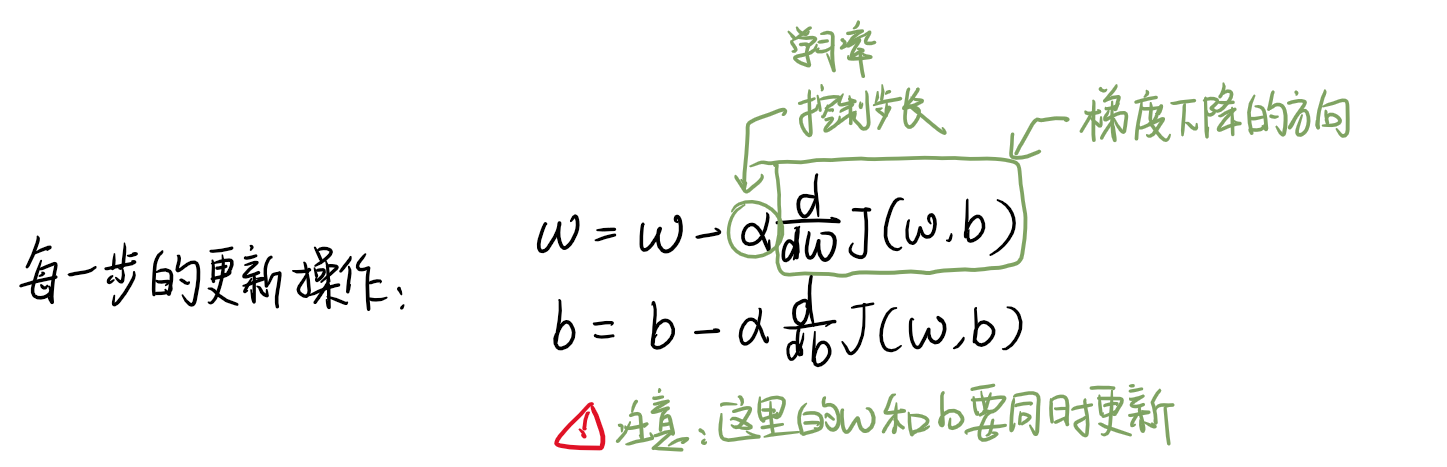
这里要注意 w 和 b 需要同时更新
进一步推导：
学习率 α
当学习曲线观察出异常时，可以将学习率调整为特别小的值，如果梯度仍未下降，可能是程序出现了bug；如果学习率调小后梯度正常，那可能是因为之前的学习率太大了。
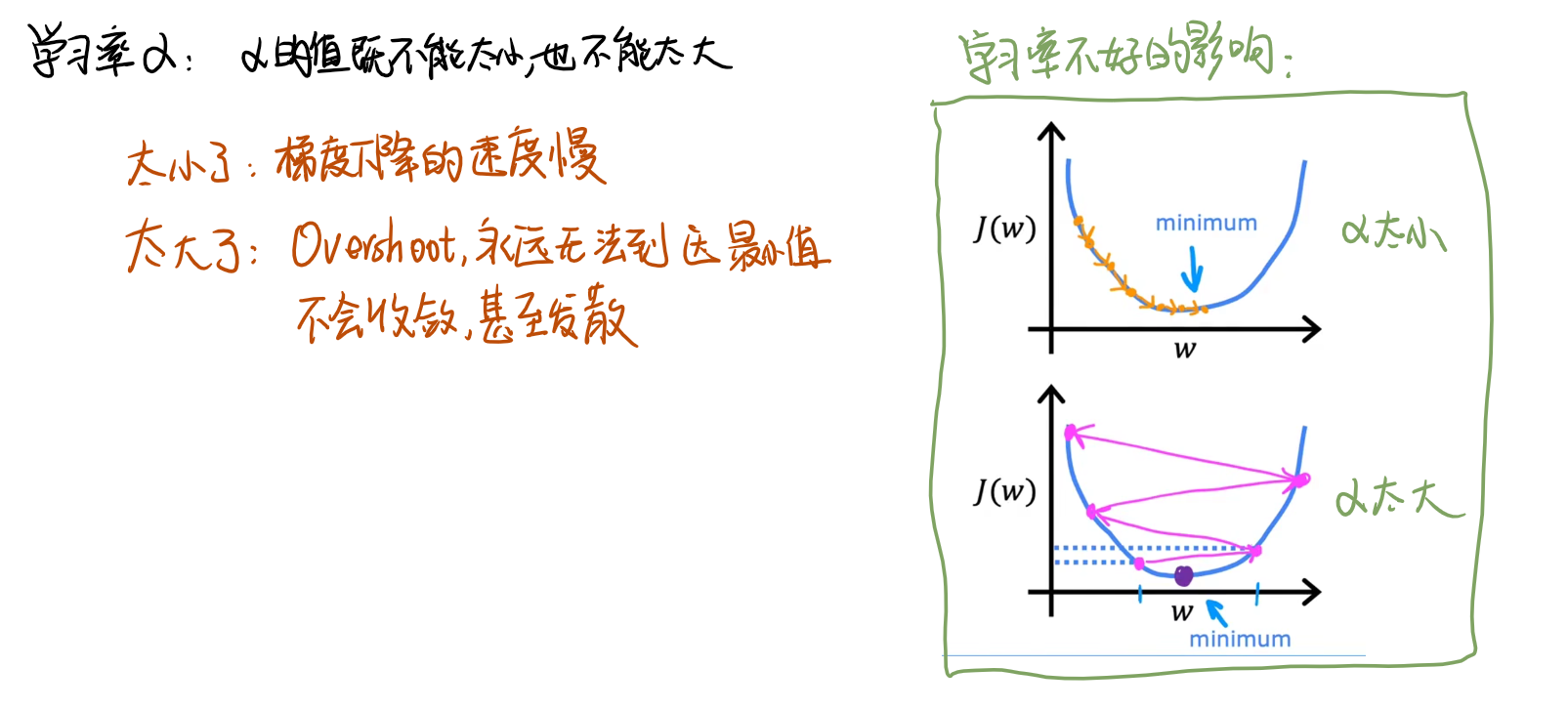
逐步达到最小值的趋势变化
多元线性回归梯度下降
多元线性回归就是有多个特征输入，变化的地方就是
- 输入的是特征向量 ω，而不是单一特征
- 计算的是 ωj，所以会计算 n 次 ωj
逻辑回归梯度下降
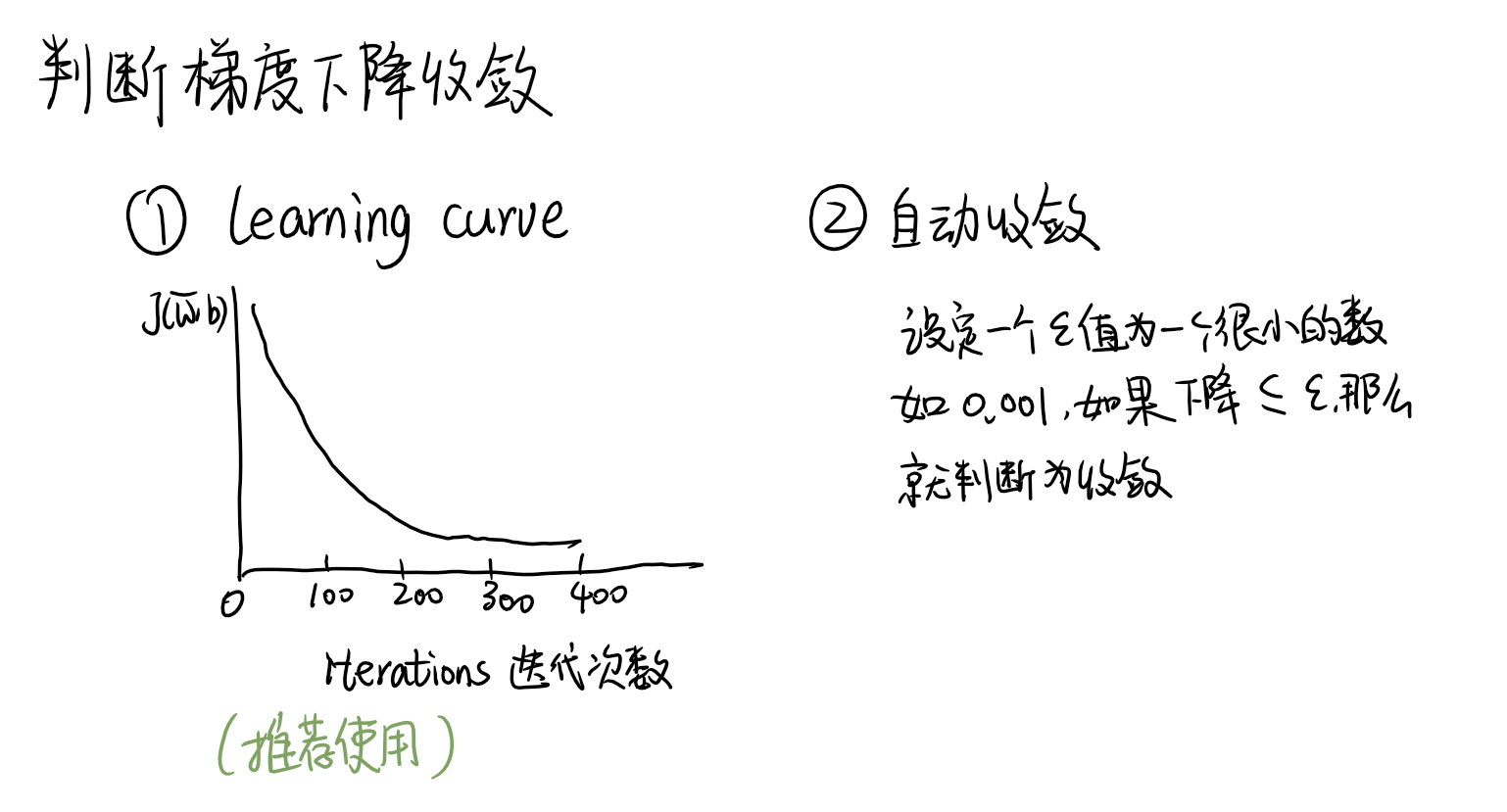
判断梯度下降是否开始收敛
两种方法：① 通过学习曲线观察 ② 使用自动收敛
梯度下降可选的优化
特征工程：选择合适的特征向量作为输入
多项式回归：不仅仅是使用线性函数，转而使用多项式、开根号等表达式表示回归函数。
