几种排序算法

题目链接

912. 排序数组

1. 快速排序

思路

快速排序的思想是分治

解题思路

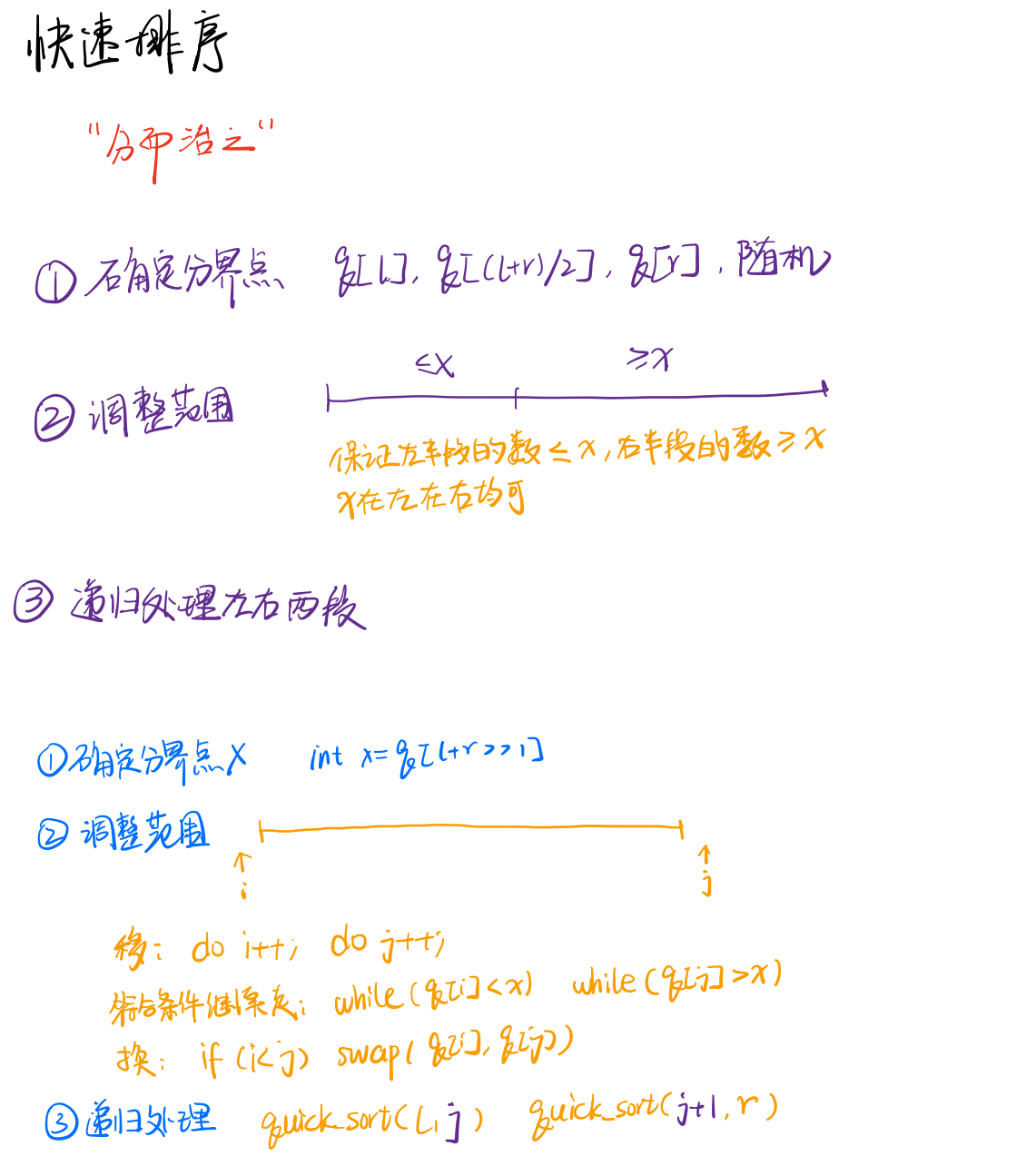
1. 确定分界点x，这里直接考虑 l + r >> 1
2. 调整范围，让左半段的数小于等于x，右半段的数大于等于x
3. 递归处理左右两段

这里分界点 x 只考虑 l + r >> 1，递归的边界是 j 和 j + 1。

和归并不同的是，快排是先调整范围，再递归的，而归并排序先递归。

i 和 j 先是初始化为 l - 1 和 r + 1

题解代码

void quick_sort(int l, int r) {
    
    if (l >= r) return;
    
    // 确定分界点
    int x = q[l + r >> 1], i = l - 1, j = r + 1;
    
    // 调整区间
    while (i < j) {
        do i++; while (q[i] < x);
        do j--; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    
    // 递归处理
    quick_sort(l, j), quick_sort(j + 1, r);
    
}

2. 归并排序

思路

算法的思想是分治

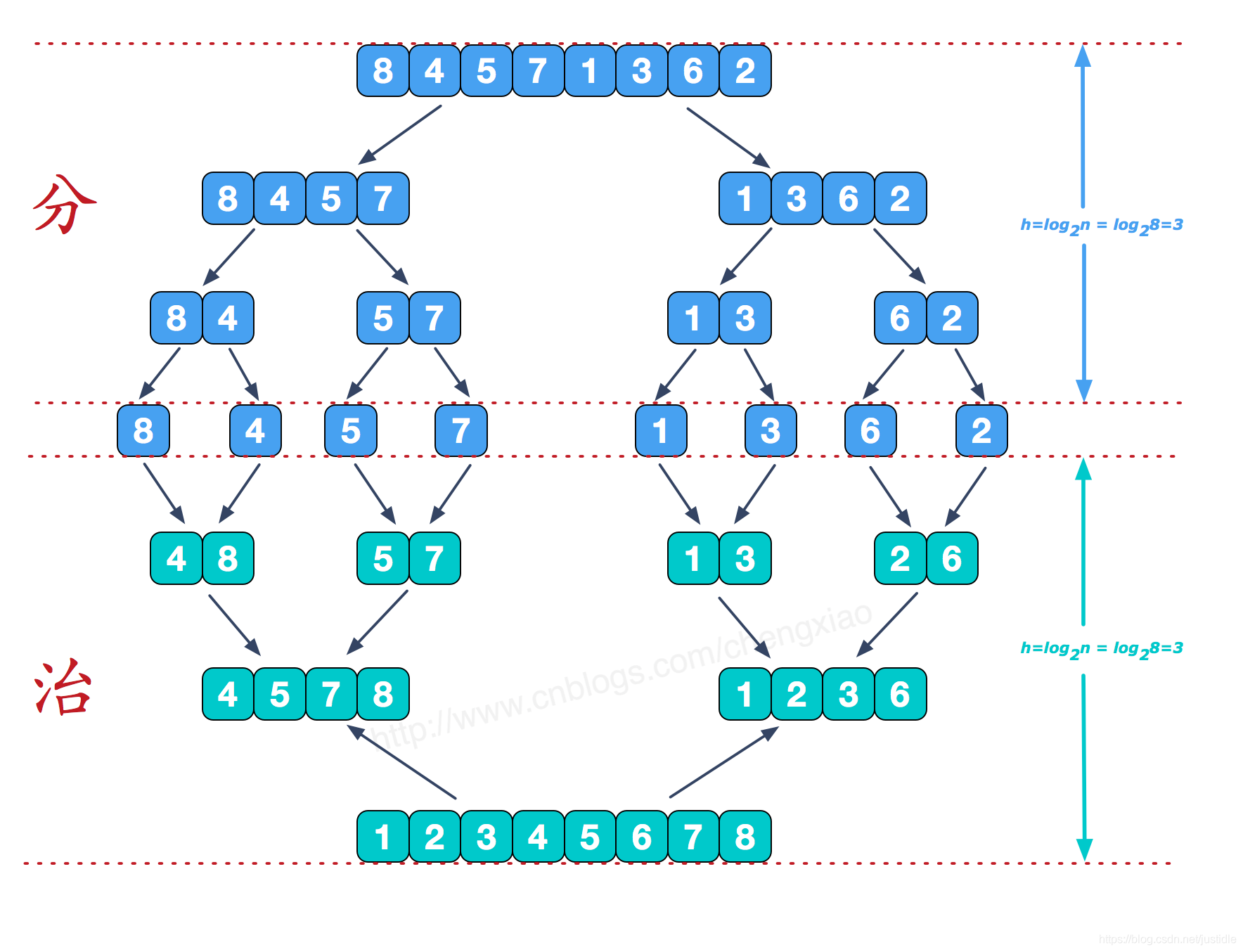
一句话总结：将排序的任务先递归分解成一个一个小的任务，将小的任务完成，再用小任务完成大任务，逐步完成最终得到整个排序的任务。

一张图片直观表示分治的思路：

题解思路

1. 上图中的每一层如何实现？

   通过递归的方式。将数组递归处理，处理 q[l, mid] 和 q[mid+1, r] 来实现

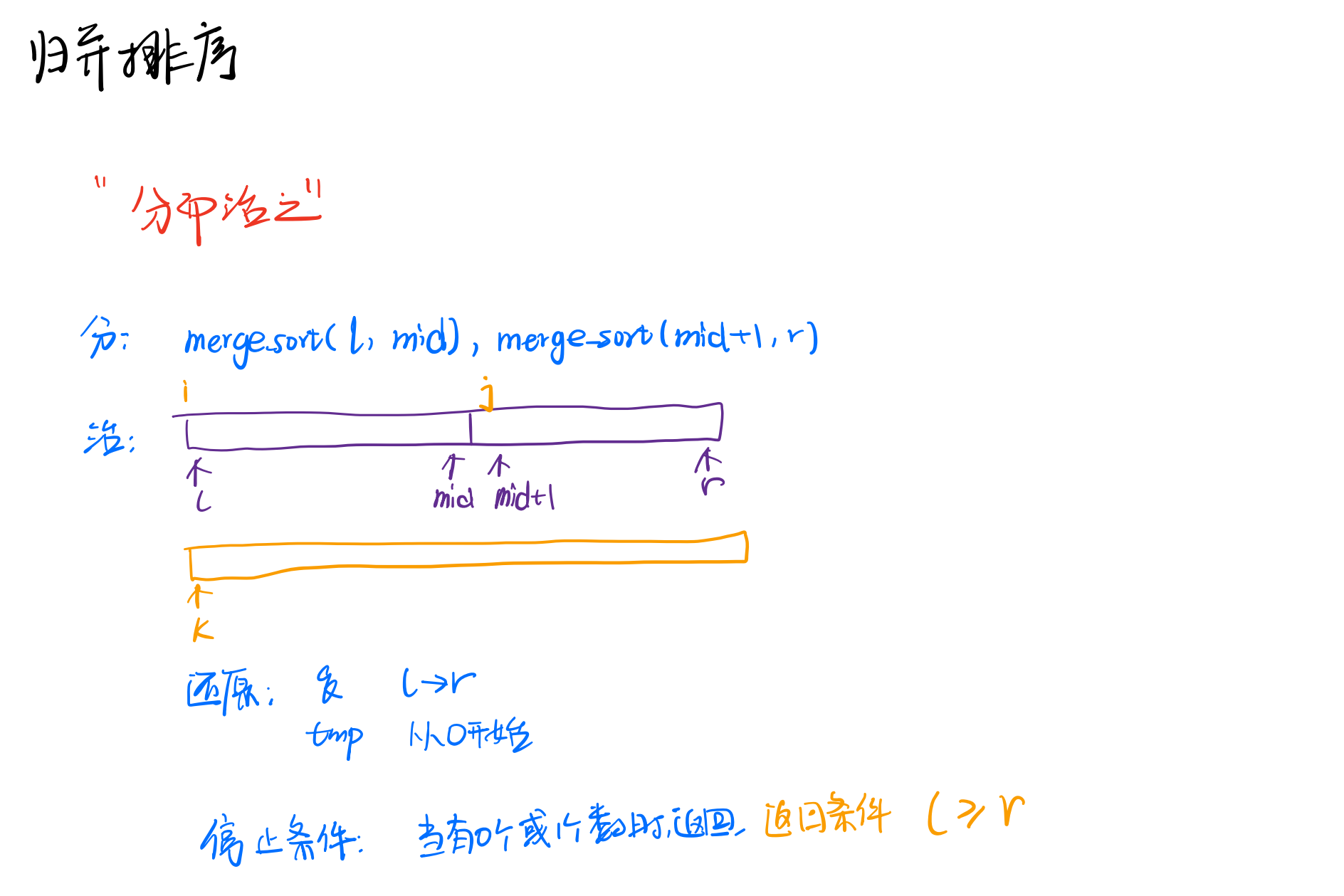
2. “治”中，如何实现两个子数组的有序合并？

   【两个有序数组的合并】问题可以通过双指针算法求解

题解模板

1. 通过函数调用递归来实现，因此参数传入为 int q[], int l, int r
2. 【递归结束条件】当小任务中有 0 个或者 1 个数时，返回
3. 【分】递归左边和右边
4. 【治】两个有序数组的合并
   • 设置辅助数组 tmp
   • 界定退出循环为：两个子数组有一个遍历完成
   • 将未遍历完的数据追加到尾部
   • 将 tmp 数组内容放回 q 中

题解代码

void merge_sort(int q[], int l, int r) {
    if (l >= r) return;
    
    // 分
    int mid = l + r >> 1;
    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
    
    // 治
    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r) {
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    }
    
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];
    
    for (int i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
    
}