二分搜索
整数二分模板(直接用)
思路

代码
int lower_bound(int target) {
int l = -1, r = n;
while (l + 1 < r) {
int mid = l + r >> 1;
if (q[mid] < target) {
l = mid;
} else {
r = mid;
}
}
return r;
}
题目
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
题目解读
在一个排序的数组中查找值。输出结果为:找到的话输出值开始位置和结束位置,找不到返回[-1,-1]。
题解方法
采用二分的方式。
题解视频
题解思路
- 先解决:返回有序数组中第一个
>= 8的数

- 过程解读
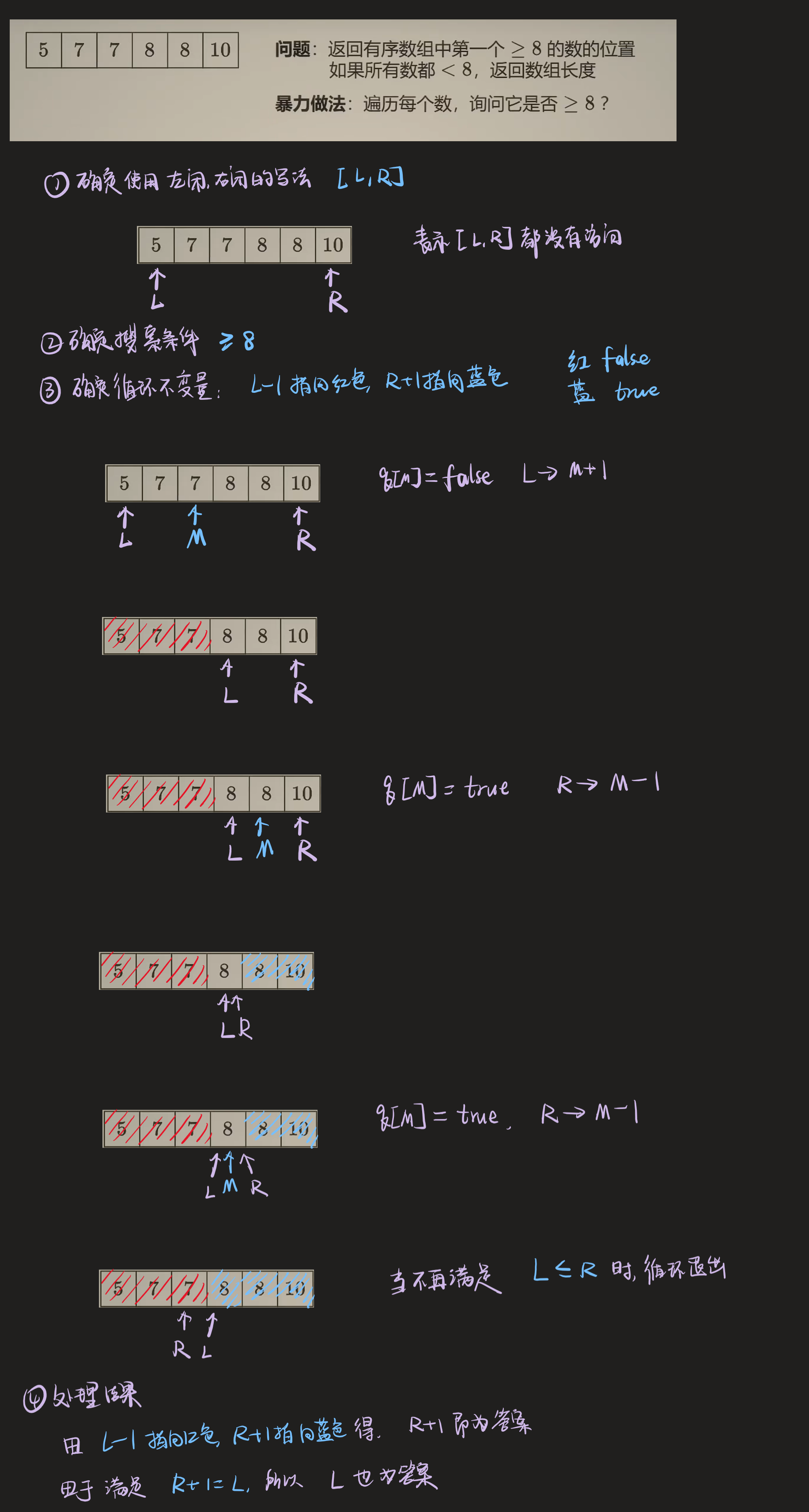
- 答题模板

- 判断条件的相互转换

题解模板
- 了解题目要求的是哪种类型,
>= xor> xor< xor<= x - 一律按照
>= x的情况处理。 - 采用两边开区间的方式,初始化 left = -1, right = n
- 判断退出条件:根据应当在
left + 1 == right的情况时结束循环,while中应填入 left + 1 < right。 - if 的条件:
if < x, left = mid; else right = mid; - 结果:因为要求的是满足
>= x的第一个值,应该是蓝色部分的第一个值,也就是right
题解代码
int lower_bound(vector<int>& nums, int target) {
int left = -1;
int right = nums.size();
while (left + 1 < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid;
} else {
right = mid;
}
}
return right;
}
其它情况
解的判定
- target 大于数组中所有的数
返回的结果为数组的长度 n
- target 小于数组中的所有的数
返回的值为 0,此时 nums[start] != target
- target 中没有找的这个数,比如 [1, 3, 3, 6, 6, 8], target = 7
返回的值为 数字8 的下标,此时 nums[start] != target
题目的完整代码
int lower_bound(vector<int>& nums, int target) {
int left = -1;
int right = nums.size();
while (left + 1 < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid;
} else {
right = mid;
}
}
return right;
}
vector<int> searchRange(vector<int>& nums, int target) {
int start = lower_bound(nums, target);
if (start == nums.size() || nums[start] != target) {
return {-1, -1};
}
int end = lower_bound(nums, target + 1) - 1;
return {start, end};
}

