NOIP 模拟赛

　　　　　　NOIP 模拟赛

思路：求 n , m 的 gcd，然后用 n , m 分别除以 gcd；若 n 或 m 为偶数，则输出 1/2.

　　特别的，当 n = m = 1 时，应输出 1/1

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
typedef long long LL;
LL n, m;

LL gcd(LL x, LL y) {
    return y == 0 ? x : gcd(y, x % y);
}

int main() {
    freopen("line.in","r",stdin);
    freopen("line.out","w",stdout);
    cin >> n >> m;
    if (n == m && m == 1) return printf("1/1\n"), 0;
    LL tmp = gcd(n, m);
    n /= tmp; m /= tmp;
    if (!(n & 1) || !(m & 1)) return printf("1/2\n"), 0;
    
    fclose(stdin); fclose(stdout);
    return 0;
}

正解：题目要求的是比值，故当 m 与 n 不互质时，我们可以求出 m 和 n 的最大公约数 d，并将 m /= d, n /= d，并不影响结果。故我们现在假定 m 和 n 互质。若m 和 n 中有一个为偶数， 那么根据对称性， 答案就是 1/2。 如果 m 和 n 均为奇数，那么答案就是(n*m+1) / (2*m*n）。

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
typedef long long LL;
LL n, m, d;

LL gcd(LL x, LL y) {
    return x % y ? gcd(y, x % y) : y;
}

int main() {
    freopen("line.in","r",stdin);
    freopen("line.out","w",stdout);
    cin >> n >> m;
    d = gcd(n, m);
    n /= d, m /= d;
    if ((n + m) & 1) cout << "1/2" << endl;
    else cout << (n * m + 1) / 2 << "/" << n * m << endl;
    return 0;
}

 

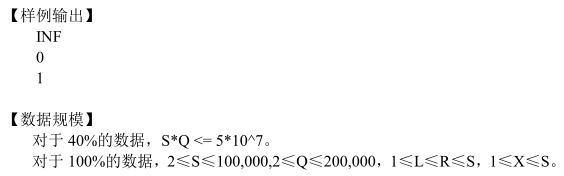
思路：线段树维护是否有浓雾。一开始都没有，建树时每个位置的值都赋为 1；若进行 1 或 2 操作，用 flag 标记，因为是区间直接赋值，所以两种操作只需要一个标记即可。查询写错了，导致100 -> 10，对题意理解稍有偏差。

#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 100005;
int n, m, k, x, y;
struct nond {
    int ll, rr;
    int sum;
    int flag;
} tree[N << 2];

inline void update(int now) {
    tree[now].sum = tree[now << 1].sum + tree[now << 1 | 1].sum;
}

inline void down(int now) {
    if (tree[now].flag == 1) {
        tree[now << 1].flag = 1;
        tree[now << 1 | 1].flag = 1;
        tree[now << 1].sum = tree[now << 1].rr - tree[now << 1].ll + 1;
        tree[now << 1 | 1].sum = tree[now << 1 | 1].rr - tree[now << 1 | 1].ll + 1;
    }
    else {
        tree[now << 1].flag = -1;
        tree[now << 1 | 1].flag = -1;
        tree[now << 1].sum = 0;
        tree[now << 1 | 1].sum = 0;
    }
    tree[now].flag = 0;
    return ;
}

inline void build(int now, int l, int r) {
    tree[now].ll = l; tree[now].rr = r;
    tree[now].flag = 0; tree[now].sum = 1;
    if (l == r) return ;
    int mid = (l + r) >> 1;
    build(now << 1, l, mid);
    build(now << 1 | 1, mid + 1, r);
    update(now);
}

inline void change(int now, int l, int r) {
    if (tree[now].ll == l && tree[now].rr == r) {
        tree[now].flag = -1;
        tree[now].sum = 0;
        return ;
    }
    if (tree[now].flag != 0) down(now);
    int mid = (tree[now].ll + tree[now].rr) >> 1;
    if (l <= mid && mid < r) change(now << 1, l, mid), change(now << 1 | 1, mid + 1, r);
    else if (r <= mid) change(now << 1, l, r);
    else change(now << 1 | 1, l, r);
    update(now);
}

inline void become(int now, int l, int r) {
    if (tree[now].ll == l && tree[now].rr == r) {
        tree[now].flag = 1;
        tree[now].sum = tree[now].rr - tree[now].ll + 1;
        return ;
    }
    if (tree[now].flag != 0) down(now);
    int mid = (tree[now].ll + tree[now].rr) >> 1;
    if (l <= mid && mid < r) become(now << 1, l, mid), become(now << 1 | 1, mid + 1, r);
    else if (r <= mid) become(now << 1, l, r);
    else become(now << 1 | 1, l, r);
    update(now);
}

inline int query(int now, int l, int r) {
    if (tree[now].ll == l && tree[now].rr == r)
        return tree[now].sum;
    if (tree[now].flag != 0) down(now);
    int mid = (tree[now].ll + tree[now].rr) >> 1;
    if (l <= mid && mid < r) return query(now << 1, l, mid) + query(now << 1 | 1, mid + 1, r);
    else if (r <= mid) return query(now << 1, l, r);
    else return query(now << 1 | 1, l, r);
}

int main() {
    freopen("explore.in","r",stdin);
    freopen("explore.out","w",stdout);
    scanf("%d%d", &n, &m);
    build(1, 1, n);
    for (int i = 1; i <= m; ++i) {
        scanf("%d%d", &k, &x);
        if (k == 1) { scanf("%d", &y); change(1, x, y); }
        else if (k == 2) { scanf("%d", &y); become(1, x, y); }
        else {
            if (query(1, x, x) == 0) printf("0\n");
            else {
                if (query(1, 1, x) == x || query(1, x, n) == n - x + 1)
                    printf("INF\n");
                else for (int j = 1; j <= (n >> 1); ++j) {
                    int tmp = query(1, x - j, x + j);
                    if (tmp != j << 1 | 1) { printf("%d\n", tmp); break; }
                }
            }
        }
    }
    fclose(stdin); fclose(stdout);
    return 0;
}

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#define fortodo(i, f, t) for (i = f; i <= t; i++)
using namespace std;

int lsd[200001], rsd[200001], lsid[200001], rsid[200001], cov[200001], segsize;
bool emp[200001];

int SEG_Build(int L, int R) {
    int Nid = ++segsize;
    lsd[Nid] = L;
    rsd[Nid] = R;
    emp[Nid] = true;
    cov[Nid] = 0;
    if (L == R) lsid[Nid] = rsid[Nid] = -1;
    else {
        lsid[Nid] = SEG_Build(L, (L + R) / 2);
        rsid[Nid] = SEG_Build((L + R) / 2 + 1, R);
    };
    return Nid;
};

bool SEG_Empty(int Nid) {
    if (cov[Nid] == 0) return true;
    if (cov[Nid] == 1) return false;
    return emp[Nid];
};

void SEG_Reemp(int Nid) {
    emp[Nid] = SEG_Empty(lsid[Nid]) && SEG_Empty(rsid[Nid]);
};

void SEG_Inherit(int Nid) {
    if (cov[Nid] == -1) return;
    if (lsd[Nid] == rsd[Nid]) return;
    cov[lsid[Nid]] = cov[Nid];
    cov[rsid[Nid]] = cov[Nid];
    cov[Nid] = -1;
    SEG_Reemp(Nid);
};

void SEG_Paint(int Nid, int L, int R, int Color) {
    SEG_Inherit(Nid);
    if ((L == lsd[Nid]) && (R == rsd[Nid])) {
        cov[Nid] = Color;
        return;
    };
    int Div = (lsd[Nid] + rsd[Nid]) / 2;
    if (L >  Div) SEG_Paint(rsid[Nid], L, R, Color);
    if (R <= Div) SEG_Paint(lsid[Nid], L, R, Color);
    if ((L <= Div) && (R > Div)) {
        SEG_Paint(lsid[Nid], L, Div, Color);
        SEG_Paint(rsid[Nid], Div + 1, R, Color);
    };
    SEG_Reemp(Nid);
};

bool SEG_Query(int Nid, int L, int R) {
    SEG_Inherit(Nid);
    if (SEG_Empty(Nid)) return true;
    if ((L == lsd[Nid]) && (R == rsd[Nid])) return SEG_Empty(Nid);
    int Div = (lsd[Nid] + rsd[Nid]) / 2;
    if (L >  Div) return SEG_Query(rsid[Nid], L, R);
    if (R <= Div) return SEG_Query(lsid[Nid], L, R);
    return SEG_Query(lsid[Nid], L, Div) && SEG_Query(rsid[Nid], Div + 1, R);
};

int S, Q;
int i, j;
int Opt, X, Y;

void Answer(int P) {
    if (!SEG_Query(1, P, P)) {
        printf("0\n");
        return;
    };
    if ((SEG_Query(1, 1, P)) || (SEG_Query(1, P, S))) {
        printf("INF\n");
        return;
    };
    int L, R, M, Ans[2];
    L = 2; R = P;
    while (L < R) {
        M = (L + R) / 2;
        if (SEG_Query(1, M, P)) R = M;
        else L = M + 1;
    };
    Ans[0] = L;
    L = P; R = S - 1;
    while (L < R) {
        M = (L + R + 1) / 2;
        if (SEG_Query(1, P, M))
            L = M;
        else
            R = M - 1;
    };
    Ans[1] = L;
    printf("%d\n", Ans[1] - Ans[0] + 1);
};

int main() {
    freopen("explore.in", "r", stdin);
    freopen("explore.out", "w", stdout);
    scanf("%d%d", &S, &Q);
    segsize = 0;
    SEG_Build(1, S);
    fortodo(i, 1, Q) {
        scanf("%d%d", &Opt, &X);
        if (Opt != 3) scanf("%d", &Y);
        if (Opt == 1) SEG_Paint(1, X, Y, 1);
        if (Opt == 2) SEG_Paint(1, X, Y, 0);
        if (Opt == 3) Answer(X);
    };
    return 0;
};

 

思路：

　　1.暴搜  写挂了，样例都过不了

　　2.树形DP  不会写 后来讲题时发现自己想法是错的

　　3.并查集  将直接连接两个有苹果的节点的边打上标记，记录边权和，但仍会存在多个苹果间接相连的情况，没有想到解决办法

然后我就交了唯一一个过了样例但是最不靠谱的 3 

然后就暴零了 T^T。。。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int M = 100005;
int n, m, tot;
int t[M], fc[M];
int fa[M], f[M];
struct nond {
    int u, v, w;
    int flag;
}e[M];

int find(int x) {
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

bool flag = false;
inline void dfs(int now) {  //可以明显看到没写完 因为不会写了 qwq
    if (f[now] == 1) flag = 1;
    
}

long long ans;
int main() {
    freopen("apple.in","r",stdin);
    freopen("apple.out","w",stdout);
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; ++i) fa[i] = i;
    for (int i = 1; i < n; ++i) {
        scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);
        e[i].flag = 0;
    }
    for (int i = 1; i <= m; ++i) {
        scanf("%d", &t[i]);
        f[t[i]] = 1;
    }
    for (int i = 1; i < n; ++i) {
        if (f[e[i].u] == 1 && f[e[i].v] == 1) {
            e[i].flag = 1;
            ans += e[i].w;
            ++tot;
            continue;
        }
        int x = find(e[i].u), y = find(e[i].v);
        fa[x] = y;
        
    }
    if (tot == m - 1) cout << ans;
    else {
        for (int i = 0; i < n; ++i)
            ++fc[find(i)];
        for (int i = 0; i < n; ++i) {
            if (fc[i] > 1) dfs(i);
            if (tot == m - 1) break;
        }
        cout << ans;
    }
    fclose(stdin); fclose(stdout);
    return 0;
}

正解：

　　

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <string>
#include <cstdio>
#include <cmath>
#define REP(i, n) for (int i = 0; i < (n); ++i)
#define FOR(i, a, b) for (int i = (a); i <= (b); ++i)
#define ROF(i, a, b) for (int i = (a); i >= (b); --i)
#define FEC(p, u) for (edge *p = G.head[u]; p; p = p->nxt)
using namespace std;
typedef long long LL;
LL inf = 1LL<<60;

int n, rt;
bool a[200000];
LL f[200000], g[200000];

struct edge {
    int b, len;
    edge *nxt;
} e[300000], *le;
struct graph {
    edge *head[200000];
    void init() {
        le = e;
        REP(i, n) head[i] = NULL;
    }
    void add(int x, int y, int z) {
        le->b = y, le->len = z, le->nxt = head[x], head[x] = le++;
    }
} G;

int fa[200000];
LL pre[200000];
int q[200000];
void init() {
    int k, u, v, w;
    scanf("%d%d", &n, &k);
    G.init();
    REP(i, n-1) {
        scanf("%d%d%d", &u, &v, &w);
        G.add(u, v, w);
        G.add(v, u, w);
    }
    while (k--) {
        scanf("%d", &u);
        a[u] = true;
    }
    rt = u;
}

void bfs() {
    int R = 0;
    q[0] = rt;
    REP(L, n)
    FEC(p, q[L]) if (p->b != fa[q[L]]) {
        fa[p->b] = q[L];
        pre[p->b] = p->len;
        q[++R] = p->b;
    }
}

void work() {
    ROF(i, n - 1, 0) {
        int x = q[i];
        if (a[x]) {
            FEC(p, x) if (p->b != fa[x]) g[x] += f[p->b];
            f[x] = g[x]+pre[x];
        }
        else {
            FEC(p, x) if (p->b != fa[x])    f[x] += f[p->b];
            g[x] = inf;
            FEC(p, x) if (p->b != fa[x]) g[x] = min(g[x], f[x] - f[p->b] + g[p->b]);
            f[x] = min(f[x], g[x]+pre[x]);
        }
    }
}

int main() {
    freopen("apple.in", "r", stdin);
    freopen("apple.out", "w", stdout);
    init();
    bfs();
    work();
    cout << f[rt] << endl;
    return 0;
}