18/9/22NOIP模拟考
18/9/22NOIP模拟考


其实本来是有多组数据的,出题人忘记在题面上加了 斜眼笑
期望得分:100;实际得分:100
由于种种原因,拿到题的时候已经过去了0.5h+。。。
然后因为这道题数据范围比较大,所以。。就想到了找规律
没想到居然A了 开心
这道题一共出现了三种做法:
1.出题人的std:据说是旋转坐标系什么鬼的,没听说过。。。
2.某人:从一个点做一个斜率为±1的一次函数,然后。。。如图
3.大部分人(包括我):分别求出两点横纵坐标之差的绝对值,然后取max,完事
4.极少部分人:模拟 or 暴力?

#include <algorithm> #include <iostream> #include <cstring> #include <cstdlib> #include <cstdio> using namespace std; typedef long long LL; LL n, s, t, c, f; int main() { freopen("grid.in","r",stdin); freopen("grid.out","w",stdout); scanf("%I64d%I64d%I64d%I64d%I64d", &n, &s, &t, &c, &f); LL a = abs(s - c), b = abs(t - f); cout << max(a, b) << '\n'; fclose(stdin); fclose(stdout); return 0; }

#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cctype> #include<cmath> #include<set> #include<map> #include<queue> #include<vector> #include<cassert> using namespace std; typedef long long LL; inline int read() { int x = 0, f = 1; char ch = getchar(); for (; !isdigit(ch); ch=getchar()) if (ch=='-') f = -1; for (; isdigit(ch); ch=getchar()) x = x * 10 + ch - '0'; return x * f; } LL dx[4] = {0, 0, 1, -1}; LL dy[4] = {1, -1, 0, 0}; LL getdis(LL a,LL b,LL c,LL d,int flag) { if (flag) { // black a = (a - 1) / 2, b = (b - 1) / 2, c = (c - 1) / 2, d = (d - 1) / 2; return abs(a - c) + abs(b - d); } else { // white a /= 2, b /= 2, c /= 2, d /= 2; return abs(a - c) + abs(b - d); } } void getxy(LL a,LL b,LL &t1,LL &t2) { t1 = a + b,t2 = b - a; } int main() { freopen("grid.in","r",stdin); freopen("grid.out","w",stdout); LL Case,n, a, b, c, d, t1, t2, t3, t4, t5, t6; // cin >> Case; // while (Case--) { cin >> n >> a >> b >> c >> d; assert(a <= n); assert(b <= n); assert(c <= n); assert(d <= n); t1 = a + b, t2 = b - a; t3 = c + d, t4 = d - c; int f1, f2; if ((t1 & 1) && (t2 & 1)) f1 = 1; else f1 = 0; if ((t3 & 1) && (t4 & 1)) f2 = 1; else f2 = 0; LL ans = 1e18; if (f1 == f2) ans = getdis(t1, t2, t3, t4, f1); else { for (int i=0; i<4; ++i) { LL x = a + dx[i], y = b + dy[i]; if (x >= 1 && x <=n && y >= 1 && y <= n) { getxy(x, y, t5, t6); ans = min(ans, getdis(t3, t4, t5, t6, f2) + 1); } } for (int i=0; i<4; ++i) { LL x = c + dx[i], y = d + dy[i]; if (x >= 1 && x <=n && y >= 1 && y <= n) { getxy(x, y, t5, t6); ans = min(ans, getdis(t1, t2, t5, t6, f1) + 1); } } } cout << ans << "\n"; // } return 0; }






期望得分:0;实际得分:0
其实还是希望有些分的,然而暴力没有调出来。。。
然后就gg了 qwq
正解:如果写了dfs的话,可以看出:我们只要知道上次填的串多长,就可以知道上次使用的字符串。而且对每个位置只需要知道它上次填2或3时是否可行。
$f[i][2/3]$表示当前到$i$,以$i$开头,长度为2/3的的后缀串是否可行。可以转移就记录答案。
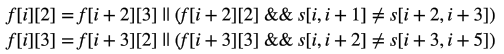
如果type ≠ 0,则不需要判断后缀是否相同
为了方便,可以把串反过来
复杂度:O(n)

#include <cstdio> #include <cstring> #include <algorithm> #define pc putchar const int N=50005; bool f[N][2]/*0:2 1:3*/,ok2[28][28],ok3[28][28][28]; char s[N]; void Work(const int type) { memset(f,0,sizeof f); memset(ok2,0,sizeof ok2), memset(ok3,0,sizeof ok3); scanf("%s",s+1); int n=strlen(s+1); std::reverse(s+1,s+1+n); int tot=0; n-=3; if(n>=2) f[2][0]=1, ++tot, ok2[s[2]-'a'][s[1]-'a']=1; if(n>=3) f[3][1]=1, ++tot, ok3[s[3]-'a'][s[2]-'a'][s[1]-'a']=1; for(int i=4; i<=n; ++i) { int a=s[i]-'a', b=s[i-1]-'a', c=s[i-2]-'a'; if(f[i-2][1]||(f[i-2][0]&&(type||s[i]!=s[i-2]||s[i-1]!=s[i-3]))) { f[i][0]=1; if(!ok2[a][b]) ++tot, ok2[a][b]=1; } if(f[i-3][0]||(f[i-3][1]&&(type||s[i]!=s[i-3]||s[i-1]!=s[i-4]||s[i-2]!=s[i-5])))//i>=6 { f[i][1]=1; if(!ok3[a][b][c]) ++tot, ok3[a][b][c]=1; } } printf("%d\n",tot); for(int i=0; i<27&&tot; ++i) { for(int j=0; j<27; ++j) { if(ok2[i][j]) --tot,pc(i+'a'),pc(j+'a'),pc('\n'); for(int k=0; k<27; ++k) if(ok3[i][j][k]) --tot,pc(i+'a'),pc(j+'a'),pc(k+'a'),pc('\n'); } } } int main() { freopen("ling.in","r",stdin); freopen("ling.out","w",stdout); int T,type; for(scanf("%d%d",&T,&type); T--; Work(type)); return 0; }




一看要求期望。。。一脸不可做。。。
整场考试也就瞄了几眼,一点想做的念头都没有。。。
蒻的一批。。。
事实证明,真心难啊 qwq





#include <cstdio> #include <cctype> #include <assert.h> #include <algorithm> #define gc() getchar() const int N=5e5+5; int n,sz[N],fa[N],q[N],H[N],Enum,to[N],nxt[N]; double pw[N];//2^{-i} inline int read() { int now=0;register char c=gc(); for(;!isdigit(c);c=gc()); for(;isdigit(c);now=now*10+c-'0',c=gc()); return now; } inline void AddEdge(int u,int v) { fa[v]=u, ++sz[u], ++sz[fa[u]]; to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum; } double Calc(int x) { if(!sz[x]) return 0;//sz:子树内点数 int t=0;//t:子节点数 for(int i=H[x]; i; i=nxt[i]) q[t++]=to[i]; if(t==sz[x])//D=2 return 1-pw[t]; else { double ans=0; for(int s=1; s<1<<t; ++s) { int tot=0; for(int i=0; i<t; ++i) if(s>>i&1) for(int j=H[q[i]]; j; j=nxt[j]) assert(!H[to[j]]), ++tot; ans+=pw[t]*(pw[tot]*1+(1-pw[tot])*2); } return ans; } } void Subtask3(int Q) { static int dep[N]; int H=0; dep[1]=0; while(Q--) { int opt=read(),x=read(); if(opt==1) dep[++n]=++H; else { int h=H-dep[x]; double ans=h*pw[h]; for(int i=1; i<h; ++i) ans+=i*pw[i+1]; printf("%.10lf\n",ans); } } } int main() { freopen("threebody.in","r",stdin); freopen("threebody.out","w",stdout); n=1; int T=read(), Q=read(); pw[0]=1; for(int i=1; i<=Q; ++i) pw[i]=pw[i-1]*0.5; if(T==4) {Subtask3(Q); return 0;} while(Q--) { int opt=read(),x=read(); if(opt==1) AddEdge(x,++n); else if(T==3) printf("%.10lf\n",1-pw[sz[x]]);//Subtask2 else printf("%.10lf\n",Calc(x));//Subtask1 } return 0; }

#include <cstdio> #include <cctype> #include <assert.h> #include <algorithm> #define gc() getchar() #define MAX_H 60 const int N=5e5+5; int n,fa[N]; double f[N][MAX_H]; inline int read() { int now=0;register char c=gc(); for(;!isdigit(c);c=gc()); for(;isdigit(c);now=now*10+c-'0',c=gc()); return now; } int main() { freopen("threebody.in","r",stdin); freopen("threebody.out","w",stdout); n=1; for(int i=0; i<MAX_H; ++i) f[1][i]=1; for(int T=read(), Q=read(); Q--; ) { int opt=read(),x=read(); if(opt==1) { fa[++n]=x; for(int i=0; i<MAX_H; ++i) f[n][i]=1; double tmp1=f[x][0],tmp2; f[x][0]*=0.5; for(int Fa=fa[x],i=1; Fa&&i<MAX_H; Fa=fa[x=Fa],++i) { tmp2=f[Fa][i]; f[Fa][i] /= 0.5 + 0.5*tmp1; f[Fa][i] *= 0.5 + 0.5*f[x][i-1]; tmp1=tmp2; } } else { double ans=0; assert(x<=n); for(int i=1; i<MAX_H; ++i) ans+=(f[x][i]-f[x][i-1])*i; printf("%.10lf\n",ans); } } return 0; }





