18/9/16牛客网提高组Day2

　　　　　　牛客网提高组Day2

T1 方差

　　第一眼看就知道要打暴力啊，然而并没有想到去化简式子。。。

　　可能因为昨晚没睡好，今天上午困死

　　导致暴力打了一个半小时，还不对。。。

#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cmath>
using namespace std;
typedef long long LL;
const int M = 100005;
int n, m;
double sum;
LL a[M], s[M], f[M];

double mul(double a, int b) {
    double res = 0.0;
    while (b) {
        if (b & 1) res += a;
        a += a;
        b >>= 1;
    }
    return 0;
}

int main() {
    scanf("%d", &n);
    m = n - 1;
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        sum += a[i];
    }
    for (int i = 1; i <= n; i++) {
        if (f[a[i]] != 0) {
            if(i != n) printf("%lld ", f[a[i]]);
            else return printf("%lld\n", f[a[i]]), 0;
            continue;
        }
        double tmp = 1.0 * (sum - a[i]) / m;
        double ss;
        for (int j = 1; j <= n; j++) {
            if (i == j) continue;
            double t = abs(a[j] - tmp);
            t = 1.0 * t * t;
            ss += t;
        }
        f[a[i]] = mul(ss, m);
        if(i != n) printf("%lld ", f[a[i]]);
        else printf("%lld\n", f[a[i]]);
    }
    return 0;
}

正解：

　　题中公式可进行化简，转化为只需维护序列元素的和，平方和即可

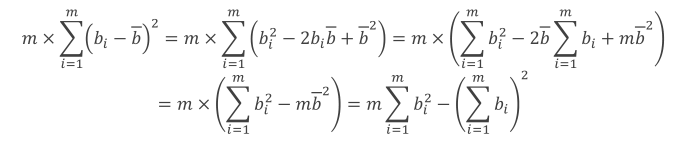
#include<iostream>
#include<cstdio>
using namespace std;
const int M = 100002;
int n;
long long s, s2, ans;
long long a[M];

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%lld", &a[i]);
        s += a[i];
        s2 += a[i] * a[i];
    }
    for (int i = 1; i <= n; i++) {
        ans = (n - 1) * (s2 - a[i] * a[i]) - (s - a[i]) * (s - a[i]);
        printf("%lld ", ans);
    }
    return 0;
}

T2 分糖果

　　暴力搜索 然而并没有分 qwq。。。

#include <algorithm>
#include <iostream>
#include <cstdio>
using namespace std;
const int M = 110;
int n, ans;
int f[M], a[M], vis[M];

void dfs(int step) {
    if(step == n + 1) ans++;
    else for(int j = 1; j <= f[step]; j++) {
        if(!vis[j] && step == n && (a[step - 1] != j) && a[1] != j) {
            a[step] = j;
            dfs(step + 1);
        }
        else if(!vis[j] && (a[step - 1] != j) && step != n) {
            a[step] = j;
            dfs(step + 1);
        }
    }

}

int main() {
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
        scanf("%d", &f[i]);
    dfs(1);
    printf("%d\n", ans);
    return 0;
}

正解：

　　

暴力复杂度为O(n^2)，所以考虑优化：

　　线段树优化：O(nlogn) 80pts

　　单调队列优化：O(n) 100pts

#include<bits/stdc++.h>
using namespace std;
const int M = 1000005;
const int P = 1e9 + 7;
int n, B[M], A[M];
int dp[M], sum[2];
int q[2][M], val[2][M], l[2], r[2];

void insert(int f, int x, int s) {
    while (l[f] < r[f] && q[f][r[f] - 1] >= x) {
        r[f]--;
        s = (s + val[f][r[f]]) % P;
        sum[f] = (sum[f] - 1ll * val[f][r[f]] * q[f][r[f]] % P + P) % P;
    }
    val[f][r[f]] = s;
    q[f][r[f]++] = x;
    sum[f] = (sum[f] + 1ll * s * x % P) % P;
    s = 0;
    while (l[1 - f] < r[1 - f] && q[1 - f][r[1 - f] - 1] >= x) {
        r[1 - f]--;
        s = (s + val[1 - f][r[1 - f]]) % P;
        sum[1 - f] = (sum[1 - f] - 1ll * val[1 - f][r[1 - f]] * q[1 - f][r[1 - f]] % P + P) % P;
    }
    if (s) {
        val[1 - f][r[1 - f]] = s;
        q[1 - f][r[1 - f]++] = x;
        sum[1 - f] = (sum[1 - f] + 1ll * s * x % P) % P;
    }
}

int main() {
    scanf("%d", &n);
    int mi = 1, ans = 0;
    for (int i = 1; i <= n; i++) {
        scanf("%d", &B[i]);
        if (B[mi] > B[i])mi = i;
    }
    int len = 0;
    for (int i = mi; i <= n; i++) A[++len] = B[i];
    for (int i = 1; i < mi; i++) A[++len] = B[i];
    dp[0] = 1;
    l[0] = r[0] = l[1] = r[1] = 1;
    for (int i = 1; i <= n; i++) {
        int mi = A[i];
        int f = i & 1;
        insert(i & 1, A[i], dp[i - 1]);
        dp[i] = (sum[f] - sum[1 - f] + P) % P;
        if (i > 1) ans = (dp[i] - ans + P) % P;
    }
    printf("%d\n", ans);
    return 0;
}

T3 集合划分

　　直接输出“-1”没有分  差评。。

正解：

　　

#include<bits/stdc++.h>
#define gc getchar()
#define pc putchar
using namespace std;
typedef long long li;
const int M = 300005;
bool fg[M], vst[M], pt[20];
int n, m, k, mx, a[10010];
int h, t, ft, st[20];
int q[M], f[M], tj[M], lst[M];
int as[M];
li s1 = 19260817, s2 = 23333333;
li s3 = 998244853, srd;

li read() {
    li x = 0, y = 0, c = gc;
    while (!isdigit(c)) y = c, c = gc;
    while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ '0'), c = gc;
    return y == '-' ? -x : x;
}

void print(li q) {
    if (q < 0) {
        pc('-');
        q = -q;
    }
    if (q >= 10) print(q / 10);
    pc(q % 10 + '0');
}

li rd() {
    return srd = (srd * s1 + s2 + rand()) % s3;
}

int main() {
    srand(time(0));
    rd();
    int i, j, l;
    n = read(); m = read(); k = read();
    mx = (1 << n) - 1;
    for (i = 1; i <= m; ++i)
        a[i] = read(), f[a[i]] = a[i];
    if (m > k) return puts("-1"), 0;
    for (i = 1; i <= mx; ++i)
        tj[i] = tj[i >> 1] + (i & 1);
    for (i = 1; i <= mx; i <<= 1)
        for (j = 0; j <= mx; j += (i << 1))
            for (l = j; l < j + i; ++l)
                f[l + i] |= f[l];
    int q1 = 0, q2 = 0;
    for (i = 0; i <= mx; ++i) fg[i] = 1;
    for (i = 1; i <= n; ++i) {
        if (k & (1 << n - i)) ++q1;
        else ++q2;
        for (j = 0; j <= mx; ++j)
            if (n - tj[j] == q1 && tj[j] - tj[f[j]] < q2)
                fg[j] = 0;
    }
    if (!fg[mx]) {
        puts("-1");
        return 0;
    }
    int nw, nxt;
    q[++t] = mx;
    vst[mx] = 1;
    while (h < t) {
        nw = q[++h];
        for (i = 1; i <= n; ++i)
            if (nw & (1 << i - 1)) {
                nxt = nw ^ (1 << i - 1);
                if (!fg[nxt] || vst[nxt]) continue;
                vst[nxt] = 1;
                lst[nxt] = nw;
                q[++t] = nxt;
            }

    }
    if (!vst[0]) {
        puts("-1");
        return 0;
    }
    for (nw = 0; nw != mx; nw = lst[nw])
        st[++ft] = nw;
    st[++ft] = mx;
    for (i = 1; i <= n; ++i) {
        if (k & (1 << n - i)) {
            while (pt[ft - 1]) --ft;
            nw = st[ft] ^ st[ft - 1];
            --ft;
            for (j = 1; j <= mx; ++j)
                if (!as[j] && (j & nw)) as[j] = 2;
        }
        else {
            l = 0;
            for (j = 1; j <= m; ++j)
                if (!as[a[j]]) l |= a[j];
            for (j = 1; j < ft; ++j)
                if (!pt[j] && ((st[j] ^ st[j + 1]) & l) == 0) {
                    nw = st[j] ^ st[j + 1];
                    pt[j] = 1;
                    break;
                }
            for (j = 1; j <= mx; ++j)
                if (!as[j] && (j & nw)) as[j] = 1;
        }
    }
    for(i = 1; i <= mx; ++i)
        pc(as[i] - 1 + '0');
    pc('\n');
    return 0;
}