开学第六测
开学第六测
又一次考试... 成绩出来后心情无比的down
为什么??因为爆零了 2333
每次考完试都会发题解 但是被点名必须要写之后,就不是很想写了
接下来是正题:
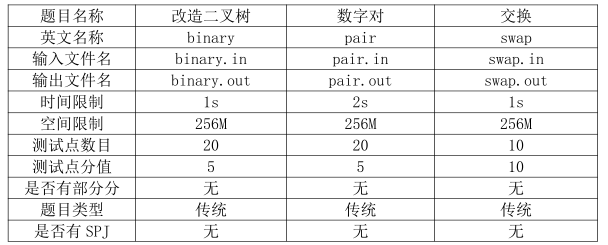
T1 期望得分:20??
(本题相当于 洛谷 P3365)
【题目描述】
小Y在学树论时看到了有关二叉树的介绍:在计算机科学中,二叉树是每个结点最多有两个子结点的有序树。通常子结点被称作“左孩子”和“右孩子” 。二叉树被用作二叉搜索树和二叉堆。随后他又和他人讨论起了二叉搜索树。
什么是二叉搜索树呢?二叉搜索树首先是一棵二叉树。设key[p]表示结点p上的数值。对于其中的每个结点p,若其存在左孩子lch,则key[p]>key[lch];若其存在右孩子rch, 则key[p]<key[rch];注意,本题中的二叉搜索树应满足对于所有结点,其左子树中的key小于当前结点的key,其右子树中的key大于当前结点的key。
小Y与他人讨论的内容则是,现在给定一棵二叉树,可以任意修改结点的数值。修改一个结点的数值算作一次修改,且这个结点不能再被修改。若要将其变成一棵二叉搜索树, 且任意时刻结点的数值必须是整数(可以是负整数或0) ,所要的最少修改次数。
相信这一定难不倒你!请帮助小Y解决这个问题吧。
【 输入格式】
第一行一个正整数 n 表示二叉树结点数。结点从 1~n 进行编号。
第二行 n 个正整数用空格分隔开,第 i 个数 ai 表示结点 i 的原始数值。
此后 n - 1 行每行两个非负整数 fa, ch,第 i + 2 行描述结点 i + 1 的父亲编号 fa,以及父子关系 ch,(ch = 0 表示 i + 1 为左儿子,ch = 1 表示 i + 1 为右儿子)。
结点 1 一定是二叉树的根。
【 输出格式】
仅一行包含一个整数,表示最少的修改次数。
【 样例输入】
3
2 2 2
1 0
1 1
【 样例输出】
2
【 数据范围】
20 % :n <= 10 , ai <= 100.
40 % :n <= 100 , ai <= 200
60 % :n <= 2000 .
100 % :n <= 10 ^ 5 , ai < 2 ^ 31.
思路:20% :暴力。
40% :可以用 DP 或者贪心或者神奇的暴力等其他奇怪的方法完成。
60% :正解的 LIS 打成 O(n ^ 2)。
100% :首先求出这颗二叉树的中序遍历,那么问题就转换成用最少的修改次数使这个整数序列严格单调递增。于是很自然的想到了 LIS,但单纯用 LIS 是有一些问题的,比如这种情况:2 3 1 4, LIS 为 2 3 4,答案求出来为 1,但由于整数的限制,应该要修改 2 次。即直接 LIS 求出的答案是在非严格递增的情况下的答案。所以我们将原序列稍加修改,一个常见的将严格递增整数序列映射成非严格递增整数序列的技巧就是将如下序列:
a1, a2, a3, a4 ... an 映射成:
a1 - 1, a2 - 2, a3 - 3, a4 - 4 ... an - n. (这种方法常见于计数类问题)。
这样映射后求最长不下降子序列的长度就没问题了。

#include <algorithm> #include <iostream> #include <cstring> #include <cstdio> #include <cmath> using namespace std; const int N = 1e5 + 3; int n, fa, d, sum, qr, l, r, mid, top, stk[N], f[N], a[N], b[N], lc[N], rc[N]; bool vis[N]; char ch; int read() { while (ch = getchar(), ch < '0' || ch > '9'); int res = ch - 48; while (ch = getchar(), ch >= '0' && ch <= '9') res = res * 10 + ch - 48; return res; } void Bfs() { int x; stk[top = 1] = 1; while (top) { x = stk[top]; if (lc[x] && !vis[lc[x]]) { stk[++top] = lc[x]; continue; } b[++sum] = a[x]; b[sum] -= sum; vis[x] = true; --top; if (rc[x] && !vis[rc[x]]) { stk[++top] = rc[x]; continue; } } return ; } int main() { // freopen("binary.in", "r", stdin); // freopen("binary.out", "w", stdout); n = read(); for (int i = 1; i <= n; ++i) a[i] = read(); for (int i = 2; i <= n; ++i) { fa = read(); d = read(); (d ? rc[fa] : lc[fa]) = i; } Bfs(); f[qr = 1] = b[1]; for (int i = 2; i <= n; ++i) { if (b[i] >= f[qr]) f[++qr] = b[i]; else { l = 1; r = qr; while (l <= r) { mid = l + r >> 1; if (f[mid] <= b[i]) l = mid + 1; else r = mid - 1; } f[l] = b[i]; } } cout << n - qr << endl; // fclose(stdin); fclose(stdout); return 0; }
T2 期望得分:30 or 60 ??
【题目描述】
小 H 是个善于思考的学生,现在她又在思考一个有关序列的问题。
她的面前浮现出一个长度为 n 的序列{ai},她想找出一段区间[L, R](1 <= L <= R <= n)。
这个特殊区间满足,存在一个 k(L <= k <= R),并且对于任意的 i(L <= i <= R),ai 都能被 ak 整除。这样的一个特殊区间 [L, R]价值为 R - L。
小 H 想知道序列中所有特殊区间的最大价值是多少,而有多少个这样的区间呢?这些区间又分别是哪些呢?你能帮助她吧。
【 输入格式】
第一行,一个整数 n.
第二行,n 个整数,代表 ai.
【 输出格式】
第一行两个整数,num 和 val,表示价值最大的特殊区间的个数以及最大价值。
第二行 num 个整数,按升序输出每个价值最大的特殊区间的 L.
【 样例输入1】
5
4 6 9 3 6
【 样例输出1】
1 3
2
【 样例输入2】
5
2 3 5 7 11
【 样例输出2】
5 0
1 2 3 4 5
【 数据范围】
30 % : 1 <= n <= 30 , 1 <= ai <= 32.
60 % :1 <= n <= 3000 , 1 <= ai <= 1024.
80 % : 1 <= n <= 300000 , 1 <= ai <= 1048576.
100 % :1 <= n <= 500000 , 1 <= ai < 2 ^ 31.
思路1:30% :暴力枚举判断。O(n^4)。
60% :特殊区间的特点实际上就是区间最小值等于这个区间的 GCD,于是暴力或递推算出每个区间的最小值与 GCD。而对于最大价值,可以通过二分来进行求解。复杂度 O(n^2)。
100%:在 60%的基础上,最小值与 GCD 都使用 RMQ 算法来求解,对于这道题推荐使用ST 表。最大价值仍然使用二分。复杂度 O(nlogn)。
思路2:因为 L <= k <= R,所以可以从每一个数开始向前、向后扩展,计算有多少个数可以被这个数整除。
例:数列 24 12 6 5 8 7 中,从6向前扩展时,12可以被6整除,而在扩展12时已知24能被12整除,所以6也能扩展到24。
那么每个数只需要被扩展一次即可,整体思路有些类似于记忆化,时间复杂度是比思路1更优的,是O(n)。
思路3:线段树维护每个区间的GCD,然后二分( 好像AC不了)

#include <algorithm> #include <iostream> #include <cstring> #include <cstdio> #include <cmath> using namespace std; const int N = 5e5 + 3, M = 21; int n, m, a, ans, l, r, mid, sum; int A[N], f[N][M], g[N][M], p[M]; inline int Gcd(const int &x, const int &y) { return y == 0 ? x : Gcd(y, x % y); } bool check(int len) { int q = log2(len--), k = n + 1 - p[q], j; for (int i = 1; i <= k; ++i) { j = i + len; if (min(f[i][q], f[j - p[q] + 1][q]) == Gcd(g[i][q], g[j - p[q] + 1][q])) return true; } return false; } char ch; inline int read() { while (ch = getchar(), ch < '0' || ch > '9'); int res = ch - 48; while (ch = getchar(), ch >= '0' && ch <= '9') res = res * 10 + ch - 48; return res; } char s[10]; inline void print(int x) { int res = 0; if (x == 0) putchar('0'); while (x) { s[++res] = x % 10; x /= 10; } for (int i = res; i; --i) putchar(s[i] + '0'); putchar(' '); return ; } int main() { // freopen("pair.in", "r", stdin); // freopen("pair.out", "w", stdout); n = read(); m = log2(n); for (int i = 1; i <= n; ++i) { a = read(); f[i][0] = g[i][0] = a; } for (int i = 0; i <= m; ++i) p[i] = 1 << i; for (int j = 1; j <= m; ++j) { int k = n + 1 - p[j]; for (int i = 1; i <= k; ++i) { f[i][j] = min(f[i][j - 1], f[i + p[j - 1]][j - 1]); g[i][j] = Gcd(g[i][j - 1], g[i + p[j - 1]][j - 1]); } } l = 1; r = n; while (l <= r) { mid = l + r >> 1; if (check(mid)) l = mid + 1; else r = mid - 1; } ans = r; if (ans == 1) { printf("%d %d\n", n, 0); for (int i = 1; i < n; ++i) print(i); printf("%d\n", n); } else { int q = log2(ans--), k = n + 1 - p[q], j; for (int i = 1; i <= k; ++i) { j = i + ans; if (min(f[i][q], f[j - p[q] + 1][q]) == Gcd(g[i][q], g[j - p[q] + 1][q])) A[++sum] = i; } printf("%d %d\n", sum, ans); for (int i = 1; i < sum; ++i) print(A[i]); printf("%d\n", A[sum]); } // fclose(stdin); fclose(stdout); return 0; }

#include<cstring> #include<cstdio> #include<cmath> using namespace std; const int MAXN = 1e6 + 10; int N, a[MAXN]; int ans[MAXN], mx, L[MAXN], R[MAXN], happen[MAXN]; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9'){if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } void GetL(int now) { int cur = now; while(cur >= 1 && a[cur] % a[now] == 0) L[now] = L[cur], cur = L[cur] - 1; } void GetR(int now) { int cur = now; while(cur <= N && a[cur] % a[now] == 0) R[now] = R[cur], cur = R[cur] + 1; } int main() { // freopen("pair.in", "r", stdin); // freopen("pair.out", "w", stdout); N = read(); for(int i = 1; i <= N; i++) a[i] = read(); for(int i = 1; i <= N; i++) { L[i] = i; GetL(i); } for(int i = N; i >= 1; i--) { R[i] = i; GetR(i); } for(int i = 1; i <= N; i++) { ans[i] = R[i] - L[i]; if(ans[i] > mx) mx = ans[i]; } int num = 0; for(int i = 1; i <= N; i++) if(ans[i] == mx && !happen[L[i]]) num++, happen[L[i]] = 1; memset(happen, 0, sizeof(happen)); printf("%d %d\n", num, mx); for(int i = 1; i <= N; i++) if(ans[i] == mx && !happen[L[i]]) printf("%d ", L[i]), happen[L[i]] = 1; // fclose(stdin); fclose(stdout); return 0; }

#include<iostream> #include<cstdio> #include<map> #define N 1000005 using namespace std; int gcd(int i, int j) { return j ? gcd(j, i % j) : i; } map<int, int> ma; int n, k[N]; int tot, ans, sum; int t[N << 2]; int Answer[N]; void build(int l, int r, int ret) { if(l == r) { t[ret] = k[l]; return ; } int mid = (l+r) >> 1; build(l, mid, ret << 1); build(mid+1, r, ret << 1 | 1); t[ret] = gcd(t[ret << 1], t[ret << 1 | 1]); } int query(int l, int r, int ret, int L, int R) { if(l>=L && r<=R) return t[ret]; int mid = (l+r) >> 1; if(L<=mid && R>mid) return gcd(query(l, mid, ret << 1, L, R), query(mid+1, r, ret << 1 | 1, L, R)); if(L<=mid) return query(l, mid, ret << 1, L, R); if(R>mid) return query(mid+1, r, ret << 1 | 1, L, R); } bool check(int mid){ int tmp; for(int i = 1; i + mid <= n; ++i){ tmp = query(1, n, 1, i, i + mid); if(tmp>1 && ma.find(tmp) != ma.end()) { ans = max(ans, mid); return true; } } return false; } int main(){ // freopen("pair.in","r",stdin); // freopen("pair.out","w",stdout); scanf("%d", &n); for(int i = 1; i <= n; ++i) { scanf("%d", &k[i]); ma[k[i]] = ++tot; } build(1, n, 1); int l = 1, r = n, mid; while(l <= r) { mid = (l+r) >> 1; if(check(mid)) l = mid+1; else r = mid-1; } int tmp, num = 0; for(int i = 1; i+ans <= n; ++i) { tmp = query(1, n, 1, i, i + mid); if(ma.find(tmp)!=ma.end() || ans==0) { Answer[++num] = i; } } printf("%d %d\n", num, ans); for(int i = 1; i <= number; ++i) printf("%d ", Answer[i]); putchar('\n'); // fclose(stdin); fclose(stdout); return 0; }
T3 期望得分:0 (连题目都没看懂 2333)
【 题目描述】
给定一个{0, 1, 2, 3, … , n - 1}的排列 p。一个{0, 1, 2 , … , n - 2}的排列 q 被认为是优美的排列,当且仅当 q 满足下列条件:
对排列 s = {0, 1, 2, 3, ..., n - 1}进行 n – 1 次交换。
1. 交换 s[q0],s[q0 + 1]
2. 交换 s[q1],s[q1 + 1]
.....
最后能使得排列 s = p.
问有多少个优美的排列,答案对 10^9+7 取模。
【 输入格式】
第一行,一个整数 n.
第二行 ,n 个整数代表排列 p.
【 输出格式】
仅一行表示答案。
【 样例输入】
3
1 2 0
【 样例输出】
1
【样例解释】
q = {0,1} {0,1,2} ->{1,0,2} -> {1, 2, 0}
q = {1,0} {0,1,2} ->{0,2,1} -> {2, 0, 1}
【 数据范围】
30 % : 1 <= n <= 10.
100 % :1 <= n <= 50.
思路:30%:枚举所有排列,判定即可
100%:考虑倒着处理, 比如交换 (i, i + 1), 那么前面的所有数不管怎么交换都无法到后面去(下标恒小于等于 i),后面的数也是一样到不了前面。说明这最后一次交换前,就要求对于所有的 x <= i, y > i,px < py。所以交换前左边的数是连续的,右边也是连续的。由于交换前, 前面和后面的数是互相不干涉的, 所以就归结成了两个子问题。 于是我们可以用记忆化搜索来解决这个问题。
设 dp[ n ][ low ] 代表长度为 n,H 是{ low, low + 1, …, low + n - 1 }的排列,且 H 是 p 的子序列,在 H 上优美序列的个数。
我们枚举交换哪两个相邻元素( k, k+1 ), 然后判断 k 前面的所有数是否都小于后面的所有数,如果是则进行转移 dp[ n ][ low ] += dp[ k ][ low ] * dp[ n – k ][ low + k ] * C( n – 2, n – 1 - k )。即前面的 k 个元素与后面的 n - k 个元素是两个独立的子问题,前面是{ low ... low + k - 1 }的排列,后面是{ low + k ... low + n - 1 }的排列,C( n - 2, n - 1 - k)代表的是在交换( k, k + 1 )前左右两边还分别要进行 n - 2 次交换,而每次交换左边与交换右边是不同方案,这相当于 n - 2个位置选择 n - 1 - k 个位置填入,故还需要乘上 C( n - 2, n - 1 - k )。时间复杂度为 O( n^4 )。

#include<algorithm> #include<iostream> #include<cstring> #include<cstdio> #define MAXN 51 #define mod 1000000007 using namespace std; int n, ans; int vis[MAXN]; int p[MAXN], q[MAXN], s[MAXN]; int judge() { for(int i = 0; i < n; i++) s[i] = i; for(int i = 0; i < n-1; i++) swap(s[q[i]], s[q[i]+1]); for(int i = 0; i < n; i++) if(s[i] != p[i]) return false; return true; } void dfs(int tot) { if(tot == n-1){ if(judge()) ans++; return ; } for(int i = 0; i < n;i++) if(!vis[i]) { vis[i] = 1; q[tot] = p[i]; dfs(tot + 1); vis[i] = 0; } } int main() { // freopen("swap.in","r",stdin); // freopen("swap.out","w",stdout); scanf("%d", &n); for(int i = 0; i < n; i++) scanf("%d", &p[i]); dfs(0); printf("%d\n", ans % mod); // fclose(stdin); fclose(stdout); }

#include <algorithm> #include <iostream> #include <cstring> #include <cstdio> #include <cmath> using namespace std; typedef long long ll; const int N = 52, Mod = 1e9 + 7; int n, p[N], dp[N][N], C[N][N]; int Dfs(int len, int low) { if(dp[len][low] != -1) return dp[len][low]; if(len == 1) return dp[len][low] = 1; int &res = dp[len][low]; res = 0; int t[N], m = 0, j, k; for(int i = 1; i <= n; ++i) if(p[i] >= low && p[i] < low + len) t[++m] = p[i]; for(int i = 1; i < m; ++i) { swap(t[i], t[i + 1]); for(j = 1; j <= i; ++j) if (t[j] >= low + i) break; for(k = i + 1; k <= m; ++k) if (t[k] < low + i) break; if(j > i && k > m) { ll tmp = (ll)Dfs(i, low) * Dfs(m - i, low + i) % Mod; tmp = tmp * C[m - 2][i - 1] % Mod; res = (res + tmp) % Mod; } swap(t[i], t[i + 1]); } return res; } int main() { // freopen("swap.in", "r", stdin); // freopen("swap.out", "w", stdout); scanf("%d", &n); for(int i = 1; i <= n; ++i) scanf("%d", &p[i]); memset(dp, -1, sizeof(dp)); for(int i = 0; i <= n; ++i) { C[i][0] = 1; for(int j = 1; j <= i; ++j) C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % Mod; } Dfs(n, 0); if(dp[n][0] != -1) cout << dp[n][0] << endl; else puts("0"); // fclose(stdin); fclose(stdout); return 0; }





