不忘初心，方得始终
关于导数的一些知识
——记一次远程讲课
定义：
f ( x ) 是一个函数，它的导数记为 f ' ( x )
导数 f ' ( x ) 即为函数 f ( x ) 在函数图像中的斜率
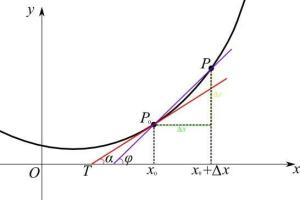
导函数的定义式即为：( f( x + Δx ) - f( x ) ) / ( ( x + Δx ) - x )
相当于取函数中的两个点( x1, y1), ( x2, y2 ), 那式子为： ( y2 - y1 ) / ( x2 - x1 )
首先，我们来讲讲极限：
lim x -> x0 f(x)，表示 f(x)这个函数在x0这个点的极限。
（lim 只是一种记法罢了，是拉丁语 limes 的缩写，差不多是极限的意思，但不要认为是 limit ，让人笑话哦）
表达的意思很简单，就是当 x 的取值 “无限接近” x0 的时候，f(x)的值是多少。比如 f(x) = x 在 x->0 的时候就是 0 。
当然 极限是可能不存在的。比如 lim x->0 1 / x 。
大家应该知道的，当 x 无限趋向 0 ，函数值是无穷大，注意无穷大并不一定是极限不存在的唯一情况，还有一些情况比如 分段函数 在间断点的极限是不存在的。比如 f(x) = x+1 如果 x > 0= x - 1 如果 x < 0 x->0，因为-1也是对的1也是对的。
这个事实上叫 左极限不等于右极限，也就是x从数轴左边靠近0和从右边靠近，得到的函数值是不一样的。
接下来我们来说点新东西：
我们为了表达 “很小” 这个概念，引入一个新的符号 dx。我们只要感性理解他,不要去具体思考背后数学是啥。
我们可以简单理解 dx 就是一个很小很小的值，比如 lim x->1 f(x) = x，我们同样可以写成 lim dx -> 0 f(1 + dx)。
然后，我们来做题吧
哦对了，一般我们写下dx的时候，默认了dx是 -> 0，当然这个表达不大精确，但是我们可以方便写一些数学式子。
dx / dx = ？
dx / 1 = ？
当看到 dx / 1 就自动想成, lim x-> 0 x / 1就行了，所以 dx / dx 就是 lim x->0 x / x，所以 dx / dx = 1，或者说他们都等于 0。其实，就按照 lim x->0 x / x算就行。
下一个问题有点麻烦 (dx)^2 / dx = ? ，即 lim x->0 x^2/x = ？
当然是都等于 0 啦。
其实是想说明一个很重要的概念：无穷小 是有 “阶” 的。(dx)^2 被称为 2阶无穷小 ，就是说 它比 dx 更小一点，dx^2 / dx一下，就只有0了。
接下来就要应用我们一开始说的导数的定义及其定义式了：
f(x) = x^2 的导数是什么呢？
这时就有小盆友要问了：“是不是要求它的斜率呢？但是二次函数的我不会求啊 2333。。。”
这时就需要使用定义式了。将 f(x) = x^2 代入定义式 ( f(x + dx) - f(x)) / ((dx + x) - x) ，答案为 dx + 2x ，又因为 lim dx -> 0，所以，答案应为 2x 。（如图）
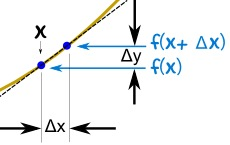
从几何上来说大概就是这个意思：当你取得两个点 无限接近，斜率就等于 2x
好，下一题
f(x) = cos(x) 的导数是什么呢？？ （@_@）
再次请出定义式，so... f'(x) = - sin(x) 你有没有做对呢？？
PS：此处要补充一个知识：sin(dx) 近似于 dx
推导过程：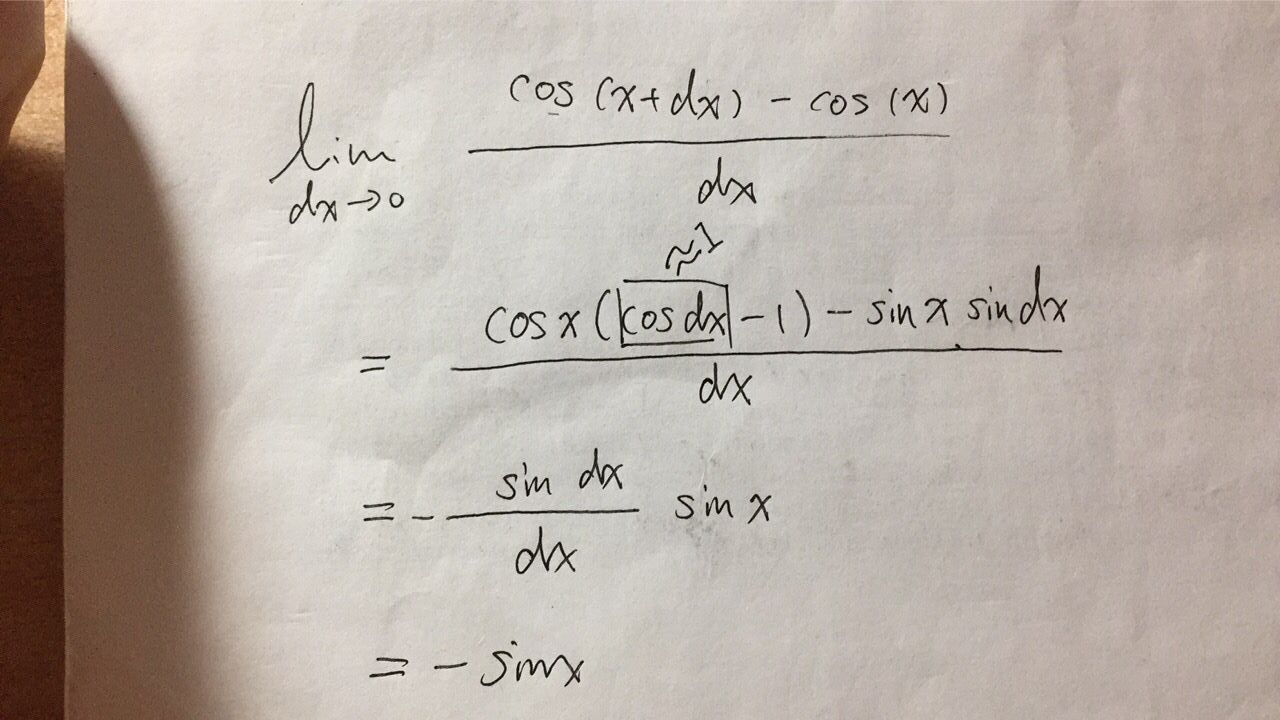
老师的字很漂酿 是吧是吧 (*￣︶￣)
接下来是思考题：
T：我们来思考一个问题 f'(x) = 0说明什么？？
M：说明 x 是常数
T: 如果只是某个点是0呢？？
M: 斜率是0
T: 说明啥 （老师快忍不了了 2333）
M: @_@ 凌乱ing
T: 好吧， 说明x是一个 f(x)的极值点，极大值/极小值。嗯...比如我们来求一下 f(x) = ax^2 + bx + c 的导数。
M: 2ax+b
T: f‘(x) = 0 的解是什么
M: - b / 2a （大家有没有发现什么呢）
T: 嗯。所以 求导数 可以用来求函数的极值，不过 极值和“最值”是不一样的哦。有一个定理，一个函数的最大/最小值 一定出现在 端点处 或者 极值处。应该很好理解吧
（ENDING：我觉得接下来的东西你基本 都能看懂了，记得如果有想不明白的就回到 定义上，想想是怎么算这些函数的导数的（就像是 不忘初心，方得始终）。我觉得你应该 网上的东西 都能看懂了。嗯 还有就是 极值点不一定是最值点，极值点可以用 f'(x) = 0 找到）
