程序员编程艺术第十六~第二十章：全排列，跳台阶，奇偶调序等问题

第十六~第二十章：全排列，跳台阶，奇偶排序，第一个只出现一次等问题

作者：July、2011.10.16。
出处：http://blog.csdn.net/v_JULY_v。

引言

    最近这几天闲职在家，一忙着投简历，二为准备面试而搜集整理各种面试题。故常常关注个人所建的Algorithms1-14群内朋友关于笔试，面试，宣讲会，offer，薪资的讨论以及在群内发布的各种笔/面试题，常感言道：咱们这群人之前已经在学校受够了学校的那种应试教育，如今出来找工作又得东奔西走去参加各种笔试/面试，着实亦不轻松。幻想，如果在企业与求职者之间有个中间面试服务平台就更好了。

    ok，闲话少扯。在上一篇文章中，已经说过，“个人正在针对那100题一题一题的写文章，多种思路，不断优化，即成程序员编程艺术系列。”现本编程艺术系列继续开始创作，你而后自会和我有同样的感慨：各种面试题千变万化，层出不穷，但基本类型，解决问题的思路基本一致。

    本文为程序员编程艺术第十六章~第二十章，包含以下5个问题：

1. 全排列；
2. 跳台阶；
3. 奇偶排序；
4. 第一个只出现一次的字符；
5. 一致性哈希算法。

    同时，本文会在解答去年微软面试100题的部分题目时，尽量结合今年最近各大IT公司最新的面试题来讲解，两相对比，彼此对照，相信你会更加赞同我上面的话。且本文也不奢望读者能从中学到什么高深技术之类的东西，只求读者看此文看着舒服便可，通顺流畅以致一口气读完而无任何压力。ok，有任何问题，欢迎不吝指正。谢谢。

第一部分、全排列问题

53.字符串的排列。
题目：输入一个字符串，打印出该字符串中字符的所有排列。
例如输入字符串abc，则输出由字符a、b、c 所能排列出来的所有字符串
abc、acb、bac、bca、cab 和cba。

    分析：此题最初整理于去年的微软面试100题中第53题，第二次整理于微软、Google等公司非常好的面试题及解答[第61-70题] 第67题。无独有偶，这个问题今年又出现于今年的2011.10.09百度笔试题中。ok，接下来，咱们先好好分析这个问题。

• 一、递归实现
  从集合中依次选出每一个元素，作为排列的第一个元素，然后对剩余的元素进行全排列，如此递归处理，从而得到所有元素的全排列。以对字符串abc进行全排列为例，我们可以这么做：以abc为例
  固定a，求后面bc的排列：abc，acb，求好后，a和b交换，得到bac
  固定b，求后面ac的排列：bac，bca，求好后，c放到第一位置，得到cba
  固定c，求后面ba的排列：cba，cab。代码可如下编写所示：

template <typename T>
void CalcAllPermutation_R(T perm[], int first, int num)
{
    if (num <= 1) {
        return;
    }

    for (int i = first; i < first + num; ++i) {
        swap(perm[i], perm[first]);
        CalcAllPermutation_R(perm, first + 1, num - 1);
        swap(perm[i], perm[first]);
    }
}

    或者如此编写，亦可：void Permutation(char* pStr, char* pBegin); void Permutation(char* pStr) { Permutation(pStr, pStr); } void Permutation(char* pStr, char* pBegin) { if(!pStr || !pBegin) return; if(*pBegin == '\0') { printf("%s\n", pStr); } else { for(char* pCh = pBegin; *pCh != '\0'; ++ pCh) { // swap pCh and pBegin char temp = *pCh; *pCh = *pBegin; *pBegin = temp; Permutation(pStr, pBegin + 1); // restore pCh and pBegin temp = *pCh; *pCh = *pBegin; *pBegin = temp; } } }

• 二、字典序排列
  把升序的排列（当然，也可以实现为降序）作为当前排列开始，然后依次计算当前排列的下一个字典序排列。
  对当前排列从后向前扫描，找到一对为升序的相邻元素，记为i和j（i < j）。如果不存在这样一对为升序的相邻元素，则所有排列均已找到，算法结束；否则，重新对当前排列从后向前扫描，找到第一个大于i的元素k，交换i和k，然后对从j开始到结束的子序列反转，则此时得到的新排列就为下一个字典序排列。这种方式实现得到的所有排列是按字典序有序的，这也是C++ STL算法next_permutation的思想。算法实现如下：

template <typename T>
void CalcAllPermutation(T perm[], int num)
{
    if (num < 1)
        return;

    while (true) {
        int i;
        for (i = num - 2; i >= 0; --i) {
            if (perm[i] < perm[i + 1])
                break;
        }

        if (i < 0)
            break;  // 已经找到所有排列

        int k;
        for (k = num - 1; k > i; --k) {
            if (perm[k] > perm[i])
                break;
        }

        swap(perm[i], perm[k]);
        reverse(perm + i + 1, perm + num);

    }
}

  扩展：如果不是求字符的所有排列，而是求字符的所有组合，应该怎么办呢？当输入的字符串中含有相同的字符串时，相同的字符交换位置是不同的排列，但是同一个组合。举个例子，如果输入abc，它的组合有a、b、c、ab、ac、bc、abc。

第二部分、跳台阶问题

27.跳台阶问题
题目：一个台阶总共有n 级，如果一次可以跳1 级，也可以跳2 级。
求总共有多少总跳法，并分析算法的时间复杂度。

    分析：在九月腾讯，创新工场，淘宝等公司最新面试十三题中第23题又出现了这个问题，题目描述如下：23、人人笔试1：一个人上台阶可以一次上1个，2个，或者3个，问这个人上n层的台阶，总共有几种走法？咱们先撇开这个人人笔试的问题（其实差别就在于人人笔试题中多了一次可以跳三级的情况而已），先来看这个第27题。

    首先考虑最简单的情况。如果只有1级台阶，那显然只有一种跳法。如果有2级台阶，那就有两种跳的方法了：一种是分两次跳，每次跳1级；另外一种就是一次跳2级。

    现在我们再来讨论一般情况。我们把n级台阶时的跳法看成是n的函数，记为f(n)。当n>2时，第一次跳的时候就有两种不同的选择：一是第一次只跳1级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目，即为f(n-1)；另外一种选择是第一次跳2级，此时跳法数目等于后面剩下的n-2级台阶的跳法数目，即为f(n-2)。因此n级台阶时的不同跳法的总数f(n)=f(n-1)+(f-2)。

    我们把上面的分析用一个公式总结如下：
        /  1                             n=1
f(n)=      2                          n=2
        \  f(n-1)+(f-2)            n>2

    原来上述问题就是我们平常所熟知的Fibonacci数列问题。可编写代码，如下：

long long Fibonacci_Solution1(unsigned int n) { int result[2] = {0, 1}; if(n < 2) return result[n]; return Fibonacci_Solution1(n - 1) + Fibonacci_Solution1(n - 2); }

     那么，如果是人人笔试那道题呢?一个人上台阶可以一次上1个，2个，或者3个，岂不是可以轻而易举的写下如下公式：

        /      1                                      n=1
f(n)=      2                                      n=2

              4                                      n=3       //111, 12, 21, 3
        \  f(n-1)+(f-2)+f(n-3)            n>3

    行文至此，你可能会认为问题已经解决了，但事实上没有：

1. 用递归方法计算的时间复杂度是以n的指数的方式递增的，我们可以尝试用递推方法解决。具体如何操作，读者自行思考。
   
2. 有一种方法，能在O(logn)的时间复杂度内求解Fibonacci数列问题，你能想到么?
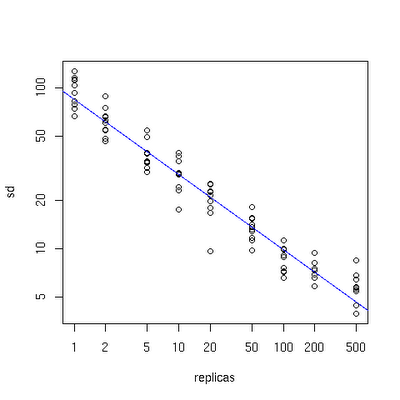
3. 同时，有朋友指出对于这个台阶问题只需求幂就可以了（求复数幂C++库里有），不用任何循环且复杂度为O（1），如下图所示，是否真如此?：

第三部分、奇偶调序

54.调整数组顺序使奇数位于偶数前面。
题目：输入一个整数数组，调整数组中数字的顺序，使得所有奇数位于数组的前半部分，
所有偶数位于数组的后半部分。要求时间复杂度为O(n)。

分析：

1. 你当然可以从头扫描这个数组，每碰到一个偶数时，拿出这个数字，并把位于这个数字后面的所有数字往前挪动一位。挪完之后在数组的末尾有一个空位，这时把该偶数放入这个空位。由于碰到一个偶数，需要移动O(n)个数字，只是这种方法总的时间复杂度是O(n^２)，不符合要求，pass。
   
2. 很简单，维护两个指针，一个指针指向数组的第一个数字，向后移动；一个个指针指向最后一个数字，向前移动。如果第一个指针指向的数字是偶数而第二个指针指向的数字是奇数，我们就交换这两个数字。
   

    思路有了，接下来，写代码实现：//思路，很简答，俩指针，一首一尾 //如果第一个指针指向的数字是偶数而第二个指针指向的数字是奇数， //我们就交换这两个数字 // 2 1 3 4 6 5 7 // 7 1 3 4 6 5 2 // 7 1 3 5 6 4 2 //如果限制空间复杂度为O（1），时间为O（N），且奇偶数之间相对顺序不变，就相当于正负数间顺序调整的那道题了。 //copyright@2010 zhedahht。 void Reorder(int *pData, unsigned int length, bool (*func)(int)); bool isEven(int n); void ReorderOddEven(int *pData, unsigned int length) { if(pData == NULL || length == 0) return; Reorder(pData, length, isEven); } void Reorder(int *pData, unsigned int length, bool (*func)(int)) { if(pData == NULL || length == 0) return; int *pBegin = pData; int *pEnd = pData + length - 1; while(pBegin < pEnd) { // if *pBegin does not satisfy func, move forward if(!func(*pBegin)) //偶数 { pBegin ++; continue; } // if *pEnd does not satisfy func, move backward if(func(*pEnd)) //奇数 { pEnd --; continue; } // if *pBegin satisfy func while *pEnd does not, // swap these integers int temp = *pBegin; *pBegin = *pEnd; *pEnd = temp; } } bool isEven(int n) { return (n & 1) == 0; }

    细心的读者想必注意到了上述程序注释中所说的“如果限制空间复杂度为O（1），时间为O（N）就相当于正负数间顺序调整的那道题了”，没错，它与个人之前整理的一文中的第5题极其类似：5、一个未排序整数数组，有正负数，重新排列使负数排在正数前面，并且要求不改变原来的正负数之间相对顺序 比如： input: 1,7,-5,9,-12,15 ans: -5,-12,1,7,9,15 要求时间复杂度O(N),空间O(1) 。（此题一直没看到令我满意的答案，一般达不到题目所要求的：时间复杂度O(N),空间O(1)，且保证原来正负数之间的相对位置不变）。

    如果你想到了绝妙的解决办法，不妨在本文评论下告知于我，或者来信指导（zhoulei0907@yahoo.cn），谢谢。

第四部分、第一个只出现一次的字符

第17 题：题目：在一个字符串中找到第一个只出现一次的字符。如输入abaccdeff，则输出b。

    分析：这道题是2006 年google 的一道笔试题。它在今年又出现了，不过换了一种形式。即最近的搜狐笔试大题：数组非常长，如何找到第一个只出现一次的数字，说明算法复杂度。此问题已经在程序员编程艺术系列第二章中有所阐述，在此不再作过多讲解。

代码，可编写如下：

#include <iostream>
using namespace std;

//查找第一个只出现一次的字符，第1个程序
//copyright@ Sorehead && July
//July、updated，2011.04.24.
char find_first_unique_char(char *str)
{
    int data[256];
    char *p;

    if (str == NULL)
        return '\0';

    memset(data, 0, sizeof(data));    //数组元素先全部初始化为0
    p = str;
    while (*p != '\0')
        data[(unsigned char)*p++]++;  //遍历字符串，在相应位置++，（同时，下标强制转换）

    while (*str != '\0')
    {
        if (data[(unsigned char)*str] == 1)  //最后，输出那个第一个只出现次数为1的字符
            return *str;

        str++;
    }

    return '\0';
}

int main()
{
    char *str = "afaccde";
    cout << find_first_unique_char(str) << endl;
    return 0;
}

  当然，代码也可以这么写（测试正确）： 

//查找第一个只出现一次的字符，第2个程序
//copyright@ yansha
//July、updated，2011.04.24.
char FirstNotRepeatChar(char* pString)
{
    if(!pString)
        return '\0';

    const int tableSize = 256;
    int hashTable[tableSize] = {0}; //存入数组，并初始化为0

    char* pHashKey = pString;
    while(*(pHashKey) != '\0')
        hashTable[*(pHashKey++)]++;

    while(*pString != '\0')
    {
        if(hashTable[*pString] == 1)
            return *pString;

        pString++;
    }
    return '\0';  //没有找到满足条件的字符，退出
}

第五部分、一致性哈希算法

tencent2012笔试题附加题
    问题描述： 例如手机朋友网有n个服务器，为了方便用户的访问会在服务器上缓存数据，因此用户每次访问的时候最好能保持同一台服务器。
已有的做法是根据ServerIPIndex[QQNUM%n]得到请求的服务器，这种方法很方便将用户分到不同的服务器上去。但是如果一台服务器死掉了，那么n就变为了n-1，那么ServerIPIndex[QQNUM%n]与ServerIPIndex[QQNUM%（n-1）]基本上都不一样了，所以大多数用户的请求都会转到其他服务器，这样会发生大量访问错误。

    问： 如何改进或者换一种方法，使得：
（1）一台服务器死掉后，不会造成大面积的访问错误，
（2）原有的访问基本还是停留在同一台服务器上；
（3）尽量考虑负载均衡。（思路：往分布式一致哈希算法方面考虑。）

1. 最土的办法还是用模余方法：做法很简单，假设有N台服务器，现在完好的是M（M<=N),先用N求模，如果不落在完好的机器上，然后再用N-1求模，直到M.这种方式对于坏的机器不多的情况下，具有更好的稳定性。
   
2. 一致性哈希算法。

    下面，本文剩下部分重点来讲讲这个一致性哈希算法。

应用场景

    在做服务器负载均衡时候可供选择的负载均衡的算法有很多，包括：  轮循算法（Round Robin）、哈希算法（HASH）、最少连接算法（Least Connection）、响应速度算法（Response Time）、加权法（Weighted ）等。其中哈希算法是最为常用的算法.

    典型的应用场景是： 有N台服务器提供缓存服务，需要对服务器进行负载均衡，将请求平均分发到每台服务器上，每台机器负责1/N的服务。

    常用的算法是对hash结果取余数 (hash() mod N)：对机器编号从0到N-1，按照自定义的hash()算法，对每个请求的hash()值按N取模，得到余数i，然后将请求分发到编号为i的机器。但这样的算法方法存在致命问题，如果某一台机器宕机，那么应该落在该机器的请求就无法得到正确的处理，这时需要将当掉的服务器从算法从去除，此时候会有(N-1)/N的服务器的缓存数据需要重新进行计算；如果新增一台机器，会有N /(N+1)的服务器的缓存数据需要进行重新计算。对于系统而言，这通常是不可接受的颠簸（因为这意味着大量缓存的失效或者数据需要转移）。那么，如何设计一个负载均衡策略，使得受到影响的请求尽可能的少呢？
    在Memcached、Key-Value Store、Bittorrent DHT、LVS中都采用了Consistent Hashing算法，可以说Consistent Hashing 是分布式系统负载均衡的首选算法。

Consistent Hashing算法描述

    下面以Memcached中的Consisten Hashing算法为例说明。

    由于hash算法结果一般为unsigned int型，因此对于hash函数的结果应该均匀分布在[0,2³²-1]间，如果我们把一个圆环用2³² 个点来进行均匀切割，首先按照hash(key)函数算出服务器（节点）的哈希值， 并将其分布到0～2³²的圆上。

    用同样的hash(key)函数求出需要存储数据的键的哈希值，并映射到圆上。然后从数据映射到的位置开始顺时针查找，将数据保存到找到的第一个服务器（节点）上。

 

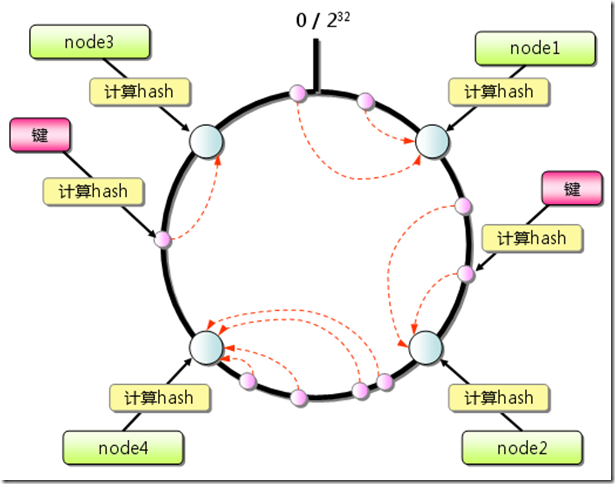
Consistent Hashing原理示意图

    新增一个节点的时候，只有在圆环上新增节点逆时针方向的第一个节点的数据会受到影响。删除一个节点的时候，只有在圆环上原来删除节点顺时针方向的第一个节点的数据会受到影响，因此通过Consistent Hashing很好地解决了负载均衡中由于新增节点、删除节点引起的hash值颠簸问题。

   

Consistent Hashing添加服务器示意图

    虚拟节点（virtual nodes）：之所以要引进虚拟节点是因为在服务器（节点）数较少的情况下（例如只有3台服务器），通过hash(key)算出节点的哈希值在圆环上并不是均匀分布的（稀疏的），仍然会出现各节点负载不均衡的问题。虚拟节点可以认为是实际节点的复制品（replicas），本质上与实际节点实际上是一样的（key并不相同）。引入虚拟节点后，通过将每个实际的服务器（节点）数按照一定的比例(例如200倍)扩大后并计算其hash(key)值以均匀分布到圆环上。在进行负载均衡时候，落到虚拟节点的哈希值实际就落到了实际的节点上。由于所有的实际节点是按照相同的比例复制成虚拟节点的，因此解决了节点数较少的情况下哈希值在圆环上均匀分布的问题。

 

                 虚拟节点对Consistent Hashing结果的影响

    从上图可以看出，在节点数为10个的情况下，每个实际节点的虚拟节点数为实际节点的100-200倍的时候，结果还是很均衡的。

 

    “但这样的算法方法存在致命问题，如果某一台机器宕机，那么应该落在该机器的请求就无法得到正确的处理，这时需要将当掉的服务器从算法从去除，此时候会有(N-1)/N的服务器的缓存数据需要重新进行计算；”

为何是 (N-1)/N 呢？解释如下：

  比如有 3 台机器，hash值 1-6 在这3台上的分布就是：

  host 1: 1 4

  host 2: 2 5

  host 3: 3 6

  如果挂掉一台，只剩两台，模数取 2 ，那么分布情况就变成：

  host 1: 1 3 5

  host 2: 2 4 6

    可以看到，还在数据位置不变的只有2个： 1，2，位置发生改变的有4个，占共6个数据的比率是 4/6 = 2/3，这样的话，受影响的数据太多了，势必太多的数据需要重新从 DB 加载到 cache 中，严重影响性能。

后记

1. 以上部分代码思路有参考自此博客：http://zhedahht.blog.163.com/blog/。特此注明下。     
2. 行文仓促，若有任何问题或漏洞，欢迎不吝指正或赐教。谢谢。转载，请注明出处。完。