目标检测 | Farthest Point Sampling 及其 CUDA 实现
Farthest Point Sampling 及其 CUDA 实现
概述
在深度学习中,在mesh模型(网格模型)上直接学习并预测是一个相当复杂的任务,一方面在于没有高效的模型,另一方面在于现实中难以直接获取性质良好的mesh模型。所以我们常会通过采样和扫描的形式将mesh模型或者现实中的物体转化为point cloud(点云),对于一个点云,其定义为一个\(N\times C\)的张量,\(N\)表示有多少个点,\(C\)表示每个点的信息。对于一个三维的点云,一般\(C=3\),以表示\((x,y,z)\)。如果点云还携带了更多的信息例如反射强度等,则\(C=3+C^\prime\)。而评价这个点云质量的好坏,就是评价这个点云是否尽可能保留了mesh模型中的几何特征。
现在假设我们拥有一个mesh模型,其渲染效果如下图所示:
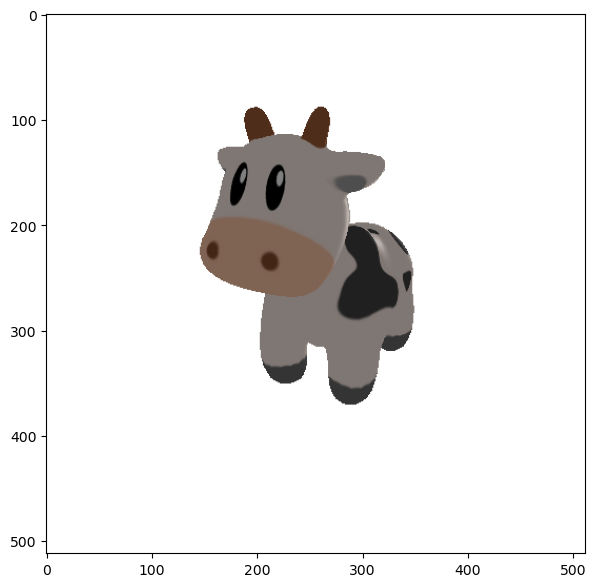
但是我们的模型不能直接处理这个mesh模型,因此我们通过扫描或者采样的方式得到了一组\(4096\times 3\)的点云:
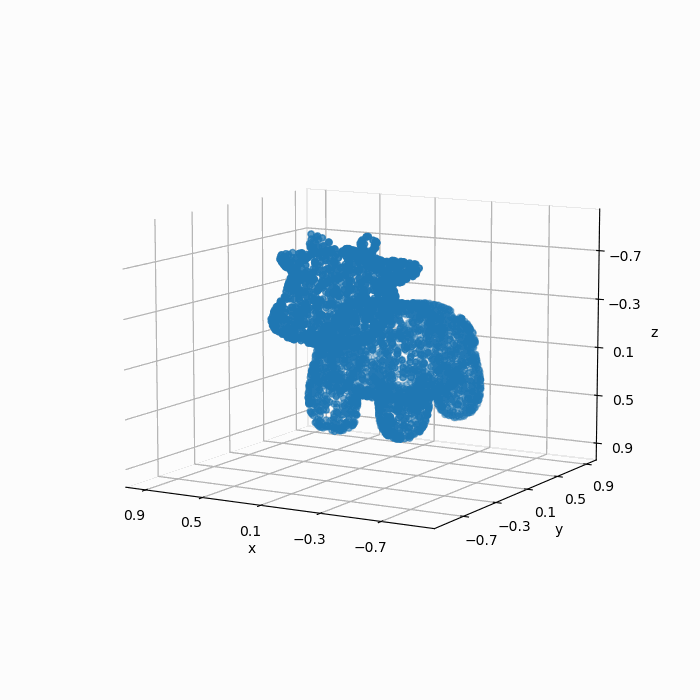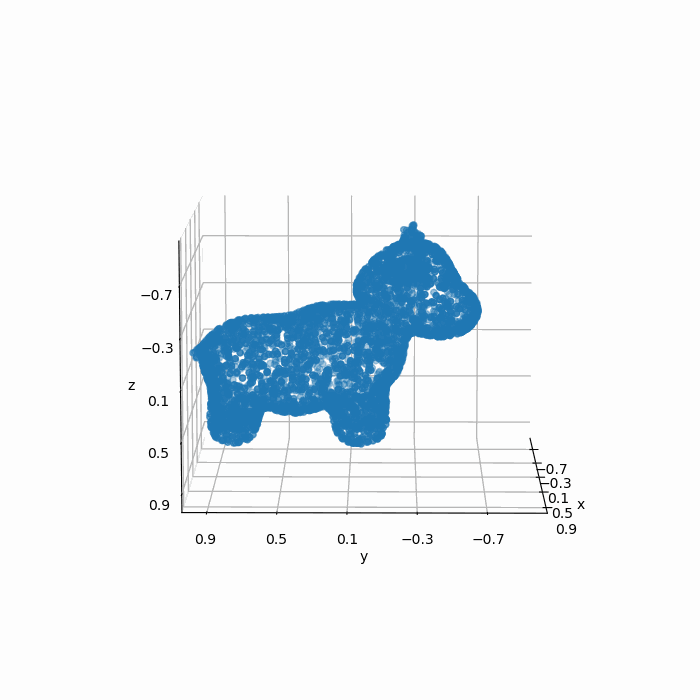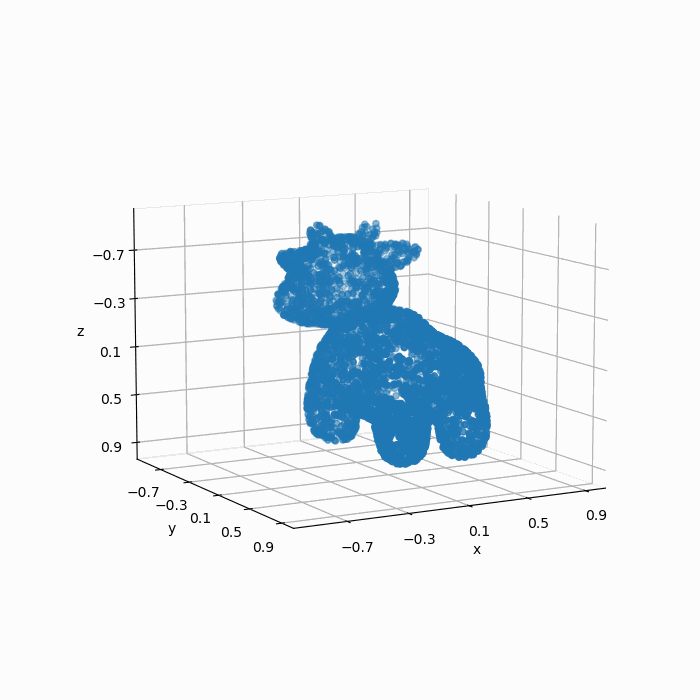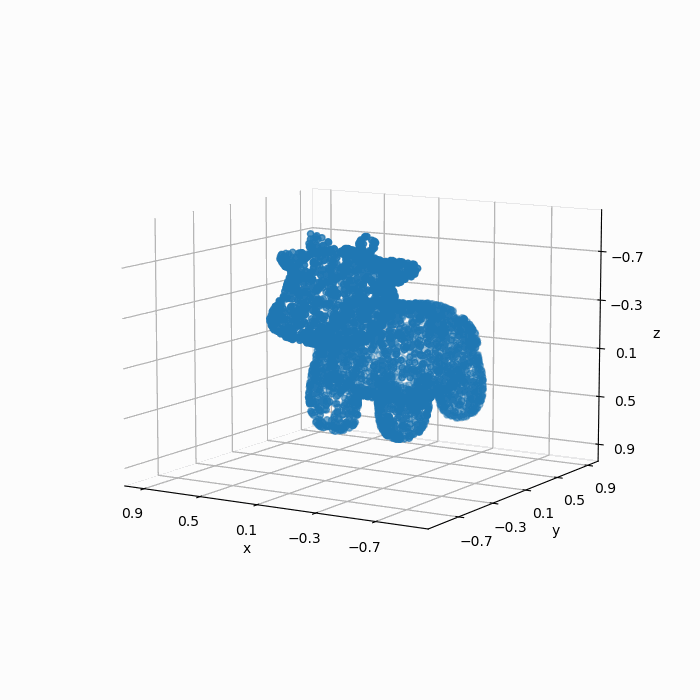
如果我们凭借肉眼观察,可见这组点云较好地保留了mesh的几何特征,因此这组点云可以称得上是“质量不错”。
但是我们需要把这组\(4096\times 3\)点云输入到一个输入为固定大小\(256\times 3\)的模型中,我们就必须通过下采样将点云采样为\(256\times 3\)。
均匀随机采样
首先我们想到的一种最为朴素的下采样方法就是均匀随机采样(uniform random sampling),这种下采样方法在python中可以被简单实现:
# 所有的点(1 x 4096 x 3)
total_point = ...
# 进行均匀随机采样
num_samples = 256
indices = torch.randint(0, total_point.size(1), (num_samples,))
sampled_points = total_point[0, indices]
# 可视化
plot_pointcloud(sampled_points, title="uniform random sampling")
plt.show()
我们得到采样结果为:
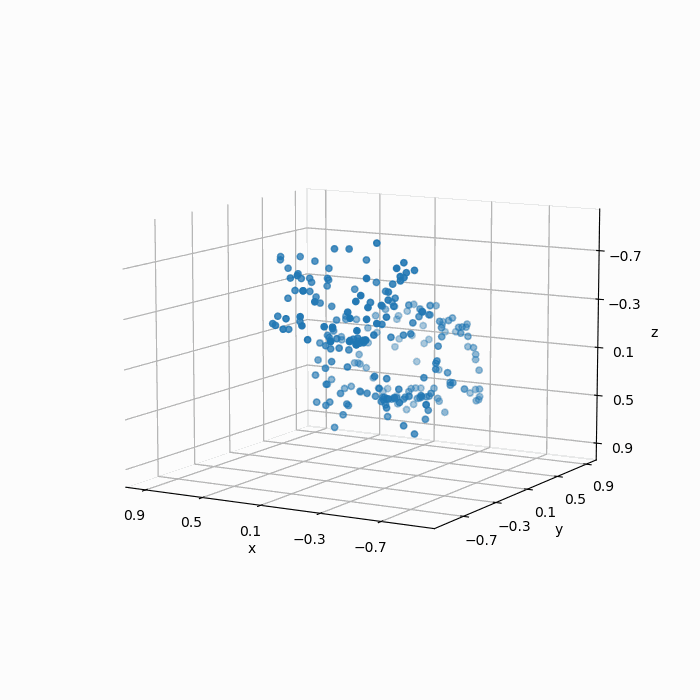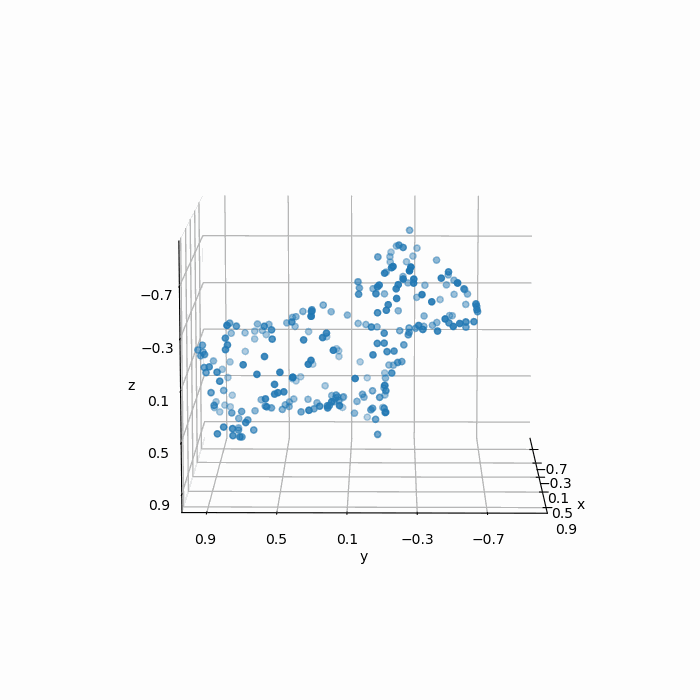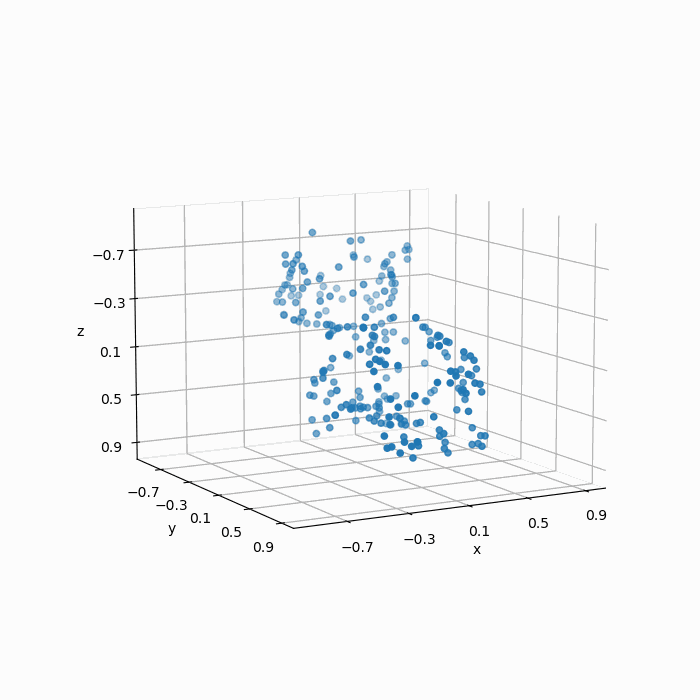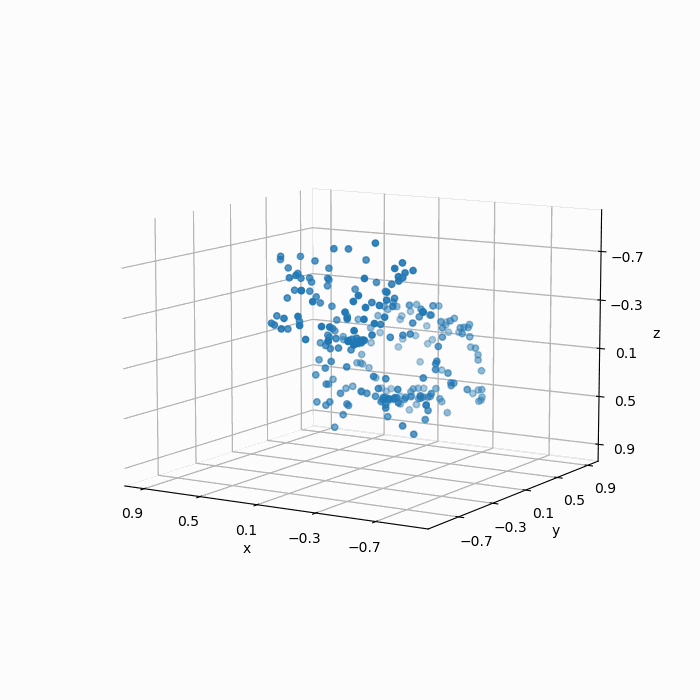
显然这组点云的采样效果并不能称得上“质量不错”,如下图所示,经过采样之后的点并不能很好地保留原始的几何特征,显然均匀随机采样得到的点在分布上却并不均匀。
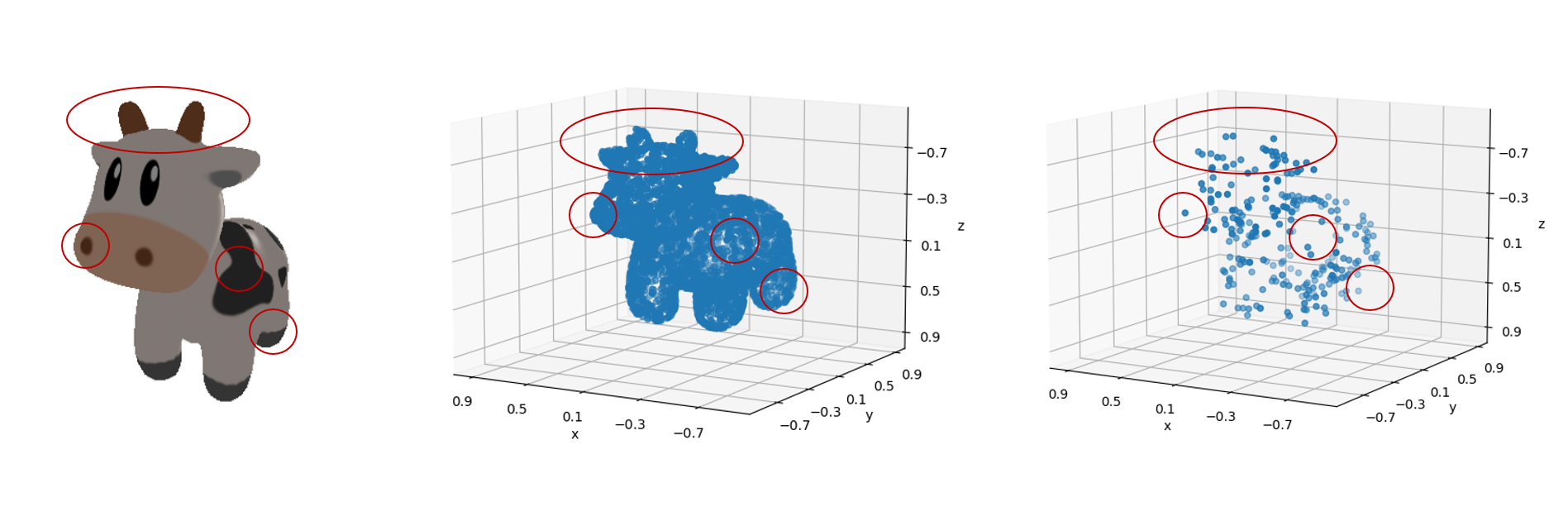
经过简单分析,这是因为曲率更大的表面,其几何细节更多,但是在均匀随机采样中,高曲率表面的点与低曲率表面的点权重一致,导致了在曲率更大的表面上,采样的失真程度更高。
Farthest Point Sampling
Farthest Point Sampling (FPS)最早被引入深度学习领域应该是Charles R. Qi等人的文章PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space,FPS算法在其中作为PointNet++特征提取的中心点采样层使用。
FPS算法的本质是贪心算法,其基本思想是从点云中选择一个起始点,然后在剩余的点中选择与已选点距离最远的点作为下一个选定点。这个过程迭代进行,直到达到所需数量的采样点为止。通过这种方式,FPS确保了选定的点在整个点云中分布均匀,从而能够较好地表示点云的特征。
FPS的关键步骤包括:
- 选择起始点: 从点云中随机选择一个点作为起始点。
- 计算距离: 计算剩余点与已选点之间的距离。
- 选择最远点: 选择距离已选点最远的点作为下一个选定点。
- 重复步骤2和步骤3: 重复计算距离和选择最远点的过程,直到达到所需数量的采样点。
如下图所示,在每一次循环迭代的开始,我们有已采样的点集(红色点),尚未被采样的点集(绿色点)。其中我们可以将红色点连接起来,可以看做一个流形(虚线),可以看到距离这个流形表面越远的绿色点,其曲率将会越大,拥有的几何细节也就越多,所以我们在迭代中将距离最远的绿色点加入已采样集合中。通过这种贪心算法的思想,我们确保每次采样都是最高几何细节保留。
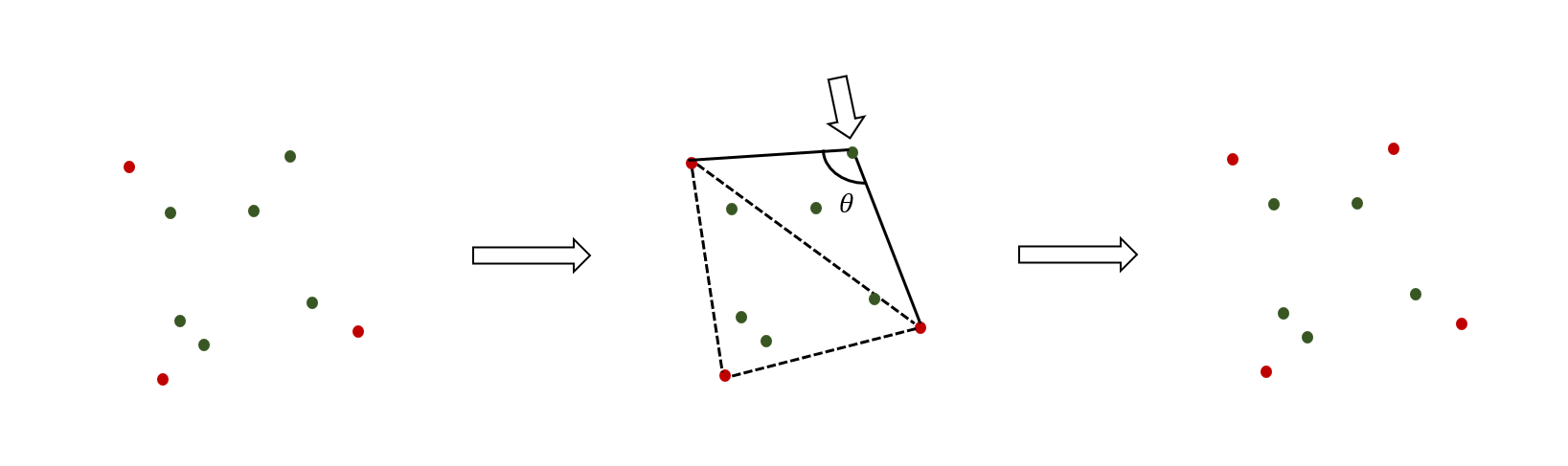
我们可以写出每次迭代的数学描述:
其中\(P\)是点云,为\(N\times C\)的张量,\(S\)是采样得到的点集索引,\(d(x,y)\)是距离函数。
根据上述数学描述,我们可以写出FPS算法的CPU实现:
def farthest_point_sampling(points:torch.Tensor, num_samples:int):
"""
使用Farthest Point Sampling (FPS)算法从点云中选择一组关键点。
参数:
- points (torch.Tensor): 输入点云,每一行是一个点的坐标。
- num_samples (int): 要选择的采样点的数量。
返回:
- selected_points (torch.Tensor): 选择的关键点的坐标。
"""
num_points = points.size(0)
selected_indices = points.new_empty(num_samples, dtype=torch.long)
distances = points.new_ones(num_points) * float('inf')
# 从输入点云中随机选择一个起始点
start_index = 0
selected_indices[0] = start_index
selected_point = points[start_index]
# 迭代选择最远点
for i in range(1, num_samples):
# 计算每个点与已选点之间的欧几里得距离
dist_to_selected = torch.norm(points - selected_point, dim=1)
# 更新距离,选择最远点
distances = torch.min(distances, dist_to_selected)
farthest_index = torch.argmax(distances)
selected_indices[i] = farthest_index
selected_point = points[farthest_index]
selected_points = points[selected_indices]
return selected_points
如下图所示,FPS算法得到结果明显要比均匀随机采样的“质量”更好:
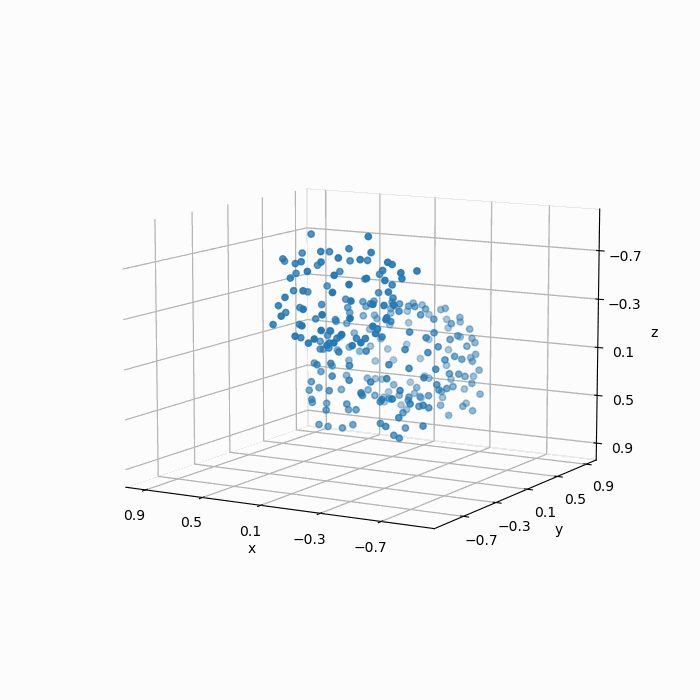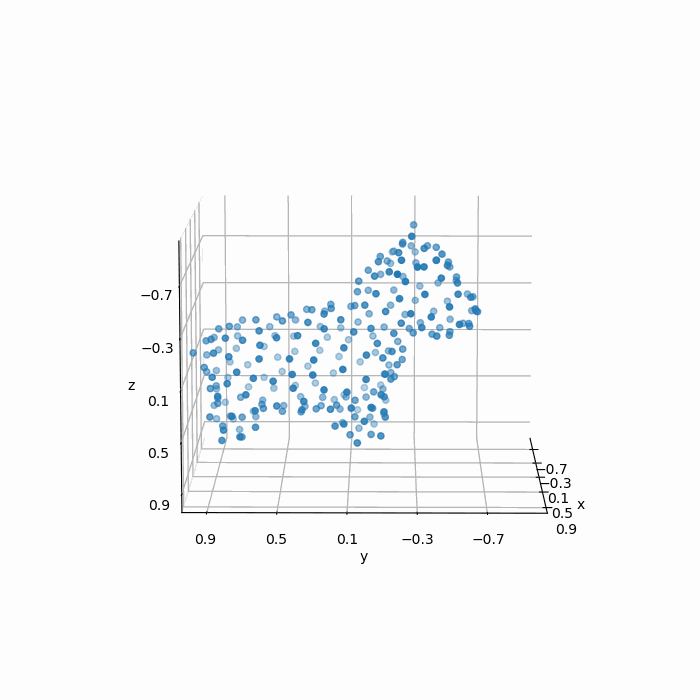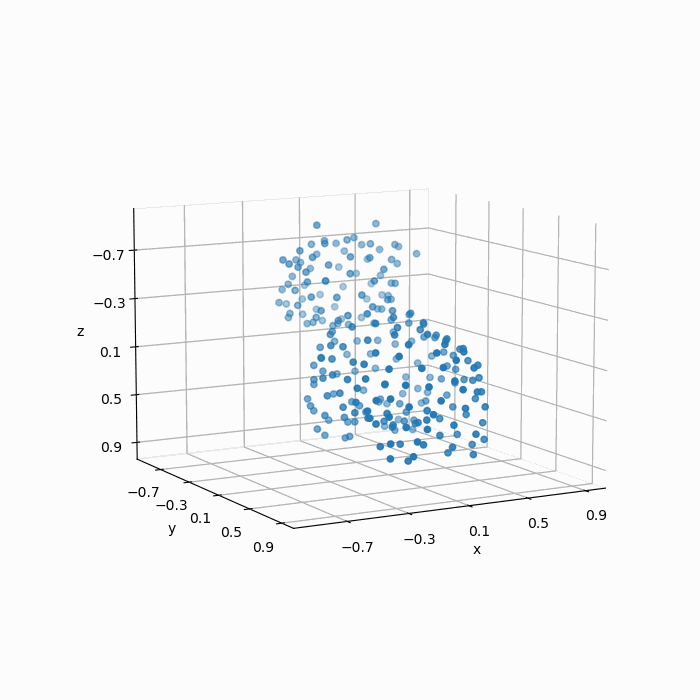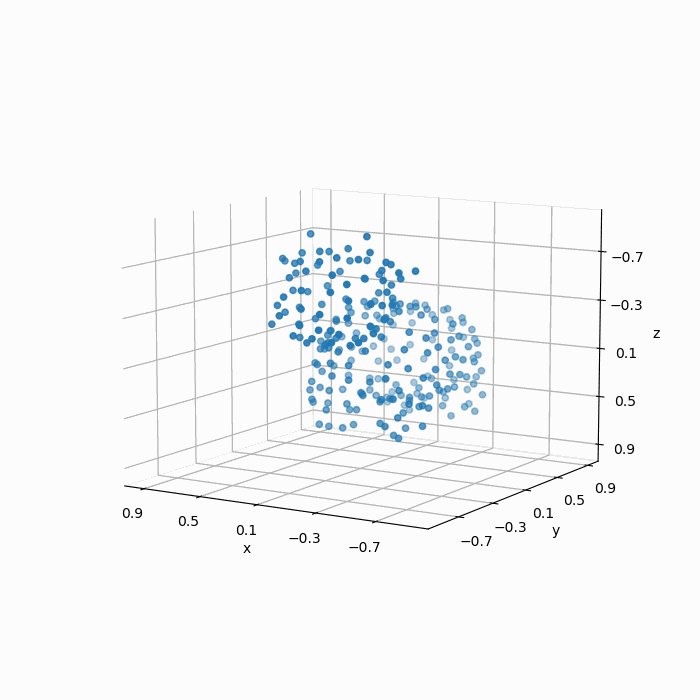
最后,我们再对比一下原始图像(a),采样结果(b),均匀随机采样(c)以及FPS采样(d):
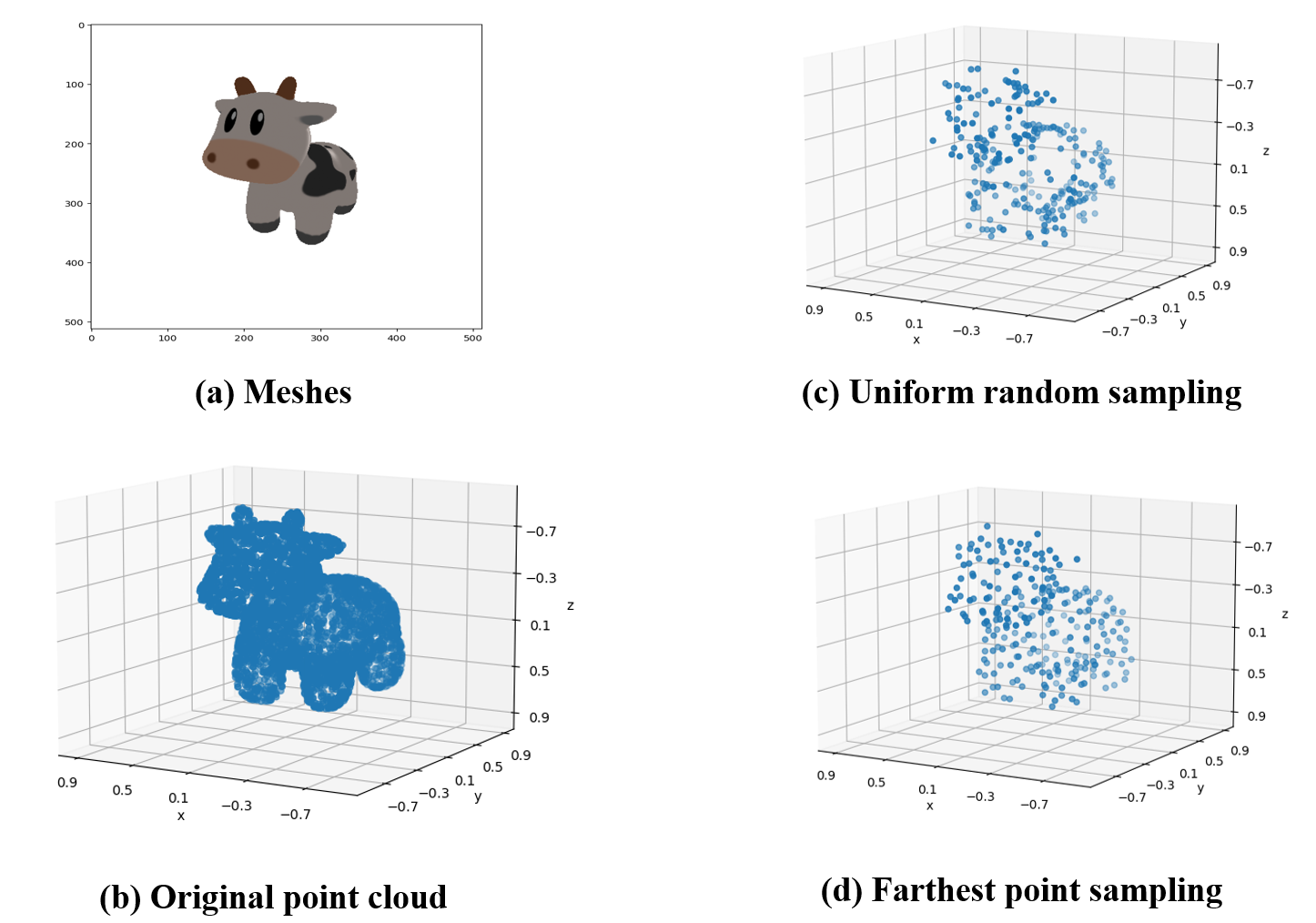
Farthest Point Sampling 的并行版本
在上一节中,我们给出了FPS算法的数学描述:
其中\(P\)是点云,为\(N\times C\)的张量,\(S\)是采样得到的点集索引,\(d(x,y)\)是距离函数。
其中
可以被写成并行的版本
注意到\(p_k = \text{argmax}_{p \in \text{P}} D_k\)需要前一步操作的线程同步,所以形成了算法中的一个瓶颈
当然在实际操作中,CUDA核心提供的thread数目有限(单个block的大小有限),为了方便对齐,我们往往会将点云划分为多个子集。每个thread都可以看作一个分治的分支,在内部串行地计算分配给它的子集,最后在线程同步阶段完成所有子集的归并
我们以实际中使用最多的FPS算法CUDA实现为例进行解读,源码可以在这里找到:
整段代码可以被划分为两个部分,其中第二部分还可以划分为子集计算与子集归并:
- 参数初始化
- 循环采样
- 子集计算
- 子集归并
参数初始化
如下述代码所示,这段代码负责为thread开辟内存,计算当前batch id以及确定当前thread的id,并确定起始点(设为0)
if (m <= 0) return;
__shared__ float dists[block_size];
__shared__ int dists_i[block_size];
int batch_index = blockIdx.x;
dataset += batch_index * n * 3;
temp += batch_index * n;
idxs += batch_index * m;
int tid = threadIdx.x;
const int stride = block_size;
int old = 0;
if (threadIdx.x == 0) idxs[0] = old;
__syncthreads();
子集计算
循环采样分为外循环与内循环,外循环是一个\((1,M)\)的循环,其中\(M\)是采样的点数量。
内循负责计算当前迭代的距离,我们为每个thread分配一个子集,其子集的定义为:
,其中\(S\)为block的thread数量,\(\text{thread}_\text{id}\)为当前trhread的id。
例如当\(S=512\)时,\(id\)为\(0\)则\(\text{thread}_0=\{0,512,1024,\cdots\}\),\(id\)为\(1\)则\(\text{thread}_1=\{1,513,1025,\cdots\},\cdots\)
随后求出每个thread中的最大距离,即:
for (int j = 1; j < m; j++) {
int besti = 0;
float best = -1;
float x1 = dataset[old * 3 + 0];
float y1 = dataset[old * 3 + 1];
float z1 = dataset[old * 3 + 2];
for (int k = tid; k < n; k += stride) {
float x2, y2, z2;
x2 = dataset[k * 3 + 0];
y2 = dataset[k * 3 + 1];
z2 = dataset[k * 3 + 2];
float mag = (x2 * x2) + (y2 * y2) + (z2 * z2);
if (mag <= 1e-3) continue;
float d =
(x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1) + (z2 - z1) * (z2 - z1);
float d2 = min(d, temp[k]);
temp[k] = d2;
besti = d2 > best ? k : besti;
best = d2 > best ? d2 : best;
}
dists[tid] = best;
dists_i[tid] = besti;
__syncthreads();
}
子集归并
完成所有的\(\text{best}_k\)的计算之后,进入子集归并阶段。这里的子集归并是一个硬编码的二路归并,归并规则如下:
例如,当thread数量\(S=512\),第一轮\(n=256\)
算法将归并\(\text{best}_0\)与\(\text{best}_{256}\),\(\text{best}_1\)与\(\text{best}_{257}\),\(\text{best}_2\)与\(\text{best}_{258}\),\(\cdots\),\(\text{best}_{255}\)与\(\text{best}_{511}\)。
经过第一轮归并后,子集数量减半,只剩下\(256\)个子集。
同理继续归并,直到只剩下最后一个子集\(\text{best}_0\),将\(\text{best}_0\)的点并入已采样点集中,完成一轮采样。
if (block_size >= 512) {
if (tid < 256) {
__update(dists, dists_i, tid, tid + 256);
}
__syncthreads();
}
if (block_size >= 256) {
if (tid < 128) {
__update(dists, dists_i, tid, tid + 128);
}
__syncthreads();
}
if (block_size >= 128) {
if (tid < 64) {
__update(dists, dists_i, tid, tid + 64);
}
__syncthreads();
}
if (block_size >= 64) {
if (tid < 32) {
__update(dists, dists_i, tid, tid + 32);
}
__syncthreads();
}
if (block_size >= 32) {
if (tid < 16) {
__update(dists, dists_i, tid, tid + 16);
}
__syncthreads();
}
if (block_size >= 16) {
if (tid < 8) {
__update(dists, dists_i, tid, tid + 8);
}
__syncthreads();
}
if (block_size >= 8) {
if (tid < 4) {
__update(dists, dists_i, tid, tid + 4);
}
__syncthreads();
}
if (block_size >= 4) {
if (tid < 2) {
__update(dists, dists_i, tid, tid + 2);
}
__syncthreads();
}
if (block_size >= 2) {
if (tid < 1) {
__update(dists, dists_i, tid, tid + 1);
}
__syncthreads();
}
old = dists_i[0];
if (tid == 0) idxs[j] = old;
综上所述,并行版本的FPS算法将时间复杂度从\(O(MN)\)压缩为\(O(M\frac{N}{S})\),其中\(M\)为采样数目,\(N\)为待采样点云大小,\(S\)为thread数量(单个block的大小)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号