UE5模拟交互篇｜可交互流体风场实现

【USparkle专栏】如果你深怀绝技，爱“搞点研究”，乐于分享也博采众长，我们期待你的加入，让智慧的火花碰撞交织，让知识的传递生生不息！

一、原理介绍

1. 思路分析
先来说观察介质模拟的两种视角：拉格朗日视角和欧拉视角。

拉格朗日视角一般将介质视为粒子（或微小网格）的集合，粒子会随着介质一起移动，通过计算每个粒子的运动状态和受力情况来表现介质的变化。欧拉视角则通常将介质占有的空间切分为一个个小网格，对每个小格子计算格子内介质的状态、输入输出情况，以及对其他的格子的影响。

要计算某一位置点的风力，如果采用拉格朗日视角，就需要获得单位时间内经过该位置点的平均粒子速度，这样显然不太现实，因为单位时间内经过该点的粒子概率较低。如果采用欧拉视角，只需要查找该点所位于的格子位置，进而可以直接读出平均速度。

在2019年的GDC上《战神》的风场技术分享也是基于欧拉视角下实现的。

《战神》可交互风场分享

局部速度场

玩家的行为可以影响到速度场的变化，而速度场又可以给场景中的物体施加力的作用。

《战神》中的做法是划分32x32x16米的区域，精度为1米每个格子记录该格子内的平均速度，并且整个速度场会跟随角色移动，对场景交互产生的影响也只会发生在该区域范围内。超过范围内的直接采样噪声或者给一个默认速度，这样网格就不要遍布整个世界空间来达到节省开支。

既然知道了整个风场是建立在场的基础下，那么玩家是如何影响到场，而场又怎样进行符合现实中的物理规则的变化？这就不得不提这篇名为《Real-Time Fluid Dynamics for Games》的经典论文。

2. 解析论文

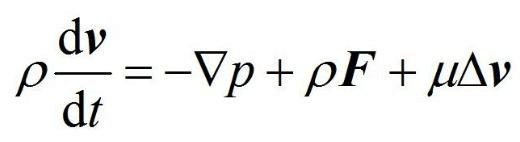
纳维-斯托克斯方程

Stable Fluids的基础是Navier-Stokes方程组，是作为流体模拟的首选。这里的流体是不可压缩（Incompressible）流体，也就是密度、温度不变。其中P是压力场（标量场），p表示密度，v表示粘滞系数（Viscosity），F是外力。

N-S通式（1）中可变形为

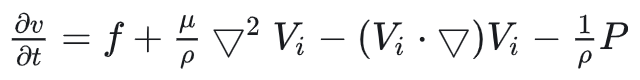
第一项F很好理解，表示外力。对应论文中的AddSource项，表示加在速度场中的外力，在游戏中流体交互主要体现在对外力的施加上。

第二项论文中的扩散项，可以简单理解成液体的粘稠性质，该项表示速度在自身二阶导下扩散。扩散越强烈，场就越平滑。欧拉视角下表示为每个单元和周围的邻域交换。理想情况下的交换可表示为：

理想情况下单元格流体之间交换

x = x0 + a*(sum_p – num*x0)*dt

其中x0表示先前状态，x为当前状态，a为扩散速率，num为相邻单元格数量，sum_p和sum_c分别为相邻单元格前一时刻的和后一时刻值的总和。

论文作者认为第二项直接求可能为负，会产生摇摆和发散，所以不这么做。因此他对式子进行如下变形：

x0 = x - a*(sum_c – num*x)*dt
x0= x – a*sum_c*dt + a*num*x*dt
(1 + a*num*dt)x = x0 + a*sum_c*dt
x = (x0 + a*sum_c*dt)/(1 + a*num*dt)

论文中认为对这个求解没必要进行求逆，而作者用到了Gauss-Seidel Relaxation方法，对方程组进行迭代多次，逐步逼近。

第三项对应论文中的对流项（Advect），速度会沿着自身的方向运动。可以理解成流体的速度会导致流体随流动一起传输物体、密度和其他量。这时可以把流体想象成一个个粒子随着速度运动，作者在论文中使用了半拉格朗日方法：

半拉格朗日法

把每个单元格中心视为一个粒子，沿着速度场回溯，在dt时刻之前位于哪个位置的粒子在会运动到当前的位置（s = so + v*dt, so = s - v*dt），线性插值出dt时间粒子，将此粒子视为当期时刻的粒子。

第四项对应论文中的投射项（Project），主要求解压力p，由于流体的分子可以相互移动，它们往往会“挤压”和“晃动”。当力施加到流体上时，它不会立即传播到整个体积。相反，靠近力的分子推到更远的分子上，压力就会增加。因为压力是单位面积的力，所以流体中的任何压力都会自然地导致加速度。这里作者在论文中拆分为三步去求解p：

第一步，求负的散度场，负的意义在解泊松方程，可以少一次乘以-1的操作：

-div = -0.5*(ui + 1 – ui - 1 + vi + 1 – vi - 1 + wi + 1 – wi - 1)/dx

第二步，这里使用到了亥姆霍兹-霍奇分解定理，即任何一个向量场都可以分解为一个无散向量场和梯度标量场。也就是求出什么场p的二阶导会造成这个散度场？这里用到了和之前求解扩散项相似的迭代法去求解。

《小时百科：亥姆霍兹分解》

第三步，解出了p，我们再减去p的梯度场，求出速度，就满足了所谓投射，也是确保了稳定性。

u -=(p[i+1,,]-p[i-1,,])/2dx
v -=(p[,j+1,]-p[,j-1,])/2dx

二、实现过程

在UE中实现GPU流体模拟的方式有很多，例如比较出名的FluidNinja流体插件是通过在动态材质实例中计算输出到RT中实现的，本文主要在Niagara中GPU模拟阶段实现该过程。

1. 基础搭建

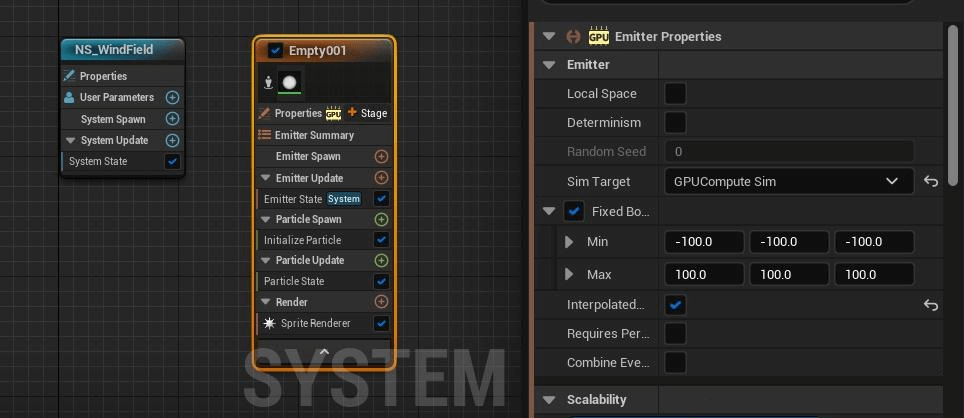
创建一个空发射器，Sim Target改成GPUCompute Sim，然后Fixed Bounds。

在User Exposed中，创建一个Texture Render Target类型的变量，命名为WindFieldRT，作为输出调试的RT。创建一个int类型的变量，命名为resolution，作为到Render Target的分辨率。

在Emitter Attribute中，创建一个Grid3D Collection类型的变量，命名为VelocityGrid，设置Num Attribute为3。创建一个Render Target 2D类型的变量，命名为RT_WindField，设置Over Render Target Format为RGBA 16f，Render Target User Parameter为刚刚创建的WindFieldRT。

创建一个Niagara Module Script，命名为NMS_SetResolution，用于设置VelocityGrid的网格数以及RT_WindField分辨率。注意这里我们需要将3D的Grid写入到2D的RT中，采用Z轴切片然后平铺到Y轴的方式。所以Render Target分辨率为（x,y*z）。

创建一个Niagara Module Script，命名为NMS_ExportToRT，用于将Grid3D的信息写入到RT中。这个时候可以试下修改一下Grid3D中的值，如果RT也跟着变化，证明从Grid3D写入到RT成功。

注意接下来每一项的计算都需要在独立的Simulation Stages中进行，因为放在同一个Stages下可视为同时并行计算，输入的Grid为上一帧的计算结果。

创建一张Render Target，命名为RT_WindField。创建一个Actor蓝图，添加Niagara组件，将参数WindFieldRT设置为刚刚创建的RT_WindField，分辨率为128。将蓝图拖入到场景中。

2. AddSource（外力项）
这里的外力只考虑碰撞产生的作用力，这是外界影响流体的主要来源。要获取某一位置是否与角色发生碰撞需要先从Grid3D中的索引位置还原到世界位置。

其中输入项Grid为VelocityGrid，Size为自定义的风场模拟范围，WorldPosition为风场组件所在的世界位置。计算出每个单元格所在的世界位置。

cellWorldPosition = (float3(x,y,z) / res) * size + worldPosition;

新增输入项PhysicsAsset为碰撞检测源，dt为单位时间，这里我使用Engine Provided的DeltaTime。

通过输入cellWorldPosition到Get Closest Element节点获取到该位置点与PhysicsAsset的最近距离（Closest Distance）与最近位置点的速度（Closest Velocity）。这里需要做一次判断，当位置点PhysicsAsset内部时，Closest Distance的值为负数，我们只需要与PhysicsAsset相交部分的位置点的速度，其他位置速度则无意义。将该速度作为速度源最后与上一帧的速度叠加。

视频

3. Diffuse（扩散项）

float a= dt * diff * N * N * N;

float VX_self;
Grid.GetGridValue(IndexX,IndexY,IndexZ,VectorIndex, VX_self);
float VX_right;
Grid.GetGridValue(IndexX+1,IndexY,IndexZ,VectorIndex, VX_right);
float VX_left;
Grid.GetGridValue(IndexX-1,IndexY,IndexZ,VectorIndex, VX_left);
float VX_up;
Grid.GetGridValue(IndexX,IndexY+1,IndexZ,VectorIndex, VX_up);
float VX_down;
Grid.GetGridValue(IndexX,IndexY-1,IndexZ,VectorIndex, VX_down);
float VX_front;
Grid.GetGridValue(IndexX,IndexY,IndexZ+1,VectorIndex, VX_front);
float VX_back;
Grid.GetGridValue(IndexX,IndexY,IndexZ-1,VectorIndex, VX_back);

float VY_self;
Grid.GetGridValue(IndexX,IndexY,IndexZ,VectorIndex+1, VY_self);
float VY_right;
Grid.GetGridValue(IndexX+1,IndexY,IndexZ,VectorIndex+1, VY_right);
float VY_left;
Grid.GetGridValue(IndexX-1,IndexY,IndexZ,VectorIndex+1, VY_left);
float VY_up;
Grid.GetGridValue(IndexX,IndexY+1,IndexZ,VectorIndex+1, VY_up);
float VY_down;
Grid.GetGridValue(IndexX,IndexY-1,IndexZ,VectorIndex+1, VY_down);
float VY_front;
Grid.GetGridValue(IndexX,IndexY,IndexZ+1,VectorIndex+1, VY_front);
float VY_back;
Grid.GetGridValue(IndexX,IndexY,IndexZ-1,VectorIndex+1, VY_back);

float VZ_self;
Grid.GetGridValue(IndexX,IndexY,IndexZ,VectorIndex+2, VZ_self);
float VZ_right;
Grid.GetGridValue(IndexX+1,IndexY,IndexZ,VectorIndex+2, VZ_right);
float VZ_left;
Grid.GetGridValue(IndexX-1,IndexY,IndexZ,VectorIndex+2, VZ_left);
float VZ_up;
Grid.GetGridValue(IndexX,IndexY+1,IndexZ,VectorIndex+2, VZ_up);
float VZ_down;
Grid.GetGridValue(IndexX,IndexY-1,IndexZ,VectorIndex+2, VZ_down);
float VZ_front;
Grid.GetGridValue(IndexX,IndexY,IndexZ+1,VectorIndex+2, VZ_front);
float VZ_back;
Grid.GetGridValue(IndexX,IndexY,IndexZ-1,VectorIndex+2, VZ_back);

float3V_self= float3(VX_self,VY_self,VZ_self);
float3V_right= float3(VX_right,VY_right,VZ_right);
float3V_left= float3(VX_left,VY_left,VZ_left);
float3V_up= float3(VX_up,VY_up,VZ_up);
float3V_down= float3(VX_down,VY_down,VZ_down);
float3V_front= float3(VX_front,VY_front,VZ_front);
float3V_back= float3(VX_back,VY_back,VZ_back);

diffusion =(V_self + a *(V_right + V_left + V_up + V_down + V_front + V_back))/(1+6* a);

采样上文推导出的x = (x0 + a*sum_c*dt)/(1 + a*num*dt) 进行迭代（迭代次数在10次以上更佳），其中输入的diff 为扩散系数，可以在外部输入，值越大则单元格之间交换速度越大，效果上表现为流体越稀反之则越稠。

视频

4. Advect（平流项）

float dt0= dt * N;
floati=IndexX;
floatj=IndexY;
floatk=IndexZ;

float U;
Grid.GetGridValue(IndexX,IndexY,IndexZ,VectorIndex, U);
float V;
Grid.GetGridValue(IndexX,IndexY,IndexZ,VectorIndex+1, V);
float W;
Grid.GetGridValue(IndexX,IndexY,IndexZ,VectorIndex+2, W);

floatx= i - dt0 * U;
floaty= j - dt0 * V;
floatz= k - dt0 * W;

x = clamp( x,0.5, N +0.5);
y = clamp( y,0.5, N +0.5);
z = clamp( z,0.5, N +0.5);

intx0=int(x);
inty0=int(y);
intz0=int(z);

floatx1= x0 +1;
floaty1= y0 +1;
floatz1= z0 +1;

floatxd=(x - x0)/(x1 - x0);
floatyd=(y - y0)/(y1 - y0);
floatzd=(z - z0)/(z1 - z0);

float VX000;
Grid.GetGridValue(x0, y0, z0,VectorIndex, VX000);
float VX100;
Grid.GetGridValue(x1, y0, z0,VectorIndex, VX100);
float VX010;
Grid.GetGridValue(x0, y1, z0,VectorIndex, VX010);
float VX001;
Grid.GetGridValue(x0, y0, z1,VectorIndex, VX001);
float VX101;
Grid.GetGridValue(x1, y0, z1,VectorIndex, VX101);
float VX011;
Grid.GetGridValue(x0, y1, z1,VectorIndex, VX011);
float VX110;
Grid.GetGridValue(x1, y1, z0,VectorIndex, VX110);
float VX111;
Grid.GetGridValue(x1, y1, z1,VectorIndex, VX111);

float VY000;
Grid.GetGridValue(x0, y0, z0,VectorIndex+1, VY000);
float VY100;
Grid.GetGridValue(x1, y0, z0,VectorIndex+1, VY100);
float VY010;
Grid.GetGridValue(x0, y1, z0,VectorIndex+1, VY010);
float VY001;
Grid.GetGridValue(x0, y0, z1,VectorIndex+1, VY001);
float VY101;
Grid.GetGridValue(x1, y0, z1,VectorIndex+1, VY101);
float VY011;
Grid.GetGridValue(x0, y1, z1,VectorIndex+1, VY011);
float VY110;
Grid.GetGridValue(x1, y1, z0,VectorIndex+1, VY110);
float VY111;
Grid.GetGridValue(x1, y1, z1,VectorIndex+1, VY111);

float VZ000;
Grid.GetGridValue(x0, y0, z0,VectorIndex+2, VZ000);
float VZ100;
Grid.GetGridValue(x1, y0, z0,VectorIndex+2, VZ100);
float VZ010;
Grid.GetGridValue(x0, y1, z0,VectorIndex+2, VZ010);
float VZ001;
Grid.GetGridValue(x0, y0, z1,VectorIndex+2, VZ001);
float VZ101;
Grid.GetGridValue(x1, y0, z1,VectorIndex+2, VZ101);
float VZ011;
Grid.GetGridValue(x0, y1, z1,VectorIndex+2, VZ011);
float VZ110;
Grid.GetGridValue(x1, y1, z0,VectorIndex+2, VZ110);
float VZ111;
Grid.GetGridValue(x1, y1, z1,VectorIndex+2, VZ111);

float3V000= float3(VX000,VY000,VZ000);
float3V100= float3(VX100,VY100,VZ100);
float3V010= float3(VX010,VY010,VZ010);
float3V001= float3(VX001,VY001,VZ001);
float3V101= float3(VX101,VY101,VZ101);
float3V011= float3(VX011,VY011,VZ011);
float3V110= float3(VX110,VY110,VZ110);
float3V111= float3(VX111,VY111,VZ111);

//三线性差值
Advect= V000 *(1- xd)*(1- yd)*(1- zd)+
V100 * xd *(1- yd)*(1- zd)+
V010 *(1- xd)* yd *(1- zd)+
V001 *(1- xd)*(1- yd)* zd +
V101 * xd *(1- yd)* zd +
V011 *(1- xd)* yd * zd +
V110 * xd * yd *(1- zd)+
V111 * xd * yd * zd;

如图所示（每个小格边长为0.25），当前帧单元格（黄色点位置）的速度为(2.75,1.25)，通过回溯上一帧位置（蓝色点），采样该点相邻的单元格的值进行线性差值，得到结果作为下一帧的速度，这一步主要是半拉格朗日法的实现。

视频

5. Project（投射项）

分别创建两张Grid2D，命名为DivergenceGrid和PressureGrid，用于计算散度和压力梯度。这里我们分成三步Simulation Stage去分别计算当前速度场的散度场，根据亥姆霍兹分解定理通过迭代的方式求出该速度场的梯度场，以及梯度场相减得到速度场。

计算散度

计算梯度压力

梯度相减得到速度

视频

6. 边界问题
经过四项计算后我们可以得到较为真实的流体模拟效果，但是我们的模拟只能在模拟框范围内计算，当角色超出边界时则不再有新的外力进来。

视频

这种问题最简单的解决方式是构建一个跟场景大小匹配的模拟框，以确保角色不会超出边界，但这样我们就需要定义一张包含整张地图的Grid，但我们需要的效果只是角色周围的一小范围内，这样显然不划算。

既然我们只需要距离角色一定范围内才有交互风的效果，参考《战神》中风场的做法，我们可以让风场模拟框跟随角色移动，风场信息在Grid上每一帧往角色运动反方向做偏移，这样只需要很小的固定消耗就能实现全地图的交互风场效果。

float x=IndexX+Veloctiy.x;
floaty=IndexY+Veloctiy.y;
floatz=IndexZ+Veloctiy.z;

intx0=int(x);
inty0=int(y);
intz0=int(z);

floatx1= x0 +1;
floaty1= y0 +1;
floatz1= z0 +1;

floatxd=(x - x0)/(x1 - x0);
floatyd=(y - y0)/(y1 - y0);
floatzd=(z - z0)/(z1 - z0);

float VX000;
Grid.GetGridValue(x0, y0, z0,VectorIndex, VX000);
float VX100;
Grid.GetGridValue(x1, y0, z0,VectorIndex, VX100);
float VX010;
Grid.GetGridValue(x0, y1, z0,VectorIndex, VX010);
float VX001;
Grid.GetGridValue(x0, y0, z1,VectorIndex, VX001);
float VX101;
Grid.GetGridValue(x1, y0, z1,VectorIndex, VX101);
float VX011;
Grid.GetGridValue(x0, y1, z1,VectorIndex, VX011);
float VX110;
Grid.GetGridValue(x1, y1, z0,VectorIndex, VX110);
float VX111;
Grid.GetGridValue(x1, y1, z1,VectorIndex, VX111);

float VY000;
Grid.GetGridValue(x0, y0, z0,VectorIndex+1, VY000);
float VY100;
Grid.GetGridValue(x1, y0, z0,VectorIndex+1, VY100);
float VY010;
Grid.GetGridValue(x0, y1, z0,VectorIndex+1, VY010);
float VY001;
Grid.GetGridValue(x0, y0, z1,VectorIndex+1, VY001);
float VY101;
Grid.GetGridValue(x1, y0, z1,VectorIndex+1, VY101);
float VY011;
Grid.GetGridValue(x0, y1, z1,VectorIndex+1, VY011);
float VY110;
Grid.GetGridValue(x1, y1, z0,VectorIndex+1, VY110);
float VY111;
Grid.GetGridValue(x1, y1, z1,VectorIndex+1, VY111);

float VZ000;
Grid.GetGridValue(x0, y0, z0,VectorIndex+2, VZ000);
float VZ100;
Grid.GetGridValue(x1, y0, z0,VectorIndex+2, VZ100);
float VZ010;
Grid.GetGridValue(x0, y1, z0,VectorIndex+2, VZ010);
float VZ001;
Grid.GetGridValue(x0, y0, z1,VectorIndex+2, VZ001);
float VZ101;
Grid.GetGridValue(x1, y0, z1,VectorIndex+2, VZ101);
float VZ011;
Grid.GetGridValue(x0, y1, z1,VectorIndex+2, VZ011);
float VZ110;
Grid.GetGridValue(x1, y1, z0,VectorIndex+2, VZ110);
float VZ111;
Grid.GetGridValue(x1, y1, z1,VectorIndex+2, VZ111);

float3V000= float3(VX000,VY000,VZ000);
float3V100= float3(VX100,VY100,VZ100);
float3V010= float3(VX010,VY010,VZ010);
float3V001= float3(VX001,VY001,VZ001);
float3V101= float3(VX101,VY101,VZ101);
float3V011= float3(VX011,VY011,VZ011);
float3V110= float3(VX110,VY110,VZ110);
float3V111= float3(VX111,VY111,VZ111);

//三线性差值
value = V000 *(1- xd)*(1- yd)*(1- zd)+
V100 * xd *(1- yd)*(1- zd)+
V010 *(1- xd)* yd *(1- zd)+
V001 *(1- xd)*(1- yd)* zd +
V101 * xd *(1- yd)* zd +
V011 *(1- xd)* yd * zd +
V110 * xd * yd *(1- zd)+
V111 * xd * yd * zd;

还需要在蓝图中实时设置位置为角色位置，并设置WorldPosition（角色世界位置）、LastFramePosition（上一帧位置，用于计算移动偏移）、FieldSize（模拟框大小），三个参数实时更新到Niagara。在Niagara中根据当前位置跟上一帧位置的插值对风场进行相对偏移。

这一步其实跟求平流项的半拉格朗日法很像，只不过速度用的是相对整体偏移的速度。

这样我们就得到一个跟随角色移动的模拟框，并且计算消耗控制在模拟框范围内，超出则不参与计算。

视频

7. 采样风场

再定义一张1x3大小的RT命名为RT_Data，这里RT初始化等操作与上述RT_WindField一致，可以参RT_WindField的设置，然后将风场组件位置（上述步骤中从蓝图传入的WorldPosition）、风场模拟框大小（FieldSize）以及分辨率分别写入到三个像素中，RT_Data可以理解成自定义的一种结构体，用于后续在其他粒子系统中采样风场提供实时更新的参数。

有了RT_Data的写入，接下来就是读取，这里我定义了一个Niagara Function Script，命名为NFS_ParseWindFieldData，在里面只需要读取该RT三个像素每个像素中心点的值即可解析得到位置、大小和分辨率三个值。

创建一个Niagara Module Script，命名为NMS_WindForce，用于在其他粒子系统中采样风场RT的值作为外力来驱动粒子运动。在新的Niagara中创建一个Fountain粒子发射器，拖入NMS_WindForce模块，设置RT_Data、RT_WindField和分辨率。