如何在UE4中做出涟漪的效果
涟漪这个效果我相信很多人都尝试实现过,也有各种实现方法。在这里,我实现的方法是使用Custom节点,用算法生成法线。接下来向大家分享一下思路,看一下最终效果图。文末提供了材质球百度云链接。

最终效果图
简单地说一下原理:先用UV做出伪随机的格子,每个格子就是一个单独的UV,不过具有不同的灰度值,然后在格子的中心生成多个不同大小的同心圆,再做缩放和边缘混合。
随机噪波生成
首先,我们先定义一个三维向量用来进行三层不同大小涟漪的计算,因为UV的取值范围是0-1,所以我们定义的float3的值必须在0-1之间。这个值是一个系数,并不是实际的大小:
float3 ripple_scale3=float3(0.1,0.2,0.3)
然后,我们需要生成带有不同的灰度的UV格子:
float3 p3 = frac(float3(p.xyx) * ripple_scale3); p3 += dot(p3, p3.yzx +20); return frac((p3.xy + p3.yz) * p3.zy);
p是一个二维的向量,为了能和ripple_scale相乘,所以我们可以随便取它的.XYX或者.XYY。p3则是一个累加值,最后返回的值则是一个float2,因为UV是float2,随便取两个轴进行上述的运算就可以。然后我们定义一个一维的向量再次进行如下运算:
float ripple_scale1 = 0.1; float3 p3 = frac(float3(p.xyx) * ripple_scale1); p3 += dot(p3, p3.yzx + 10); return frac((p3.x + p3.y) * p3.z);
上述的两个运算主要是为了得出一个足够随机的值,也可以用其它算法替代。我们如果将UV tiling 10次,然后floor之后作为上面代码中p的值,先进行三维的运算然后和下面一维的相乘可以得到如下结果(只要得到类似如下结果的算法都可以):
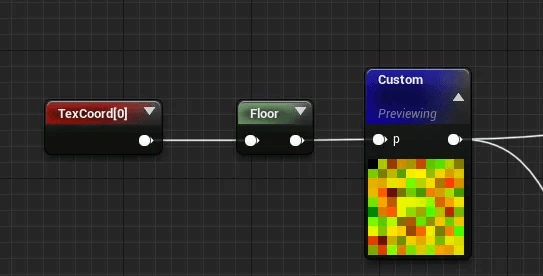
这个算法我们需要将其作为一个function,因为需要循环计算,所以得用一个strcut结构体进行声明后调用。
float ripple_scale1 = 0.1;一维随机数种子
float3 ripple_scale3 = float3(0.1, 0.11, 0.09);//三维随机数种子
float max_radius = 1;
struct rain
{
float ripple1(float2 p)
{
float3 p3 = frac(float3(p.xyx) * ripple_scale1);
p3 += dot(p3, p3.yzx + 10);
return frac((p3.x + p3.y) * p3.z);
}
float2 ripple2(float2 p)
{
float3 p3 = frac(float3(p.xyx) * ripple_scale3);
p3 += dot(p3, p3.yzx +20);
return frac((p3.xy + p3.yz) * p3.zy);
}
};
rain ra;
涟漪形状生成
接下来就是通过随机值产生涟漪并且动起来,这步需要循环采样,先把需要用到的变量声明一下:
float tiling = 10;//UVtiling次数 float2 uv = (UV) * tiling;//UV float2 p0 = floor(uv);//floor之后会产生tiling个数长宽的UV格子 float i = 0;//x轴循环次数 float j = 0;//y轴循环次数,因为UV是双轴的所以有两个方向 float2 pi = 0;记录每个UV格子的不同灰度 float2 circles = 0;//圆圈 float2 p = 0;//初始位置
再准备循环体,把pi放入循环体进行累加:
for (j = (- max_radius);j <= max_radius; j++)
for (i = - max_radius; i<= max_radius; i++)
{
pi = p0 +float2(i, j);
}
}
由于上述累加结果过大,我们将其进行除以tiling次数方便观察,很明显每个格子已经有了不一样的灰度值,因为i、j的值一直在累加。

pi循环后的值
然后我们在pi下面将pi的值代入三维的随机数function里进行运算:
for (j = (- max_radius);j <= max_radius; j++)
{
for (i = - max_radius; i<= max_radius; i++)
{
pi = p0 +float2(i, j);
float2 hsh = ra.ripple2(pi);//第一次随机运算
}
}

hsh循环后的值(随机化)
有了第一次就有第二次,我们继续将hsh的值再代入三维的随机值进行二次随机化,然后和pi的值加起来就能得到带有pi(UV位置信息的随机值),也就是我们的p。
for (j = (- max_radius);j <= max_radius; j++)
{
{
pi = p0 +float2(i, j);
float2 hsh = ra.ripple2(pi);//第一次随机运算
p = pi + ra.ripple2(hsh);//得到带位置信息的随机值
}
}

p的值,同样便于观察除以了tiling值
然后,我们需要定义一个时间值t,同样需要随机化,但是是用一维的随机化函数(如果继续用三维会产生tiling,参考下图(下图中的tiling值为20)),然后frac做0-1循环。
for (j = (- max_radius);j <= max_radius; j++)
{
for (i = - max_radius; i<= max_radius; i++)
{
pi = p0 +float2(i, j);
float2 hsh = ra.ripple2(pi);//第一次随机运算
p = pi + ra.ripple2(hsh);//得到带位置信息的随机值
float t = frac(0.3 * iTime + ra.ripple1(hsh));//随机时间产生,0.3为速度,可在外部调整
}
}
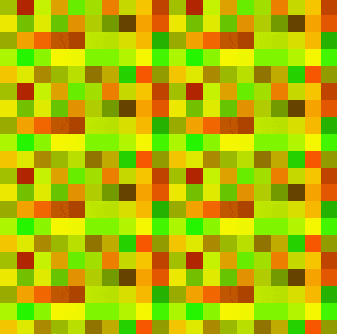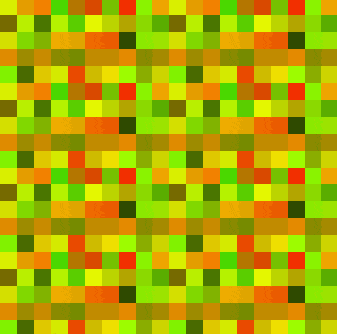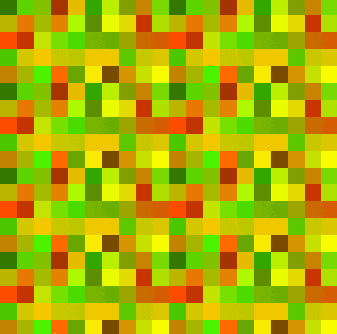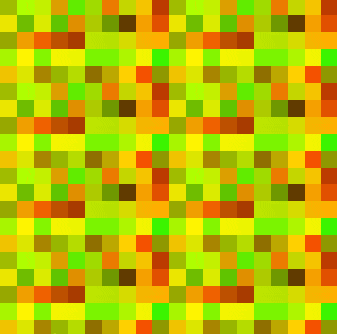
只采用一种随机化的t

采用两种随机化的t
然后我们需要得出实际的位置,我这边用v表示,只需要减去UV值就行了,因为需要和UV对应起来。如果不减,我们最后将得不到法线(平的):
for (j = (- max_radius);j <= max_radius; j++)
{
for (i = - max_radius; i<= max_radius; i++)
{
pi = p0 +float2(i, j);
float2 hsh = ra.ripple2(pi);//第一次随机运算
p = pi + ra.ripple2(hsh);//得到带位置信息的随机值
float t = frac(0.3 * iTime + ra.ripple1(hsh));//随机时间产生,0.3为速度,可在外部调整
float2 v = p - uv;//实际位置信息
}
}
接下来就是计算圆了。圆的计算公式是length(position)-R,其中position是圆心在UV中的位置,R是圆的半径。我们这边是max_radius+1,如果不加1,所有值都会比原来的小,这样会导致法线强度太弱,然后乘以我们得到的t就可以产生扩散的圆了:
for (j = (- max_radius);j <= max_radius; j++)
{
for (i = - max_radius; i<= max_radius; i++)
{
pi = p0 +float2(i, j);
float2 hsh = ra.ripple2(pi);//第一次随机运算
p = pi + ra.ripple2(hsh);//得到带位置信息的随机值
float t = frac(0.3 * iTime + ra.ripple1(hsh));//随机时间产生,0.3为速度,可在外部调整
float2 v = p - uv;//实际位置信息
float d = length(v) - (max_radius + 1) * t;//计算圆
}
}

计算出来的扩散圆
但是因为这个只是其中一部分,圆形状的累加我们等会再做,先把涟漪的形状做出来。其实很简单,将得到的d进行sine函数运算一下就能得到涟漪,将d和一个值相乘能得到不同圈数的涟漪,然后用smoothstep控制涟漪的边缘虚实效果。我们这边要做两层,用两层的插值来模拟渐变,用h来控制涟漪的偏移值。
for (j = (- max_radius);j <= max_radius; j++)
{
for (i = - max_radius; i<= max_radius; i++)
{
pi = p0 +float2(i, j);
float2 hsh = ra.ripple2(pi);//第一次随机运算
p = pi + ra.ripple2(hsh);//得到带位置信息的随机值
float t = frac(0.3 * iTime + ra.ripple1(hsh));//随机时间产生,0.3为速度,可在外部调整
float2 v = p - uv;//实际位置信息
float d = length(v) - (max_radius + 1) * t;//计算圆
float h = 1e-3;//就是0.001
float d1 = d - h;
float d2 = d + h;
float p1 = sin(31. * d1) * smoothstep(-0.6, -0.3, d1) * smoothstep(0., -0.3, d1);
float p2 = sin(31. * d2) * smoothstep(-0.6, -0.3, d2) * smoothstep(0., -0.3, d2);
}
}

d*30

d*60

p1的效果
涟漪渐变效果
能动起来后,我们需要一个到达最大值后渐隐的效果,通过两者的差值乘以时间的反向,即1-0来模拟边缘的渐变效果,乘以两次时间是为了增强对比度。
for (j = (- max_radius);j <= max_radius; j++)
{
for (i = - max_radius; i<= max_radius; i++)
{
pi = p0 +float2(i, j);
float2 hsh = ra.ripple2(pi);//第一次随机运算
p = pi + ra.ripple2(hsh);//得到带位置信息的随机值
float t = frac(0.3 * iTime + ra.ripple1(hsh));//随机时间产生,0.3为速度,可在外部调整
float2 v = p - uv;//实际位置信息
float d = length(v) - (max_radius + 1) * t;//计算圆
float h = 1e-3;//就是0.001
float d1 = d - h;
float d2 = d + h;
float p1 = sin(31. * d1) * smoothstep(-0.6, -0.3, d1) * smoothstep(0., -0.3, d1);
float p2 = sin(31. * d2) * smoothstep(-0.6, -0.3, d2) * smoothstep(0., -0.3, d2);
circles = (p2 - p1) / (2. * h) * (1. - t) * (1. - t);//渐隐效果
}
}

达到最大值后渐隐效果
涟漪形状累加
然后我们乘以它原来的normalize后的position(即v),即可得到现在的正确的法线效果,最后将每次循环的结果累加起来就可以得到我们想要的涟漪,再乘以数值可以控制法线强度:
for (j = (- max_radius);j <= max_radius; j++)
{
for (i = - max_radius; i<= max_radius; i++)
{
pi = p0 +float2(i, j);
float2 hsh = ra.ripple2(pi);//第一次随机运算
p = pi + ra.ripple2(hsh);//得到带位置信息的随机值
float t = frac(0.3 * iTime + ra.ripple1(hsh));//随机时间产生,0.3为速度,可在外部调整
float2 v = p - uv;//实际位置信息
float d = length(v) - (max_radius + 1) * t;//计算圆
float h = 1e-3;//就是0.001
float d1 = d - h;
float d2 = d + h;
float p1 = sin(31. * d1) * smoothstep(-0.6, -0.3, d1) * smoothstep(0., -0.3, d1);
float p2 = sin(31. * d2) * smoothstep(-0.6, -0.3, d2) * smoothstep(0., -0.3, d2);
circles = (p2 - p1) / (2. * h) * (1. - t) * (1. - t);//渐隐效果
circles = 0.5 * normalize(v) * ((p2 - p1) / (2. * h) * (1. - t) * (1. - t));//得到正确法线方向
circles=circles+circles;//效果累加
}
}

circles法线累加效果
有了这个,我们法线的形状对了,但是效果不美观。因为是累加起来的,所以循环结束后除以循环总次数,即可得到正确的效果:
circles /= float(max_radius*2+1)*(max_radius*2+1);

颜色矫正后的效果
生成法线
最后用求法线B通道的方式(开平方)求出B通道输出即可,为什么用点积做平方,我想大家都懂:
float3 n = float3(circles, sqrt(1. - dot(circles, circles)));

法线效果
下面是完整代码:
float3 ripple_scale= float3(0.1,0.2,0.3);
float max_radius = 2;
struct rain
{
float2 ripple(float2 p)
{
float3 p3 = frac(float3(p.xyx) * ripple_scale);
p3 +=p3;
return frac((p3.xy + p3.yz) * p3.zy);
}
};
rain ra;
float tiling = 10;
float2 uv = (UV) * tiling;
float2 p0 = floor(uv);
float j = 0;
float i = 0;
float2 pi = 0;
float2 circles = 0;
float2 p = 0;
for (j = (- max_radius);j <= max_radius; j++)
{
for (i = - max_radius; i<= max_radius; i++)
{
pi = p0 +float2(j, i);
p = pi+ra.ripple(pi);
float t = frac(iTime + ra.ripple(pi));
float2 v = p - uv;
float d = length(v) - (max_radius + 1) * t;
float h = 0.01;
float d1 = d - h;
float d2 = d + h;
float p1 = sin(30 * d1) * smoothstep(-0.6, -0.3, d1) * smoothstep(0., -0.3, d1);
float p2 = sin(30. * d2) * smoothstep(-0.6, -0.3, d2) * smoothstep(0., -0.3, d2);
circles += 0.5 * normalize(v)* ((p2-p1 )/(2. * h) * (1. - t) * (1. - t)) ;
}
}
circles /= pow((max_radius*2+1),2);
float3 n = float3(circles, sqrt(1. - dot(circles, circles)));
return n;
水底石头生成
石头部分直接用Parallax就可以了,如果看过我前面文章的朋友可以用我前面改过的算法:
《如何在UE4中用raymarch实现面片水体(采样贴图)》
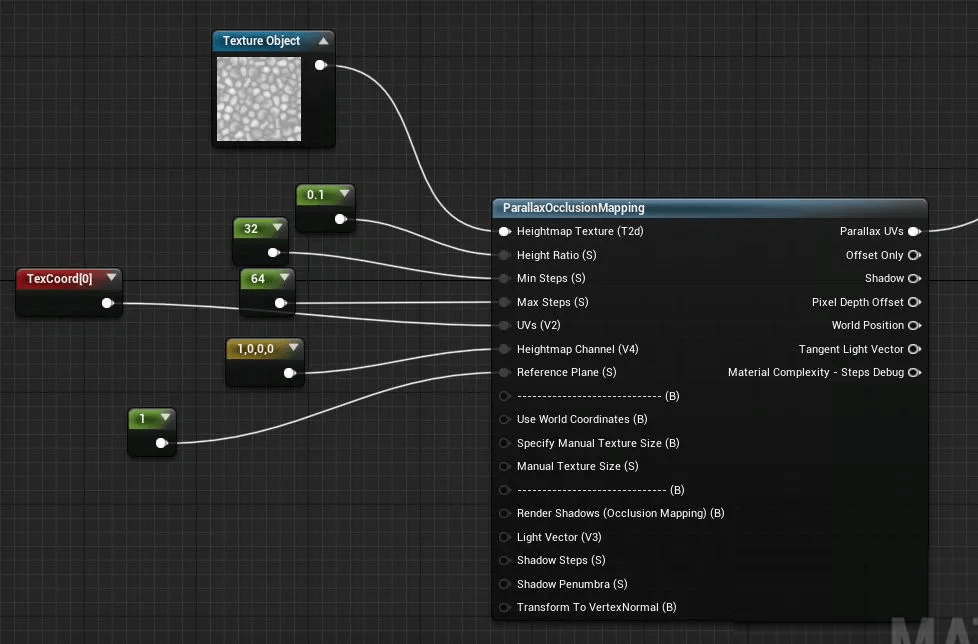
POM石头的高度图
反射
水面反射依旧使用Reflection Vector,我们最后的法线就是输入到这个normal接口,我这边用另一张法线和上面的ripple做了min让圆圈稍微产生了些变化:
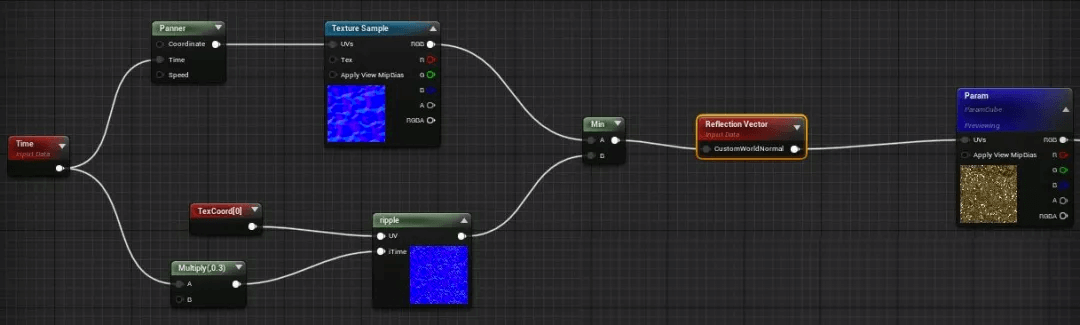

输出到Reflection Vector的结果
折射
对于折射,我这边是将上面的法线混合结果直接加到石头颜色的UV上就可以模拟了,当然强度得小一些。
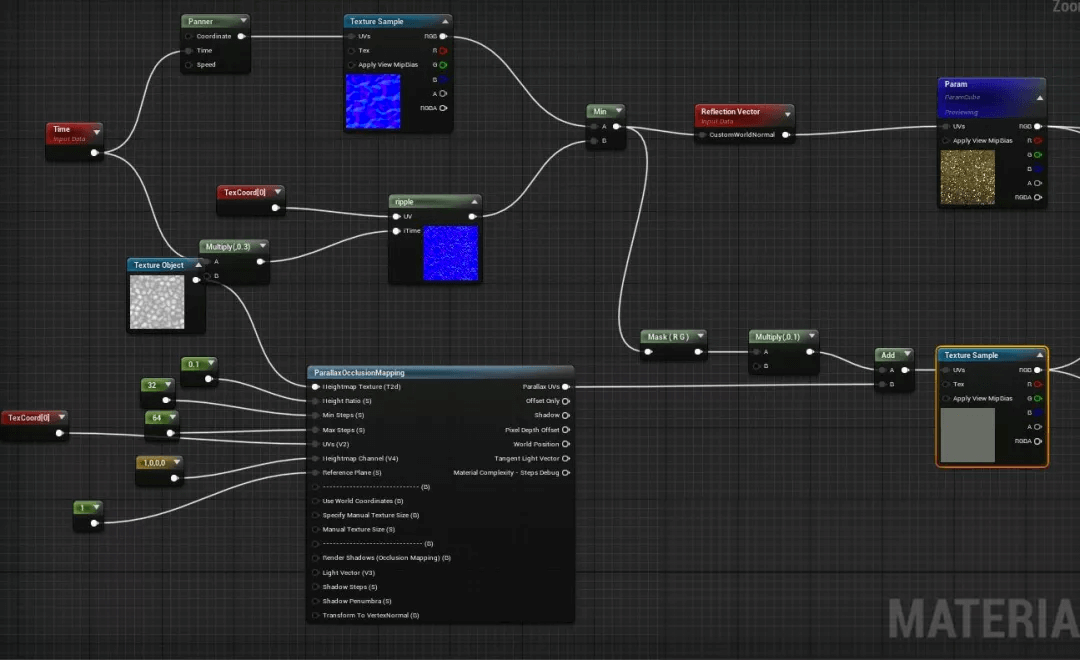
折射和反射
透明度
最后用菲涅尔做出深度和透明度的变化就可以了:
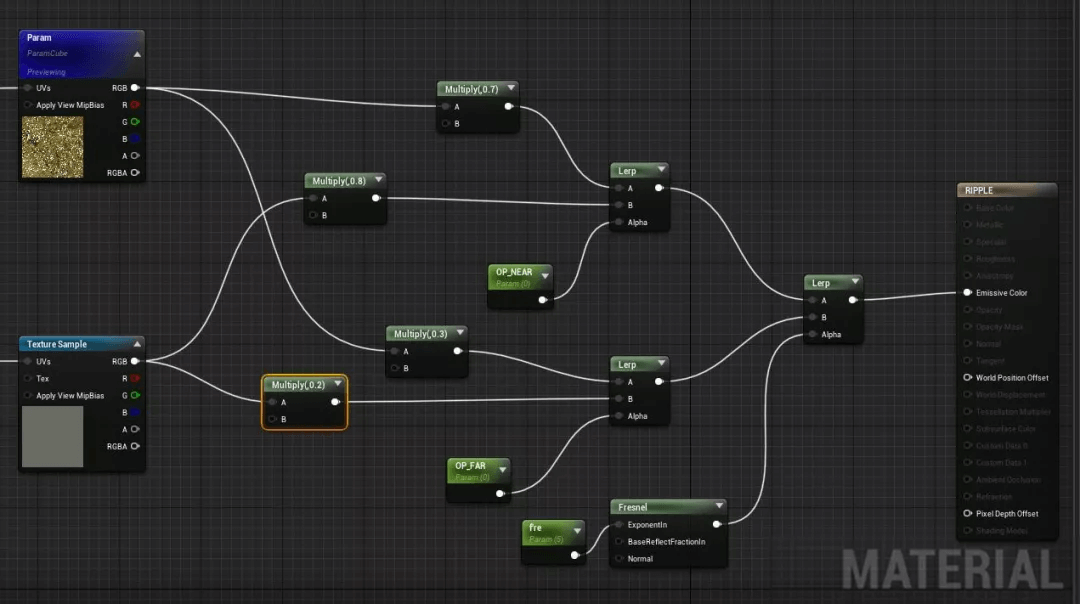
菲涅尔制作深度和透明度
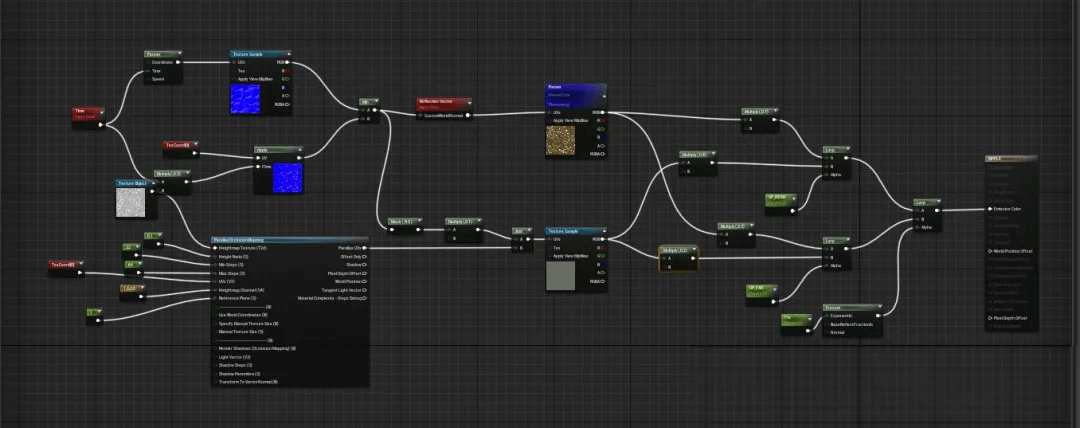
完整节点
材质球的百度云链接:
链接:https://pan.baidu.com/s/1xXvxxsYBjBVVnb42wOWFrA
提取码:fp37
这是侑虎科技第1021篇文章,感谢作者落月满江树供稿。欢迎转发分享,未经作者授权请勿转载。如果您有任何独到的见解或者发现也欢迎联系我们,一起探讨。(QQ群:793972859)
作者主页:https://www.zhihu.com/people/luo-yue-man-jiang-shu-38,再次感谢落月满江树的分享,如果您有任何独到的见解或者发现也欢迎联系我们,一起探讨。(QQ群:793972859)





