决策树的一些定义和公式

信息熵：在特定单位内携带的信息量。熵越大：表示越混乱，信息越多，越难理解。熵越小：表示越有序，信息越少，轻松理解。熵为0时，表示稳定不变

http://baike.baidu.com/link?url=4HpUnEU3GBoOEv1nbE1DzLh8xGDuDiMv_S5F7W6Bua0xgB3GZMihL-Q3tRs7romcJBENwIXs7E44Bg6wUhMkHFhjSSe2QR3BaqTOsseDpzQPOj2Pe0Bq7Uu8J6m422tz

如有错误请指正

以下所有公式中都是以2为底

公式：H(X)=–∑P(x)log[P(x)]

　　H(x)：表示熵

　　P(x)：表示x事件发生的概率

推导过程：我没有找到。。。

举例：

　　原文：http://www.cnblogs.com/leoo2sk/archive/2010/09/19/decision-tree.html

　　计算账号是否真实的信息熵：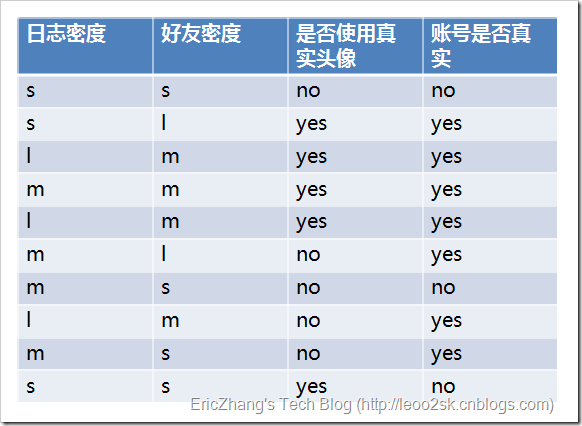

　　账号真实的概率：7/10=0.7

　　账号虚假的概率：3/10=0.3

　　带入公式

　　账号是否真实的信息熵：-(0.7log0.7+0.3log0.3)=-(0.7*-0.51+0.3*-1.74)=0.879

条件熵：x,y两个条件，在已知x条件下的概率，求y的条件熵

　　原文定义：http://blog.csdn.net/gxiaob/article/details/8492380

　　公式：H(X=x|Y)= ∑p(y|x)log{1/p(y,x)}

　　举例：

　　　　例子原文：http://www.zybang.com/question/0297d53381c646ea0e8cfe46a4ecca75.html

　　　　//例子不对，注释掉下面的，直接看连接

　　　　//已知用户是否使用真实头像x，求用户是否真实的熵H(Y|X=x)

　　　　//用户使用头像的概率：P(用户头像)=10/10=1

　　　　//用户头像真实的概率：P(yes|用户头像)=1/2=0.5

　　　　//用户头像虚假的概率：p(no|用户头像)=1/2=0.5

　　　　论域U由14个气象状态组成，属性有五个，其中包含4个条件属性，分别为景象（outlook）、温度（temperature）、湿度（humidity）、刮风（windy）；一个决策属　　　　性（class），表示是否适合在室外打网球。决策属性值“y”表示“天气适合在室外打网球”，“n”表示“不适合在室外打网球”。

　　　　H(D|P)=-SIGMA(i)SIGMA(j)p(Pj)p(Di|Pj)log(p(Di|Pj))
　　　　=-[sunny+overcast+rain]
　　　　P=outlook
　　　　so P(sunny)=5/14
　　　　P(overcast)=4/14
　　　　P(rain)=5/14
　　　　P(y|sunny)=2/5
　　　　P(y|overcast)=1
　　　　P(y|rain)=3/5
　　　　P(n|sunny)=3/5
　　　　P(n|overcast)=0
　　　　P(n|rain)=2/5
　　　　所以
　　　　sunny=5/14 * (2/5 * log(2/5) + 1/5 * log(1/5))= -0.1044
　　　　overcast=4/14 * (0 + 1 * log(1))= -0
　　　　rain=5/14 * (2/5 * log(2/5) + 3/5 * log(3/5))= -0.1044
　　　　所以H(D|P)=-(-0.1044-0-0.1044)=0.2088
　　　　H(D|Q)=-SIGMA(i)SIGMA(j)p(Qj)p(Di|Qj)log(p(Di|Qj))
　　　　=-[hot+mild+cool]
　　　　P=outlook
　　　　所以Q(hot)=4/14
　　　　Q(mild)=6/14
　　　　Q(cool)=4/14
　　　　Q(y|hot)=2/4
　　　　Q(y|mild)=4/6
　　　　Q(y|cool)=3/4
　　　　Q(n|hot)=2/4
　　　　Q(n|mild)=2/6
　　　　Q(n|cool)=1/4
　　　　所以
　　　　hot=4/14 * (2/4 * log(2/4) + 2/4 * log(2/4))= -0.0860
　　　　mild=6/14 * (4/6 * log(4/6) + 2/6 * log(2/6))= -0.1185
　　　　cool=4/14 * (3/4 * log(3/4) + 1/4 * log(1/4))= -0.0698
　　　　so H(D|Q)=-(-0.0860-0.1185-0.0698)=0.2743

　　·　　

联合熵：指多个变量下，熵的变化

　　原文：http://blog.csdn.net/kxy_tech/article/details/3993457

　　　　http://www.zybang.com/question/906488ade9ebccc242dfc3fb527f60e3.html

　　公式H(X,Y)=-∑∑P(x,y)log[P(x,y)]

　　　　　　　=H(X)+H(Y|X)

　　　　　　　=H(Y)+H(X|Y)

　　例子：接上文，已知H(D|Q)=0.2743(由上题可得),求联合熵H(D,Q)

　　　　　H(Q)=0.301+0.2765+0.2443

　　　　　　　=0.8218

　　　　　H(D,Q)=H(Q)+H(D|Q)

　　　　　　　=0.8218+0.2743

　　　　　　　=1.0961

信息增益：假设有多个条件X,Y,Z。论X条件对最后导致的结果的重要程度

　　原文：https://www.zhihu.com/question/22104055

　　公式：信息增益=信息熵-条件熵

　　例子：接上文

　　　　已知条件熵H(D|Q)=0.2743(由上题可得),求信息增益

　　　　P(n|D)=5/14

　　　　P(y|D)=9/14

　　　　H(D)=-{5/14*log5/14+9/14log9/14}

　　　　信息增益=-(5/14*log5/14+9/14log9/14)-0.2743