给自己菜自闭了

是谁在给我点踩？👀

LOJ#3805. 「JOI Open 2022」长颈鹿

题意

称一个排列 \(q_1,q_2,\ldots,q_n\) 是合法的，当且仅当所有区间 \([l,r]\) 都不同时满足以下两个条件：

• 存在一个 \(k\in[l,r]\) 满足 \(q_k>q_l\) 且 \(q_k>q_r\)；
• 存在一个 \(k\in[l,r]\) 满足 \(q_k<q_l\) 且 \(q_k<q_r\)。

定义两个 \(n\) 阶排列 \(p,q\) 的不和谐度为 \(\sum\limits_{i=1}^n[p_i \neq q_i]\)，给出一个排列 \(p\)，求所有合法排列 \(q\) 与 \(p\) 的不和谐度的最小值。

\(n \leq 8000\)，排列 \(p\) 随机生成。7s/1G.

题解

先忽略掉 \(p\) 随机生成。

限制等价于对于任意一个区间，两端点之中必然存在区间最大/小值。如果把该数去掉，剩下的依然得是合法的，启示区间 DP。

状态不好直接设计，考虑合法序列 \(q\) 是如何被生成的。首先 \(q_1,q_n\) 中一定有一个是 \(1\) 或 \(n\)，把此数剔除并计算贡献，就这样每次剔除一个端点，我们发现没有填的数在值域上是连续的！这样就可以 \(dp_{l,r,x,y}\) 表示给 \(q[l,r]\) 填上 \([x,y]\) 的数后，这段区间的最小不和谐度。\(y\) 显然可以省掉，这样就 \(O(n^3)\) 了。

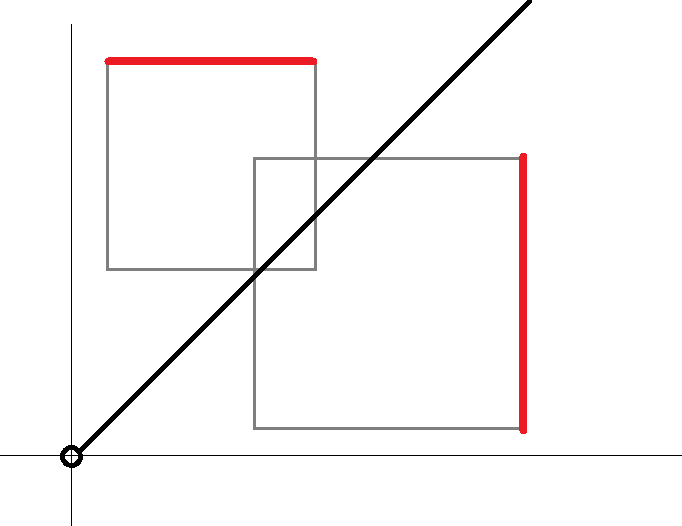
但显然无用状态太多了。如果我们统计相同位置的最大值（也就是长度减不和谐度）的话，我们发现 \(dp\) 值会变化的位置实际上非常少，很多状态无论 \(q_l,q_r\) 填 \(x,y\) 中的哪一个，都不等于 \(p_l,p_r\)。更直观地，我们把状态呈现在二维平面上，\(dp_{l,r,x,y}\) 代表一个横轴占据 \([l,r]\)，纵轴占据 \([x,y]\) 的正方形，\(p_i\) 为一个关键点 \((i,p_i)\)。每次转移相当于打掉正方形四个角中的一个，这个正方形的权值代表这个正方形内最多打掉多少个关键点（也就是DP 值），那么所谓有贡献的状态，就只能以关键点作为四角之一。

我们不妨考虑只在有用的状态间转移，也就是 \(dp_{l,r,0/1,0/1}\) 表示用一段值域连续的数填完了 \(q[l,r]\)，并且 \(p_{l/r}\) 作为最小/大值时，相同位置的最大数量。转移就变成了，找出被完全包含在其内的正方形的最大权值，利用数据结构优化转移，可以做到 \(O(n^2 \log^2 n)\)。

进而分析意义，一个正方形往被它包含的所有正方形连边，其权值即为最长路径。于是乎我们交换状态，记 \(dp_{k,l,0/1,0/1}\) 表示以 \((l,p_l)\) 作为左下/左上/右下/右上角时，正方形权值为 \(k\) 所需要的最短边长。

容易发现 \(dp_k\) 只会由 \(dp_{k-1}\) 转移来，那么分层转移，同一层的转移变成了：给定了一堆正方形，我要对每个点求出以其作为某个角时，至少包含一个正方形的最小边长。有一个 trick：查询时以对角线为分界线，对角线上/下的正方形只剩某一维有贡献，这样一次转移变成了 \(O(\log n)\)。

数据随机是什么寄吧啊？如果我只关注左上、右下角打掉的东西，这是 \(p\) 的一个递减子序列，也就是说全程打掉关键点的个数，不会超过 \(p\) 的最长上升子序列和最长下降子序列长度之和，数据随机的情况下是 \(O(\sqrt n)\)，这样的话上述算法的复杂度就变成了 \(O(n^{1.5} \log n)\)！

P7450 [THUSCH2017] 巧克力

题意

一个 \(n\times m\) 的矩阵，格子 \((i,j)\) 有权值 \(a_{i,j}\) 与颜色 \(c_{i,j}\)，\(c_{i,j}=-1\) 表示这个格子不能选。

你要选择一个至少包含 \(k\) 种颜色的连通块，在最小化连通块大小的情况下，最小化连通块中权值的中位数。

\(n\times m \leq 233\), \(k\leq 5\), \(0\leq a_{i,j}\leq 10^6\)。

题解

只有 \(k\) 种颜色是好做的，对于中位数，我们二分答案，把小于的赋值为 \(-1\)，大于的赋值为 \(+1\)，然后一个格子的权值就是一个二元组 \((1,\pm 1)\)，跑斯坦纳树。

有很多种颜色，我们将颜色随机合并成 \(k\) 种然后做。这样子只要答案所用的 \(k\) 种颜色被划分到不同集合就 OK，浅算一下不可能低于 \(\dfrac{k!}{k^k}\)，多做几遍就完事。