结对编程-Core 第12组 [pb15061359+pb15061351]
一、项目要求
1.输入题目数量,生成操作数为3~5个的四则运算题目
2.输入上限值控制生成的操作数的最大值以及结果的最大值
3.输入支持的操作符类型:加、减、乘、除、乘方、括号
4.输入支持的操作数类型:整数,分数,小数
5.将上述功能封装成API接口提供给UI组使用
二、PSP
|
PSP2.1 |
任务内容 |
计划完成需要的时间(min) |
实际完成需要的时间(min) |
|
Planning |
计划 |
30 |
35 |
|
Estimate |
估计时间并做出规划 |
20 |
25 |
|
Development |
开发 |
1100 |
1200 |
|
Analysis |
需求分析 (包括学习新技术) |
30 |
20 |
|
Design Spec |
生成设计文档 |
10 |
10 |
|
Design Review |
设计复审 (和同事审核设计文档) |
10 |
30 |
|
Coding Standard |
代码规范 (为目前的开发制定合适的规范) |
5 |
5 |
|
Design |
具体设计 |
30 |
30 |
|
Coding |
具体编码 |
70 |
60 |
|
Code Review |
代码复审 |
20 |
30 |
|
est |
测试(自我测试,修改代码,提交修改) |
60 |
70 |
|
Reporting |
报告 |
40 |
50 |
|
Test Report |
测试报告 |
20 |
20 |
|
Size Measurement |
计算工作量 |
2 |
5 |
|
Postmortem & Process Improvement Plan |
事后总结 ,并提出过程改进计划 |
5 |
15 |
三、编程思路及遇到的问题
1.确定数据结构:
一开始打算使用一个结构体数组,以一个操作数、一个操作符的顺序随机生成中缀表达式。这种方式的生成、计算都没有大的问题,然而再括号的支持与否上比较麻烦。因为不仅要求是否生成括号,而且要求不能有多余的括号,如果使用生成中缀表达式的方法,并不利于对括号的处理。
最后决定使用二叉树的方式:第一个根节点必然存放操作符,接下来考虑左右子节点是存放操作数还是操作符。最后的规律为:所有子节点为操作数、根节点为操作符。节点定义为一个结构体,包含整形变量type:决定该节点存放操作符还是小数还是分数还是整数;整形变量data1放整数;float型data2放小数;结构体Fraction放分数;char型放操作符;该节点结构体指针,对应左节点、右节点。

typedef struct Fraction { int A = 0; // 整数部分 int B = 0; //分子 int C = 1; //分母 }Fraction; typedef struct TNode { int type;//决定放入操作数还是操作符 int data1 = 0;//放整数 float data2 = 0;//小数 Fraction fenshu;//分数 char signal = '\0';//操作符 struct TNode *lchild, *rchild;//左右节点 }TNode;
2.递归遍历生成二叉树:
此部分由于之前在数据结构上已有基础故完成的较快。
领航者对整个递归的逻辑、顺序作出合理的推演判断,驾驶者根据提出的大致顺序(递归的位置很重要)补全申请空间、初始化值的细节。由于操作数数量为3~5,所以只要生成固定层数为5的二叉树即可。

void InitTree(TNode* &T, int temp)//创建5层二叉树 { T = (TNode*)malloc(sizeof(TNode)); T->type = -1; temp++;//记录层数 if (temp<5)//小于5层继续递归 InitTree(T->lchild, temp);//左节点 if (temp<5) InitTree(T->rchild, temp);//右节点 if (temp == 5) { T->lchild = NULL; T->rchild = NULL; } return; }
3.放入随机操作数及操作符:
定义全局变量数组Operator_type[6],其对应加、减、乘、除、乘方、括号,1表示支持,0表示不支持。随机生成0~5的随机数,若对应的Operator_type[x]等于0,则需要再次生成x,直到满足为1。
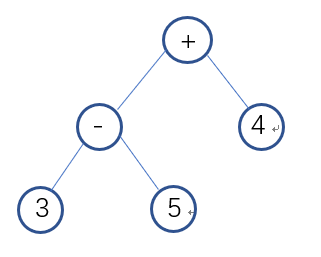
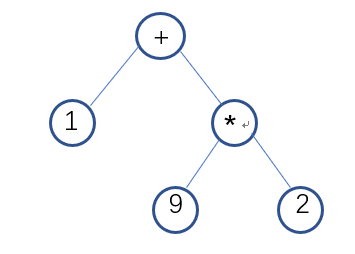
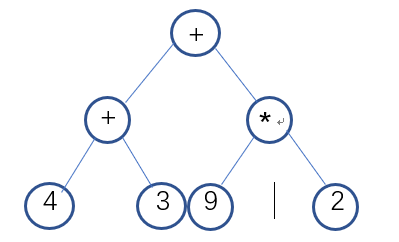
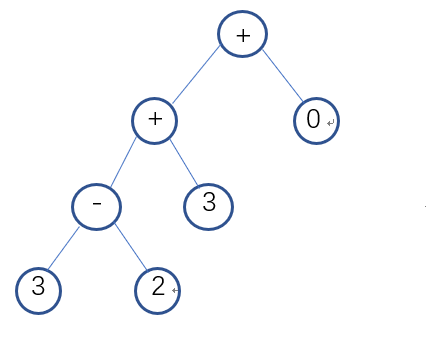
领航者作出对整个流程的设计:在Generate函数中,调用递归实现的Put_Number以及Put_Operator函数。其中对Put_Operator函数具体设计,根据随机操作数的不同,有不同的放入操作符的方式(先放入操作符,再用操作数补全所有子节点):如果是2个操作符,则有2种放入操作符的方式;如果是3个,则有5种;如果是4个,则有12种:4个操作符分别在一层,4个中2个操作符在第二层或者2个操作符在第三层,见图(部分可能性)。对此,通过定义三个全局变量数组:two[2][2]、three[5][4]、four[12][5],数组值为0代表放左节点,1代表放右节点,2代表回到根节点,-1代表为空。根据操作数选择对应的二维数组,再随机一种放入的方式,按照此方式遍历放入符合规定的随机操作符。倘若生成乘方,则需要立即对右节点赋值2~3,并通过置标志变量,不再生成乘方。
驾驶者根据流程做具体细化,并编写对应的需要调用的子函数并且直接编写Put_Number函数:定义全局变量数组Number_type[3],对应整数、小数、分数,支持则为1,不支持为0。随机0~2的随机数,若对应Number_type[x]等于0则需要再次生成x,直到满足为1。再根据x的,调用生成随机操作数的函数,random_int、random_float、random_fenshu,此三个函数分别返回对应类型的操作数。其中分数由自定义结构体Fraction规定。
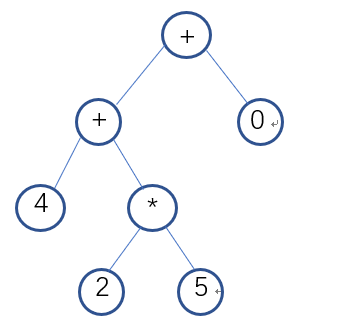
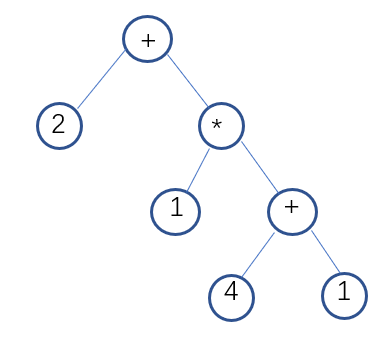
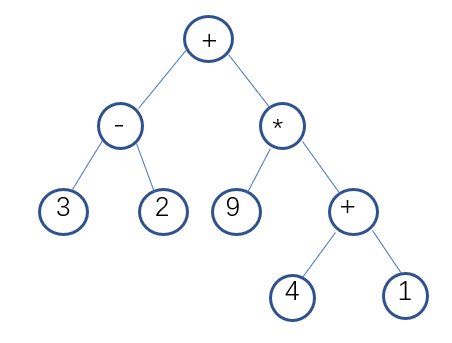
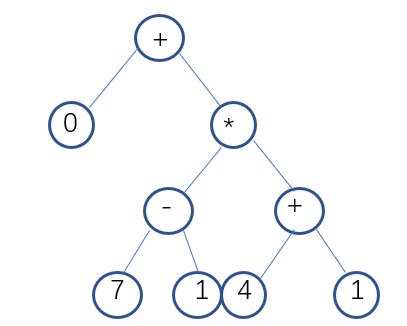

void Put_Operator(int str[]) {//往数中放操作符 int i = 0; TNode*p; //printf("str is %d %d", str[0], str[1]); p = T;//避免函数中的操作破坏了原来的根节点 p->signal = getSignal(Siganl_type);//根节点必放入操作符 p->type = 3; while (str[i] != -1) { if (str[i + 1] == -1 && Siganl_type[4] == 1 && rand() % 2 == 1) { if (str[i] == 0) { p->lchild->signal = '^'; p->lchild->type = 3; p->lchild->rchild->data1 = 2 + rand() % 2; p->lchild->rchild->type = 0; } if (str[i] == 1) { p->rchild->signal = '^'; p->rchild->type = 3; p->rchild->rchild->data1 = 2 + rand() % 2; p->rchild->rchild->type = 0; } i++; } else if (str[i] == 0) { //printf("put in left"); p->lchild->signal = getSignal(Siganl_type);//p首先是根结点,此时对左子节点赋值 p->lchild->type = 3; p = p->lchild; i++; } else if (str[i] == 1) { //printf("put in right"); p->rchild->signal = getSignal(Siganl_type); p->rchild->type = 3; p = p->rchild; i++; } else if (str[i] == 2)//p退回根节点 { p = T; i++; } } } void Put_Number(TNode* T, int Str[], int number_number, int end) { TNode*p; int number_count, x; p = T; if (p->lchild->type == -1) { do { x = rand() % 3; } while (Str[x] == 0); p->lchild->type = x;//根据x值放入对应类型的数据 switch (x) { case 0:p->lchild->data1 = random_int(0, end); break; case 1:p->lchild->data2 = random_float(0, end); break; case 2:p->lchild->fenshu = random_fenshu(end); p->lchild->fenshu = reduce_fenshu(p->lchild->fenshu); break; default:break; } } else if (p->lchild->type == 3) { Put_Number(p->lchild, Number_type, number_number, end); } if (p->rchild->type == -1) { do { x = rand() % 3; } while (Str[x] == 0); p->rchild->type = x; switch (x) { case 0:p->rchild->data1 = random_int(0, end); break; case 1:p->rchild->data2 = random_float(0, end); break; case 2:p->rchild->fenshu = random_fenshu(end); p->rchild->fenshu = reduce_fenshu(p->rchild->fenshu); break; default:break; } } else if (p->rchild->type == 3) { Put_Number(p->rchild, Number_type, number_number, end); } } int Generate(int setting_error) { float result_float = 0; int i, x_Signaltype = 0;; Fraction result, test; FILE* fp, *fp_key; srand((unsigned)time(NULL)); InitTree(T, 0); if ((fp = fopen("result.txt", "w")) == NULL) printf("error open file !!"); if ((fp_key = fopen("key.txt", "w")) == NULL) printf("error open file !!"); if (setting_error == -1) { printf("error setting\n"); return -1; } for (i = 1; i<question_number + 1; i++) { num_num = 3 + rand() % 3; if (num_num == 5) { x_Signaltype = rand() % 12; Put_Operator(four[x_Signaltype]); } else if (num_num == 4) { x_Signaltype = rand() % 5; Put_Operator(three[x_Signaltype]); } else if (num_num == 3) { x_Signaltype = rand() % 2; Put_Operator(two[x_Signaltype]); } Put_Number(T, Number_type, num_num, end); result = Calculate(T); result = reduce_fenshu(result); if (Number_type[1] == 1) { result_float = (float)result.A + ((float)result.B) / ((float)result.C); } if (result_float >=20) wrong = 1; if (result.A>=end||result.C>=end) wrong=1; if (wrong == 1) i--; else { checkforbkt(T); if (bktornot == 0) { //fprintf(fp, "%d.\t", i); inOrder(T, fp); fprintf(fp, " =\n"); if (Number_type[1] == 1) { fprintf(fp_key, "%0.2f\n", result_float); } else if (Number_type[2] == 1 && result.B != 0) { if(result.A!=0) fprintf(fp_key, "%d'%d/%d\n", result.A, result.B, result.C); else fprintf(fp_key, "%d/%d\n", result.B, result.C); } else fprintf(fp_key, "%d\n", result.A); } else i--; } wrong = 0; bktornot = 0; Empty(T); } fclose(fp); fclose(fp_key); printf("success!\n"); return 1; }
4.递归遍历生成中缀表达式:
遇到的一个问题就是在中序遍历时,一开始以为只要是根节点对应操作符的优先级大于右节点的操作符的优先级,则应该补上括号。仅仅这样的判断后确实省略去了加法、和乘方上多余的括号,如1+(2+3)这种式子是不会生成的。然而由于没有计算结果,所以对所有的除法、减法的括号没有作出正确的判断,如1-(2-3)这不是多余括号,这样简单的判断将导致它的括号也被舍去,变成1-2-3。不对比后序遍历计算的结果无法发现这样的错误,所以直到Calculate的函数写完后才发现这个问题。最后的修改就是对根节点操作符优先级大于右节点还要作出补充:当两者都是除法或者减法时,需要补充括号。
生成题目后,如果Operator_type[5]=0,即不支持括号,则调用checkforbkt函数,同样中序遍历的方法,判断是否有括号,由此决定是否舍弃此题。这个函数原理同中序遍历输出,不用执行写入操作,直接给标志变量bktornot即可。
领航者具体推演递归传入左节点、右节点的位置和条件以及大致递归流程,驾驶者对是否加入括号进行判定并补全具体流程下的赋值、写入操作。

void inOrder(TNode *p, FILE *fp) //中序遍历,同时输出不带荣誉括号的中缀表达式 { if (p) { if (p->lchild) { //如果当前节点的左子树 是运算符,且运算符优先级低于当前运算符,那么左边表达式要先计算,需加括号 if (p->lchild->type == 3 && getOperOrder(p->signal) - getOperOrder(p->lchild->signal)>1) { // printf("( "); fprintf(fp, "("); inOrder(p->lchild, fp); // printf(" )"); fprintf(fp, ")"); } //否则直接输出左子树 else inOrder(p->lchild, fp); } if (p->type == 0) { // printf("%d", p->data1); fprintf(fp, "%d", p->data1); } else if (p->type == 1) { // printf("%0.2f", p->data2); fprintf(fp, "%0.2f", p->data2); } else if (p->type == 2) { if (p->fenshu.A == 0) { // printf("%d/%d", p->fenshu.B, p->fenshu.C); fprintf(fp, "%d/%d", p->fenshu.B, p->fenshu.C); } else { // printf("%d'%d/%d", p->fenshu.A, p->fenshu.B, p->fenshu.C); fprintf(fp, "%d'%d/%d", p->fenshu.A, p->fenshu.B, p->fenshu.C); } } else if (p->type == 3) { // printf(" %c ", p->signal); fprintf(fp, " %c ", p->signal); } if (p->rchild) { if (p->rchild->type == 3 && getOperOrder(p->rchild->signal)<getOperOrder(p->signal)) { // printf("( "); fprintf(fp, "("); inOrder(p->rchild, fp); // printf(" )"); fprintf(fp, ")"); } else if (p->rchild->signal == '/'&&p->signal == '/'&&p->rchild->type == 3) {//除法与减法需单独再作判断 // printf("( "); fprintf(fp, "("); inOrder(p->rchild, fp); // printf(" )"); fprintf(fp, ")"); } else if (p->rchild->signal == '-'&&p->signal == '-'&&p->rchild->type == 3) { // printf("( "); fprintf(fp, "("); inOrder(p->rchild, fp); // printf(" )"); fprintf(fp, ")"); } else inOrder(p->rchild, fp); } } }
5.递归后序遍历并且计算:
由于三种类型的操作数混在一起时分类型计算十分麻烦,要考虑两个操作数类型的可能性并且分别写不同的函数。所以最后决定将整数、小数全部转化为分数类型,把两个分数类型的操作数传入Calculate函数中进行计算。分数由自己定义的结构体Fraction表示,其中包含3个变量,A,B,C分别对应整数部分,分子,分母。计算则统一采用通分计算,如果计算过程中任何部分出现负数或者分母为0,则将全局变量wrong置为1,当整个题目生成后,若wrong为1,则舍弃此题。
同时也需要约分的函数,用辗转相除法找到分子分母的最大公约数再除即可,这部分较为简单。整体流程是后序递归每个节点,每次Calculate函数接受一个节点指针并返回对应的操作数值。将一个操作符节点的左节点对应操作数、右节点操作数和该节点的操作符放入Operator函数进行计算。后序遍历,从最左下角开始返回值
,当前指针指向的是操作符,且左右节点是操作数。

Fraction Operate(Fraction a, char op, Fraction b)//分数的运算 { Fraction result; // printf("start to operate \t"); switch (op) { case'+':result.B = a.B*b.C + b.B*a.C; if (result.B<0) wrong = 1; result.C = a.C*b.C; if (result.C<0) wrong = 1; if (result.B >= result.C) { result.A = a.A + b.A + 1; result.B = result.B - result.C; } else result.A = a.A + b.A; break; case'-':if (((a.A*a.C + a.B)*b.C - (b.A*b.C + b.B)*a.C) < 0) { wrong = 1; result.A = 1; result.B = 0; result.C = 1; } else { result.B = (a.A*a.C + a.B)*b.C - (b.A*b.C + b.B)*a.C; if (result.B<0) wrong = 1; result.C = a.C*b.C; if (result.C<0) wrong = 1; result.A = result.B / result.C; result.B = result.B - result.C*result.A; } break; case'*':result.C = a.C*b.C; if (result.C<0) wrong = 1; result.B = (a.A*a.C + a.B)*(b.A*b.C + b.B); if (result.B<0) wrong = 1; result.A = result.B / result.C; result.B = result.B - result.C*result.A; break; case'/':if (b.A == 0 && b.B == 0) wrong = 1; else { result.C = a.C*(b.A*b.C + b.B); if (result.C<0) wrong = 1; result.B = b.C*(a.A*a.C + a.B); if (result.B<0) wrong = 1; result.A = result.B / result.C; result.B = result.B - result.C*result.A; } if (Number_type[0] == 1 && Number_type[1] == 0 && Number_type[2] == 0 && result.B != 0) wrong = 1; break; case'^':if (b.A == 2) { result.C = a.C*a.C; if (result.C<0) wrong = 1; result.B = (a.A*a.C + a.B)*(a.A*a.C + a.B); if (result.B<0) wrong = 1; result.A = result.B / result.C; result.B = result.B - result.C*result.A; } else if (b.A == 3) { result.C = a.C*a.C*a.C; if (result.C<0) wrong = 1; result.B = (a.A*a.C + a.B)*(a.A*a.C + a.B)*(a.A*a.C + a.B); if (result.B<0) wrong = 1; result.A = result.B / result.C; result.B = result.B - result.C*result.A; } break; } //if (wrong == 1)//有wrong说明计算过程中出现了负数或分母为0 //printf("wrong exp\n"); //printf("%d'%d/%d %c %d'%d/%d \n= %d'%d/%d\n", a.A, a.B, a.C, op, b.A, b.B, b.C, result.A, result.B, result.C); return reduce_fenshu(result); } Fraction Calculate(TNode *T)//后序遍历计算 { TNode *p = T; Fraction int_f, a, b, result; if (p != NULL && p->type == 0) {//将整数转化为分数 int_f.A = p->data1; int_f.B = 0; int_f.C = 1; return int_f; } else if (p != NULL && p->type == 2) return p->fenshu; else if (p != NULL && p->type == 1)//将小数转化为分数 return change_to_fraction(p->data2); else { a = Calculate(p->lchild);//遍历至左节点操作数 b = Calculate(p->rchild);//遍历至右节点操作数 result = Operate(a, p->signal, b);//分数运算 return result; } }
6.接口设计:
向外部提供的是一个结构体,两个函数。结构体Parameter用于设定部分参数,其中包括是否支持整数、小数、分数、加减乘除乘方括号,支持则对应变量置为1,否则为0。其设定完毕后传入Setting_Parameter函数用于接受设定的三个参数,第一个为题目数,第二个为上界,第三个即为Parameter的结构体变量。该函数对接受的设定参数进行一定的判断,不符合则返回-1,否则返回1,将返回的值再放入Generate函数中生成题目和答案到result.txt和key.txt中,若为-1,则不会执行Generate函数。
以.cpp和.h生成了x86和x64的.dll和.lib。生成方式:VS中建立dll工程,.cpp放入主要代码并去掉main函数,.h中对接口函数、结构体作声明,再生成即可。
与第11组对接时,由于是第一组所以对dll的调用还很陌生,使用了很多方法,出现过无法解析函数、无法连接.lib等问题。最后采用添加.h文件,并include在主函数中,再将.lib和.dll文件放在工程当前目录工作目录下,加入#pragma comment(lib,"x:\xx\xx\Core_x64,lib")绝对路径的方法成功对接。
与第10组对接时,反映说Setting(之前是这么命名的)函数和他们定义的某个类重名了。想了一下Setting的函数名确实过于简单容易重名,所以索性改的长一些Setting_Parameter(),一来不重名、二来更能表达作用。还有一点就是对方反映会输出0‘1\2这样的分数,我们回去查看了一下代码发现在测试与0有关的bug的时候把判断句注释掉了,于是赶紧去掉注释再测试不再出现这样的问题。
与第3组对接时,反映说不知道我们对于参数输入错误时的打印在哪里(我们在说明文档中提到参数错误会打印出”error xxx“)。想了一下当时是想做个简单的入口检测避免数组上的越界崩溃,不过想的简单了仅仅用了printf。虽然参数错误Setting_Parameter函数会返回-1不再执行Generate函数,不过简单的printf在运行exe下可并不会出来,算是想简单了白写了printf。好在UI组能力强可以根据我们的说明自己做入口检测。

typedef struct Parameter { //该结构体用于设置用户要求的参数,传给Setting函数用于生成对应要求的题目 int integer = 1; //支持 整数 生成则为1,不支持则为0,默认为支持 int decimal = 0; //支持 小数 生成则为1,不支持则为0,默认为不支持 int fraction = 0; //支持 分数 生成则为1,不支持则为0,默认为不支持 int add = 1; //支持 加法 符号生成则为1,不支持则为0,默认为支持 int sub = 1; //支持 减法 符号生成则为1,不支持则为0,默认为支持 int multiply = 1; //支持 乘法 符号生成则为1,不支持则为0,默认为支持 int division = 1; //支持 除法 符号生成则为1,不支持则为0,默认为支持 int pow = 0; //支持 乘方 符号生成则为1,不支持则为0,默认为不支持 int bracktet = 1; //支持 括号 符号生成则为1,不支持则为0,默认为支持 }Parameter; int Setting_Parameter(int question_num, int sup, Parameter argument) { if (question_num != 0) question_number = question_num; else if (question_num < 0) { printf("error question number\n"); return -1; } if (sup != 0 && sup >= 1) end = sup; else if (sup <= 1) printf("wrong sup!\n"); /* if (argument.Data_Number != 0 && argument.Data_Number >= 3 && argument.Data_Number <= 5) num_num = argument.Data_Number; else if (argument.Data_Number < 3 || argument.Data_Number>5) { printf("error count of number\n"); return -1; }*/ if (argument.integer == 1 || argument.integer == 0) Number_type[0] = argument.integer; else { printf("error integer input!\n"); return -1; } if (argument.fraction == 1 || argument.fraction == 0) Number_type[2] = argument.fraction; else { printf("error fraction input!\n"); return -1; } if (argument.decimal == 1 || argument.decimal == 0) Number_type[1] = argument.decimal; else { printf("error decimal input!\n"); return -1; } if (argument.integer == 0 && argument.decimal == 0 && argument.fraction == 0) { printf("至少支持一种类型的数\n"); return -1; } if (argument.add == 1 || argument.add == 0) Siganl_type[0] = argument.add; else { printf("error add permission!\n"); return -1; } if (argument.sub == 1 || argument.sub == 0) Siganl_type[1] = argument.sub; else { printf("error subtraction permission!\n"); return -1; } if (argument.multiply == 1 || argument.multiply == 0) Siganl_type[2] = argument.multiply; else { printf("error multiple permission!\n"); return -1; } if (argument.division == 1 || argument.division == 0) Siganl_type[3] = argument.division; else { printf("error division permission!\n"); return -1; } if (argument.pow == 1 || argument.pow == 0) Siganl_type[4] = argument.pow; else { printf("error mtp2 permission!\n"); return -1; } if (argument.bracktet == 1 || argument.bracktet == 0) Siganl_type[5] = argument.bracktet; else { printf("error plus permission!\n"); return -1; } if (argument.add == 0 && argument.sub == 0 && argument.multiply == 0 && argument.division == 0) { printf("error operator permission!\n"); return -1; } return 1; }
四、运行结果
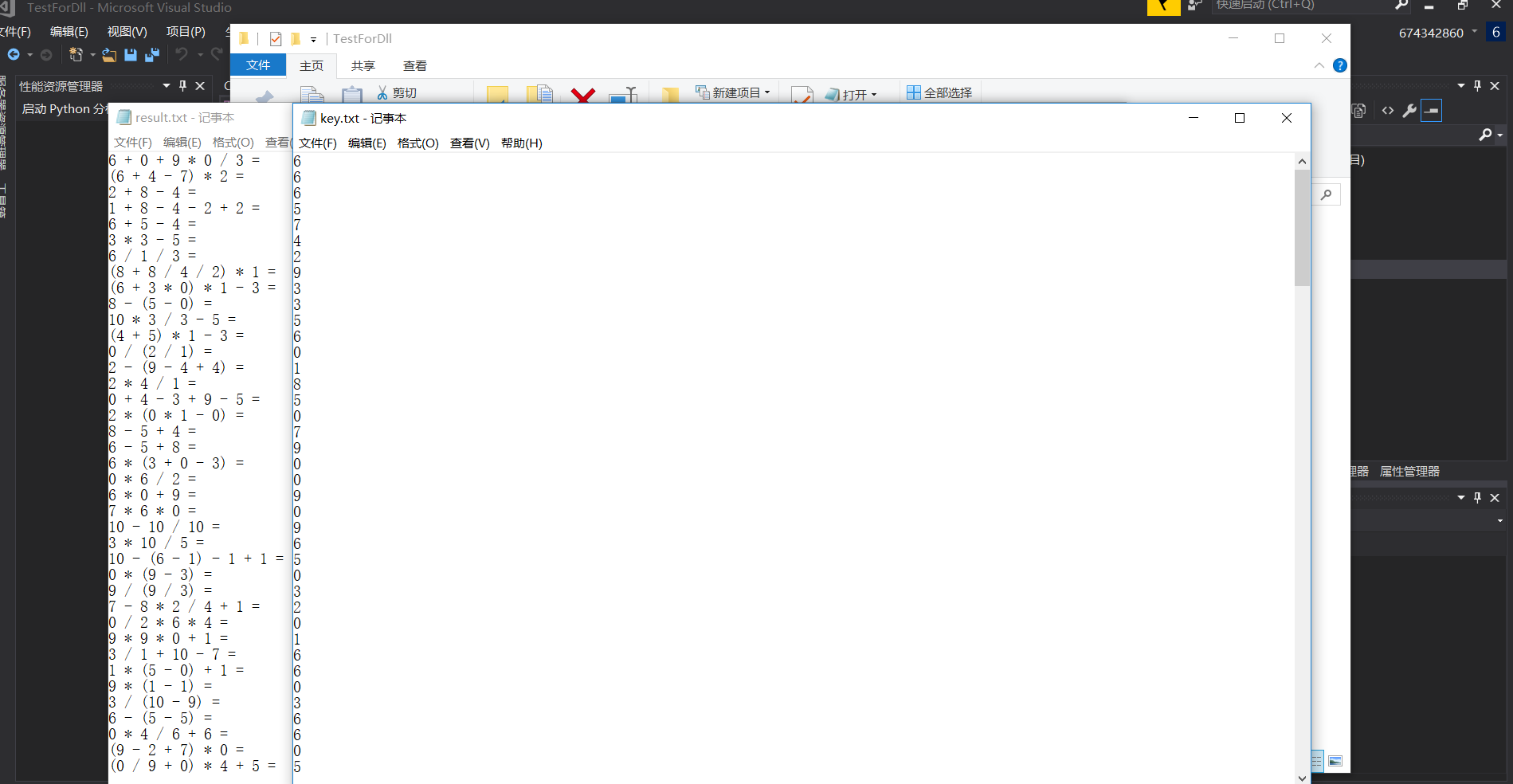
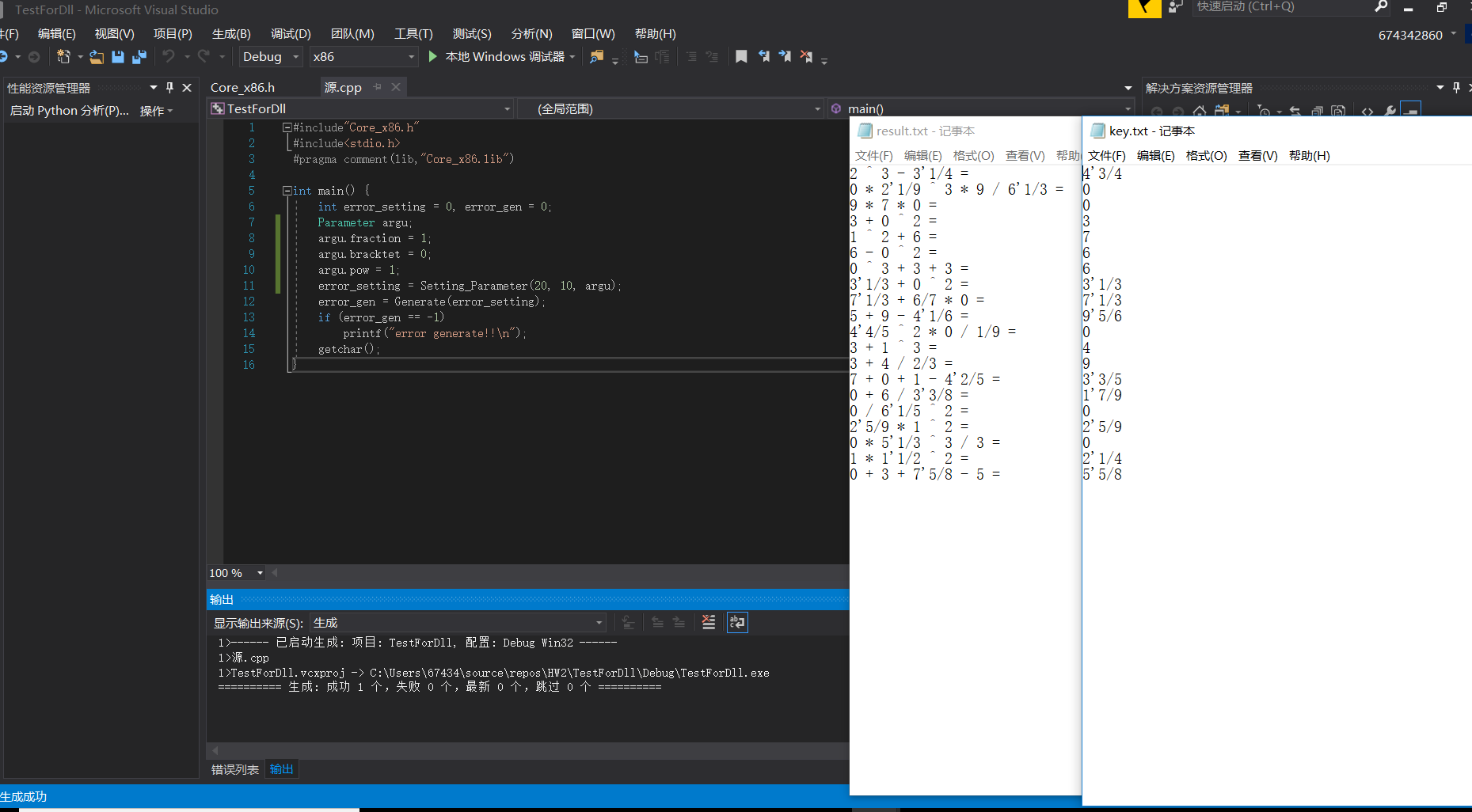
生成dll后按照之前所述方法自己重新写了测试的接口,以下是结果
1.直接传入默认值的Parameter(整数,加减乘除括号),题目数200,上界10:
2.设定20道,上界10,支持整数、分数,加减乘除乘方,不支持括号:
五、结对感想
1.结对首先在花的时间上就小于一个人,原因是和队友一起讨论题目要求、制定方案可行性,远比一个人效率高。而且在写程序的时候,首先领航员在一旁监督能极大的减少手误。并且出现bug时,两个人一起思考流程,找出错误原因的效率高于一个人。
2.有的时候虽然会出现流程设计上的分歧,但是不同的设计方案,反而拓宽了思路。并且如果之后要重构,也可以快速的采用另一种方案。
3.结对编程乐趣大于一个人,成功可以一起分享喜悦。而失败之时,两个人可以一起努力。
六、github地址:https://github.com/674342860qq/PW1




