拓扑排序
定义
之前介绍了图的基本概念，BFS和DFS，在理解之前内容的基础上再学这个就比较简单了。
- 啥？
- 图还能排序？
- 什么是拓扑排序？
拓扑排序只是针对特殊的有向图才能进行的排序方法，先放个课程先修图的例子，盗个图🐶。
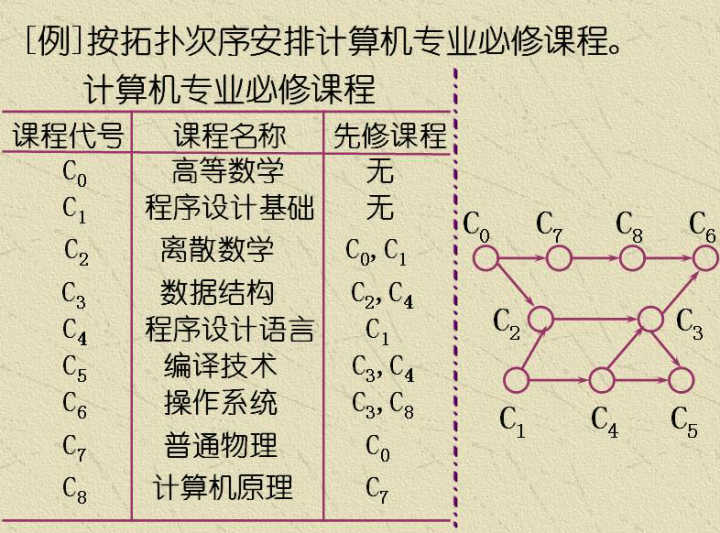
图中的每个顶点都代表一门学科，像这种某些顶点只能依赖于其他顶点已经完成之后才能开始的图称为依赖图或优先图。生活中的实例也是狠多的，想起以前一个脑经急转弯：每天起床第一件是啥？叠被子吗？哈哈，先睁眼，不睁眼怎么叠被子，怎么洗漱。话说回来，寻找这样一个顶点序列，使得每个顶点的依赖顶点都在其之前被访问，这样的过程就是拓扑排序。
实现思路
我们寻找顶点序列的过程就是给顶点进行编号的过程，保证被依赖顶点编号比依赖顶点的小，这样按照编号访问图就能满足条件。放个实例：
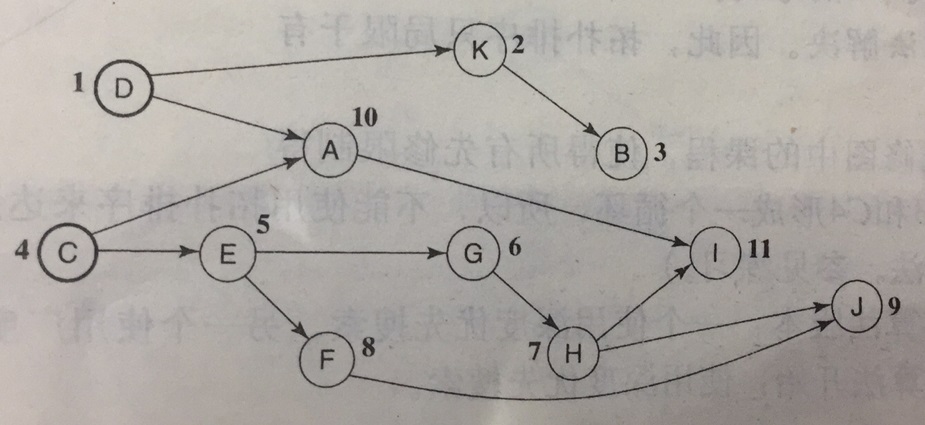
当然，如果有向图中出现了环也是没法进行拓扑排序的，所以确切的说拓扑排序只局限于有向无环图（DAG）。具体编号方法有两种，分别对应BFS和DFS算法。
BFS拓扑排序
BFS拓扑排序思想很简单，每个顶点在其所有前驱节点编号之后才能进行编号。在上图中，A的前驱节点是C和D，只有C和D编号结束之后才可以对A编号。
具体做法是对每个顶点的前驱节点进行计数，遍历前驱数量为0的顶点，每次便利后，将遍历顶点的后继节点的前驱数减1。下一轮再遍历前驱数为0的顶点，然后重复之前的过程。
用伪代码表示为：
1 BFStopsort 2 3 for each vertex v in graph do 4 compute pred(v),the preprocessor count of v; 5 end for 6 7 for each vertex v in graph do 8 if(pred(v)=0) then 9 add v to queue; 10 end if 11 end for 12 13 topnum ← 1; 14 while queue is not empty do 15 w ← vertex at front of queue; 16 delete w from queue; 17 number w with topnum; 18 topnum ← topnum + 1; 19 20 for each neighbor p of w do 21 pred(p) ← pred(p)-1; 22 if(pred(p)==0) then 23 add p to queue; 24 endif 25 end for 26 end while
注意，第2个for循环就已经把不同连通分支的前驱节点数为0的顶点加入队列了，所以这里不需要驱动器。
DFS拓扑排序
DFS拓扑排序的原理是 对节点v，其拓扑编号小于从v可以到达的所有顶点编号。另外在DFS扫描的过程中，只有v可以到达的所有顶点都访问之后，访问过程才从v返回。
所以这一编号过程是先利用DFS的原理一条路都到黑，也即无路可走，这时候给这个顶点最大的拓扑编号。然后向上退回一个顶点继续访问，直到无路可走，然后递减地给顶点编号。还是上面的例子：
从C顶点出发，一直走到I顶点，然后给其编号为11，再回退给A编号10,再退回到C顶点寻找其他路径。
What? 为什么要倒着编号？
假如出发点是A，上来就给A编号为1，那C的编号怎么办？所以倒着编号是最稳妥的方法。
伪代码实现如下：
1 DFStopsortdriver 2 topnum ← n; 3 4 for each vertex v in the graph do 5 if(v is not visited) then 6 DFStopsort(v, topnum); 7 end if 8 end for 9 10 11 DFStopsort(v, topnum) 12 visit v and mark v as visited; //先记录已访问 13 14 for each neighbor w of v do 15 if(w is not visited)then 16 DFStopsort(w, topnum); 17 end if 18 end for 19 20 number v with topnum; //后对其编号 21 topnum ← topnum-1;
注意这里是先标注顶点已访问，在从其返回的时候，也即其所有可到达的顶点都标记完成之后，才进行编号。
