BFS和DFS
引言
在上节,介绍了图的基本概念,还是举之前的例子,房间布局图:
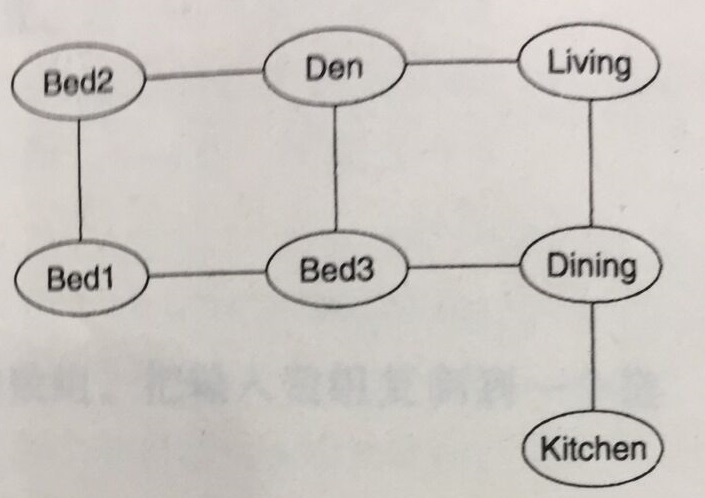
你想找到一条从Kitchen到Bed2的路径,这时候你必须要沿着某条边的序列走到Bed2,而且不经过任意房间超过一次。对于任意的图,在最坏情况下,编写这样的程序需要走遍整个图。这样的过程就是图的遍历。遍历的过程就是访问图中顶点的过程,在访问一个顶点的时候执行某个动作,动作可简单可复杂(不止是打印,更新,便于扩展)。
有两个大家耳熟能详的图遍历方法——BFS和DFS,正是本文介绍的主要内容。
BFS
BFS即广度优先搜索,其主要特征是它在图中涟漪式地访问顶点。以下图为例:
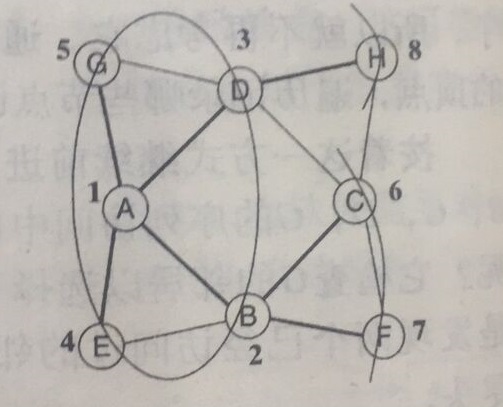
以A为涟漪起点,第一波访问其每一个邻居,第二波访问未访问过的邻居的邻居顶点,以后每一波依此类推,直到图中所有顶点访问完毕。说白了,依次访问距离起始顶点距离为1,2,3....的顶点。
如何实现?
BFS的实现是不是有点似曾相识?这不就是树的层级遍历的扩展吗?没错!实现起来原理也是一样的,利用队列,在遍历顶点的同时将其未遍历的邻居加入到队列中。一波访问结束,再将队列中的顶点取出,重复之前的操作。用《数据结构从应用到实现Java版》上一张图表示,如下:

这里必须维护一个数据结构,存储已经访问过的顶点信息,每次将顶点加入队列之前,检查顶点是否已被访问,避免重复操作。
鄙人自己也实现了一版,具体代码,见博文末尾。
DFS
DFS即深度优先搜索,沿着图中一条路径尽可能往深走到底,访问这条路径上的每个顶点,当无法前进的时候退回并尝试另个方向,同样尽可能深地前行。说白了就是一条道走到黑,直到无路可走了,再回退寻找下个访问节点,继续一条路走到黑。
还是上例,一张图。
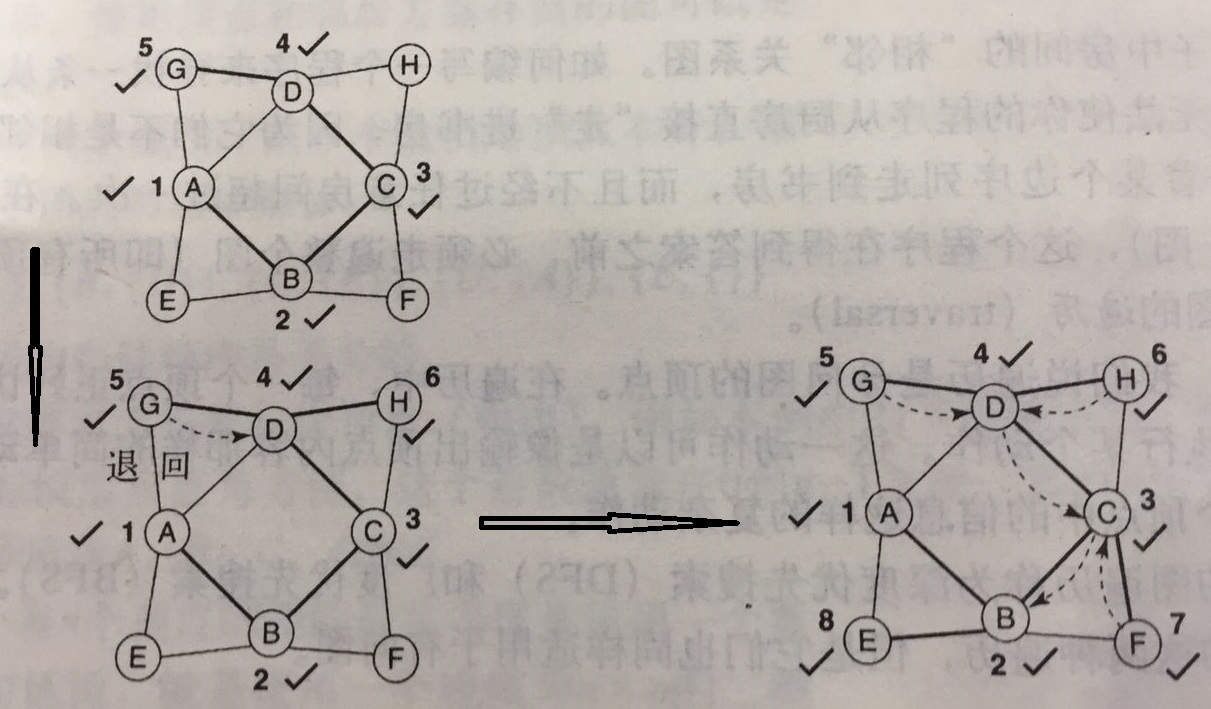
访问顺序如图,需要注意的是,使用DFS的时候,选择哪个顶点为下一个访问顶点依赖于邻居的存储顺序。这个例子中,是以字母表顺序存储邻居,所以遍历顺序如上。同样,也要维护一个数据结构,存储以遍历顶点信息。
DFS的使用可以使用递归,也可以使用栈。如果有同学对栈实现DFS感兴趣的话,不妨看一下,我之前的博文http://www.cnblogs.com/ustcwx/p/7756783.html 。
遍历驱动器
如果所有图都是无向连通图,那无论是BFS还是DFS,只要从任意一个顶点出发就可以遍历所有顶点。但遇到非连通图,或者弱连通有向图,怎么办?以地图为例:
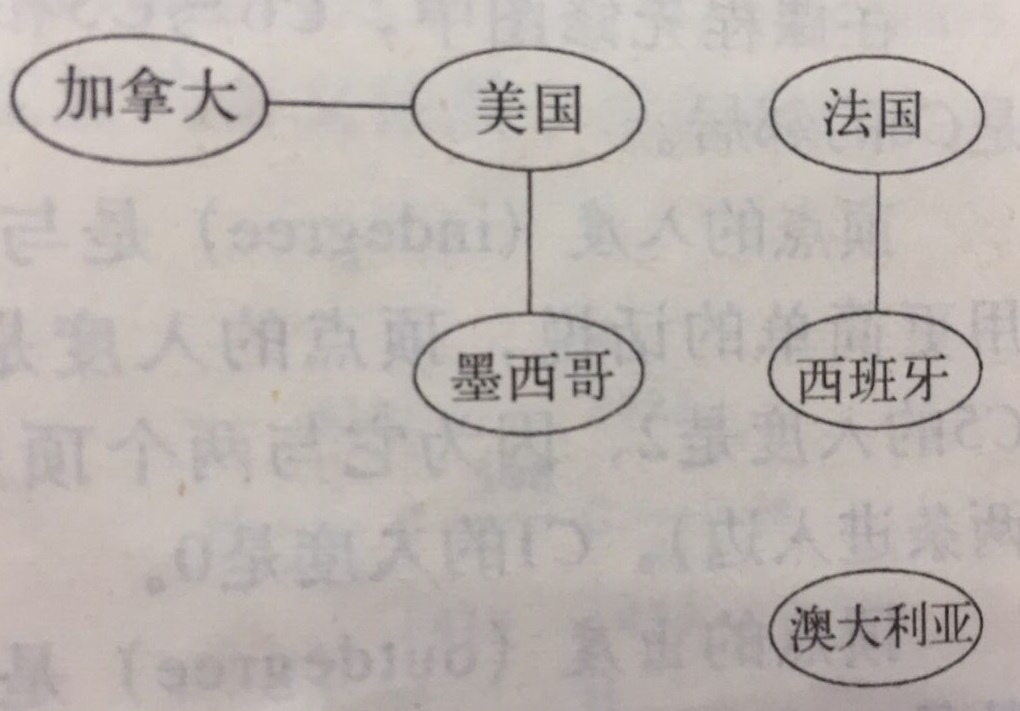
这个图至少要从三个顶点出发,才能遍历结束全部顶点。这时候我们就需要一个驱动器,对每个顶点检查是否已访问,对未访问的顶点调用遍历算法。用伪代码表示,如下:
1 XFSdriver 2 3 for each vertex v in the graph do 4 if(v is not visited) then 5 XFS(v) 6 end if 7 end for
时间复杂度
设图有v个顶点,e条边。无论是BFS还是DFS,遍历过程中,每个顶点有且只被访问一次,其区别仅在于顶点和边的扫描访问顺序不同。但是顶点会被检查若干次,即检查其是否已被访问过。检查多少次呢?访问每个顶点的时候都会检查其邻居,所以检查的时候是按照边的方向检查。无向图中e条边,对应有向图中的2e条边。所以无向图的时间复杂度为O(v+2e),而有向图的时间复杂度为O(v+e)。
如果把驱动器检查的次数也算上,无向图的时间复杂度为O(v+e)(由O(2v+2e)得到),而有向图的时间复杂度为O(2v+e)。
具体实现
其实实现不难,最初我也实现了功能,但总觉得代码有点怪。后来对比了大神的代码,发现还是接口设计得比较烂,设计模式功底不到家。代码后来又改了一版,这里摘抄另鄙人受益良多的两段话。
设计与接口
- 此类必须只做它应该做的事情,不多也不少。例如,深度优先搜索知道这个图,所以,它只负责以深度优先顺序遍历顶点。然而,它对使用它的软件不了解,所以,在访问一个顶点的时,它不能定义要做什么,这要留给这个软件。
- 此类必须富有弹性,必须允许用户有足够多的钩子,在此用户可以控制执行软件特化的动作。作为一个例子,我们知道,在深度优先搜索的前行阶段遇到一个顶点时,要标识这个顶点已见过。但是,看见一个顶点可以与访问这个顶点分开,而不影响深度优先搜索的正确性。
如果不太理解的话,可以接着看后续博文。言归正传,这里我把BFS和DFS写到一个类里面了,不要拍我啊,哈哈。
package com.structures.graph; import com.structures.linear.CircularQueue; import java.util.ArrayList; /** * Created by wx on 2018/1/9. * 使用递归实现邻接链表的BFS算法; * 使用队列实现邻接链表的DFS算法. */ public class XFS<T> { private ArrayList<Vertex<T>> processedVertex; //存储已遍历顶点 private ArrayList<Vertex<T>> graph; //构建好的邻接链表 private Visitor<T> visitor; //访问类 public XFS(myGraph<T> newGraph){ graph = newGraph.getVerList(); processedVertex = new ArrayList<Vertex<T>>(); visitor = new Visitor<T>(); } // 深度优先搜索驱动器 public void DFS(){ clear(); for(Vertex<T> vertex : graph){ if(!processedVertex.contains(vertex)) DFSTraverse(vertex); } } // DFS实际逻辑 private void DFSTraverse(Vertex<T> vertex){ visitor.visit(vertex); //操作节点 markVertex(vertex); //标记节点 for(int i=0; i<vertex.neighbors.size(); i++){ Vertex<T> nerVertex = graph.get(vertex.neighbors.get(i).index); if(!processedVertex.contains(nerVertex)) DFSTraverse(nerVertex); } } //将顶点标记为已处理 private void markVertex(Vertex<T> vertex){ if(!processedVertex.contains(vertex)) processedVertex.add(vertex); } //清除之前成员变量信息 private void clear(){ processedVertex = new ArrayList<Vertex<T>>(); } // 广度优先搜索驱动器 public void BFS(){ clear(); for(Vertex<T> vertex : graph){ if(!processedVertex.contains(vertex)) BFSTraverse(vertex); } } // BFS实际逻辑 private void BFSTraverse(Vertex<T> vertex){ CircularQueue<Vertex<T>> laterVertex = new CircularQueue<Vertex<T>>(graph.size()); laterVertex.enqueue(vertex); while(!laterVertex.isEmpty()){ //遍历访问过的一层顶点 Vertex<T> preVertex = laterVertex.dequeue(); visitor.visit(preVertex); markVertex(preVertex); for(int i=0; i<preVertex.neighbors.size(); i++){ //将顶点的邻居加入待访问队列 Vertex<T> nerVertex = graph.get(vertex.neighbors.get(i).index); if(!processedVertex.contains(nerVertex)) laterVertex.enqueue(nerVertex); } } } }
经测试,运行情况良好!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号