图的基本概念
图的组成
之前学习了很多树,而树只是特化了的图,仅模拟层次结构。不知道有多少人细看过《图论》,光是图书馆也很难找到特别多的专业书籍,读起来也是艰深晦涩。好在今天只是介绍一些基本概念,也请读者放松心态。
怎么模拟一张图?先放一张大家熟悉的地铁图:
我们模拟的目的是将图抽象出来,建立一个数学模型。就像函数一样,一个坐标唯一对应一个函数值。那么怎么建立这个模型,前人的经验是将图(graph)等价于顶点(vertex)和边(edge)的集合,也即G=(V,E)。当然,也许你有更好的办法,但是这种表示使用得最广泛,非常有学习的必要。
图的分类
大体上图可以分为两类,有向图和无向图,其区别在于相邻顶点之间的边是否有向。一句话概括,有向图模拟非对称关系,无向图模拟对称关系,无向图是特殊的有向图。
无向图
举个例子,一套房的各个房间的布局图:
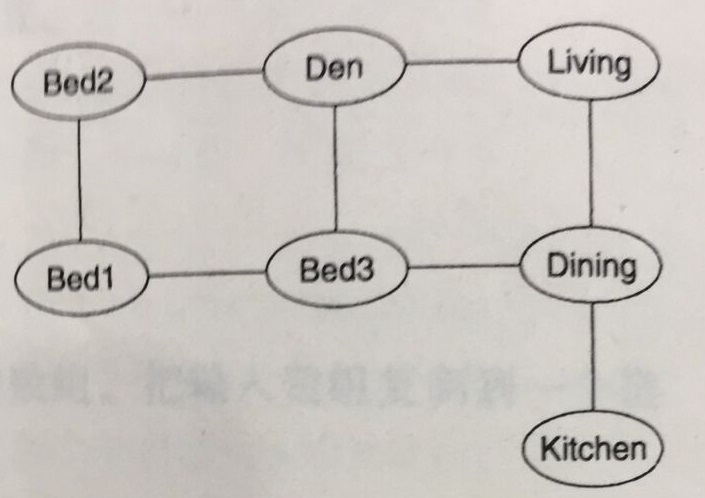
如上图,卧室1和卧室2之间的边就是没有方向的,或者说是双向的,可以用(Bed1, Bed2)或者(Bed2, Bed1)表示。
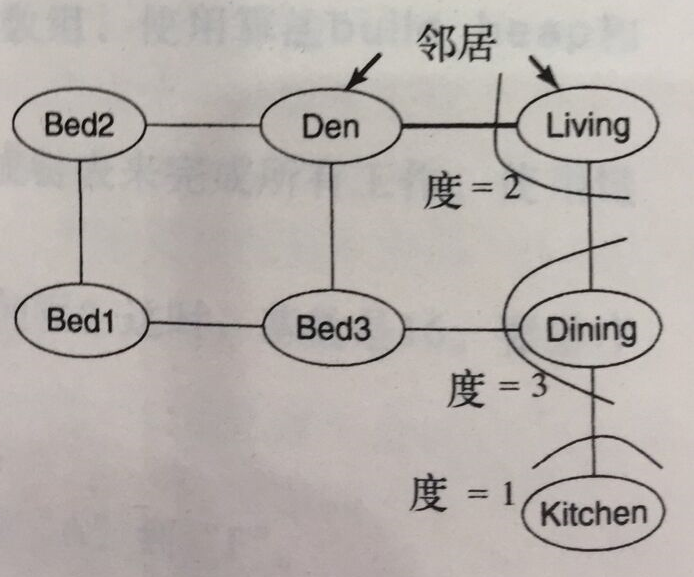
同样是这个例子,当两个顶点之间有边连接的时候,我们称一个顶点是另一个顶点的邻居。而一个顶点的度则是它的邻居的个数。
此外,我们看,在这个图中Bed1到Kitchen之间的路径,可以模拟成边的序列表示,此处路径不唯一,选择其中一条,表示为(Bed1,Bed3),(Bed3, Dining), (Dining, Kitchen)。如果一条路径既没有重复边,也没有重复顶点,我们称这样的路径为简单路径。在这个无向图中,存在环结构,即存在一条起始与终止顶点相同的路径。如Bed1,Bed2,Den,Bed3,Bed1。
说明一下图的连通性,如果图中所有顶点之间都存在路径,那么这个图即为联通图,反之为非连通图。以地图为例:
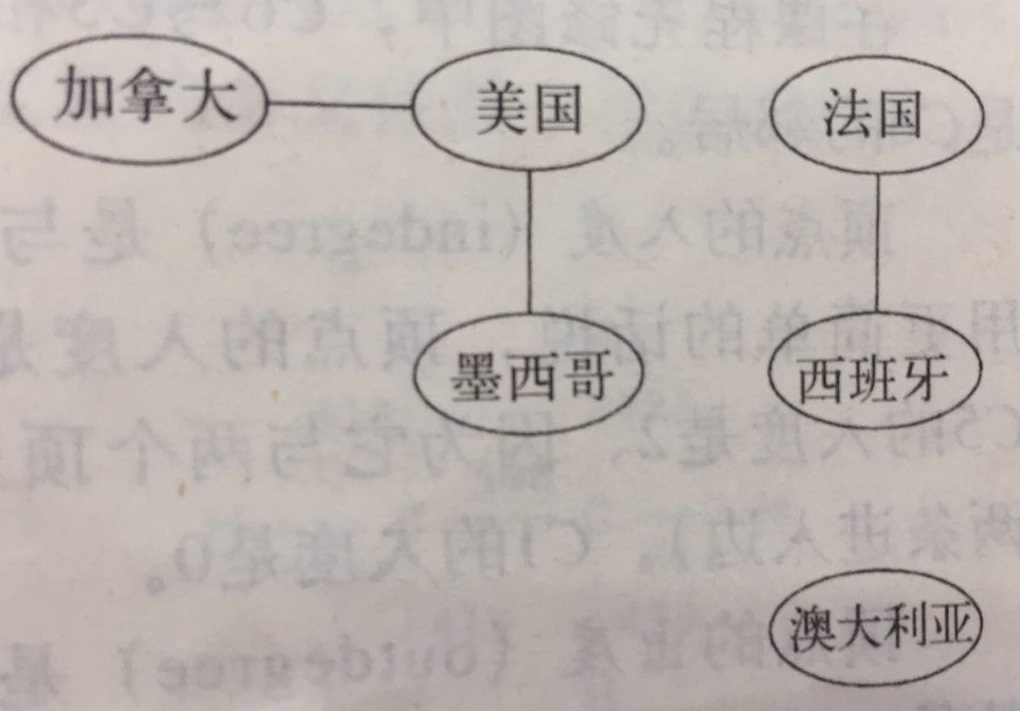
美国和澳大利亚因为不在一块大陆上,所以不存在路径,这就是一个非连通图。非连通图是一组分量,每个分量是一个子图,它自身是连通的,这些分量称为连通分支。上图中存在3个连通分支。
有向图
理解无向图的基础上再看有向图就简单很多了,先上例子,以大学课程先修结构为例:
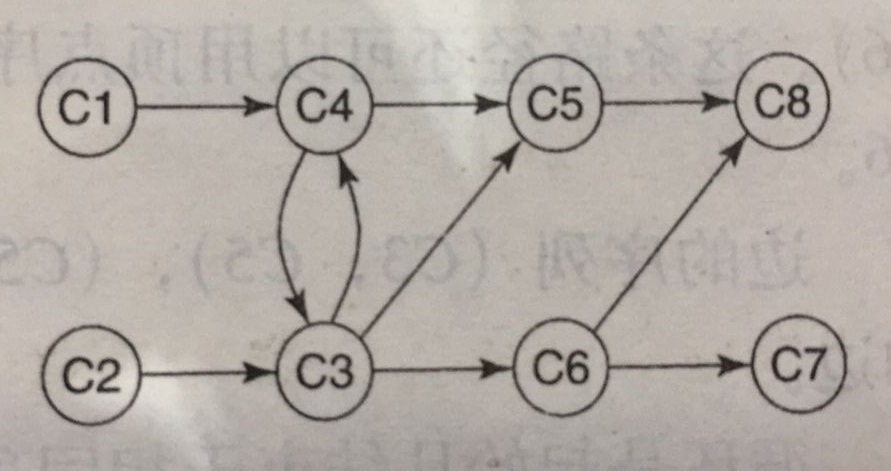
从C3到C5的有向边记为有序对(C3,C5),不同于无向图,在有向图中(C5,C3)与(C3,C5)是完全不同的概念,区别在于方向。(C3,C5)表示课程C3是C5的先修课程。注意,在这个例子中,C5是C3的邻居,而C3不是C5的邻居。
有些课程,诸如C3和C4是并修的关系,要表示这样的关系又不能用无向边,那么就用两条有向边代替。
在无向图中我们解释了度,而有向图中分为入度和出度,顶点的入度即是与它相邻的顶点数量,出度是它与之相邻的顶点数量。图中C5为例,其入度为2,出度为1。
加权图
加权图并非独立于无向图和有向图概念之外的一种图,其模拟边上带权的情况,类似于树中的Huffman树。放两张无向图和有向图中的加权图实例。
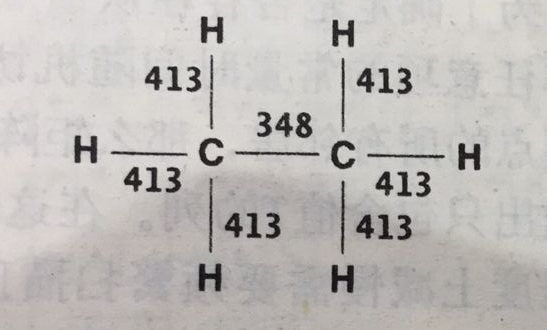
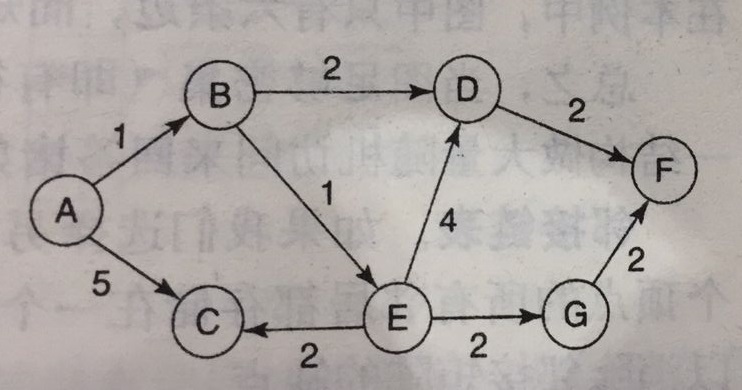
这种例子还有很多,最常见的就是地图上城市之间的关系,两个城市之间路径的长度就是其边的权重大小。
图的表示方法
刚学图的时候,没有看别人的方法,自己就钻研怎么表示图。想了很久,最后发现想出来的方法都被前人考虑过了,并没有得出更高效的解决方案。后来去查资料,发现就专门有人研究图的表示方法,还出过书,惭愧。图的表示方法很多,现在用的最多方法有两种,一种是邻接矩阵表示,一种是邻接链表表示。需要说明的是,这两种方法对有向图无向图的表示通用。
以一个有向图为例:
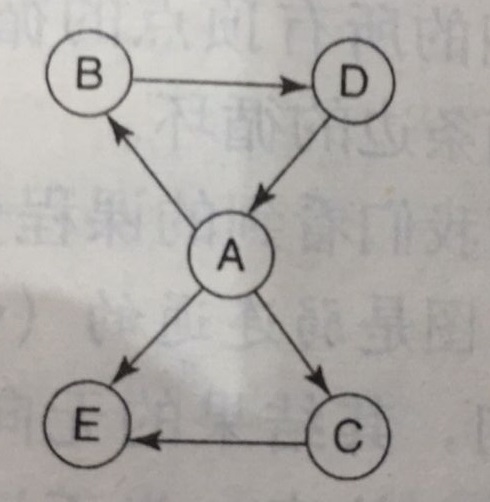
邻接矩阵
对包含n个顶点的图,使用规模为n*n的数组去模拟,上图模拟结果如下:
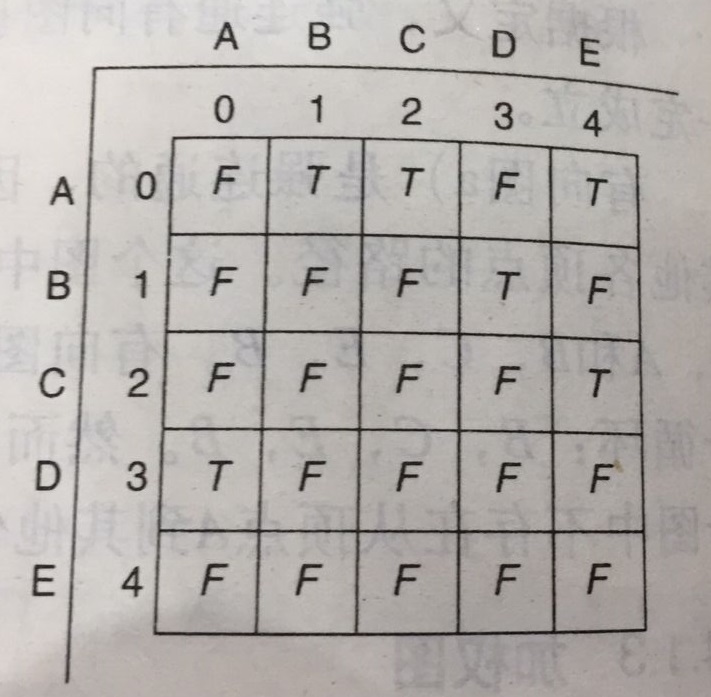
看到这个图,估计大家心里都有数了,不赘述了。
- 那么这种表示方法有什么好处和弊端?
数组的好处是可以随机访问,如果想直接知道两个顶点之间是否有边的关系,O(1)的时间复杂度就可以做到查询;弊端是,可能浪费空间,如果要知道一个顶点的所有邻居,就要遍历规模为n的数组,时间复杂度为O(n)。当经常有查询邻居关系的需求,或者图足够密集(边足够多)的时候,这种表示方法是比较有用的。反之则低效。
邻接链表
这种方式将顶点所有邻居存放在一个链表中,还是上面的实例,其表示如下:
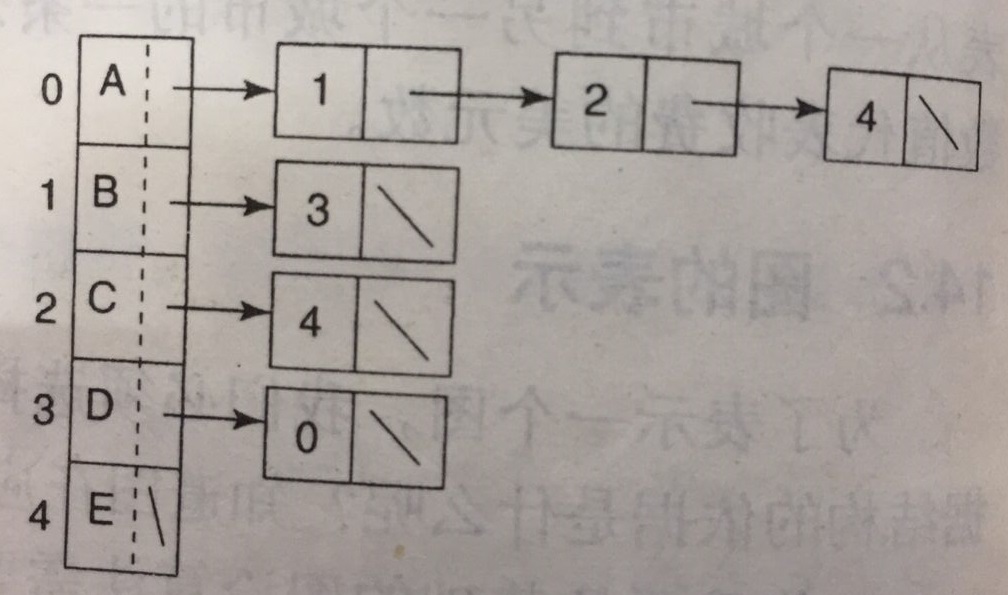
- 同样的,有什么优点和弊端?
相比与链接矩阵,邻接链表的空间利用率更高一点,但是做不到邻接矩阵那样的随机访问,如果需要知道一个顶点的邻居中是否包含另一个顶点,就要遍历其所有邻居。同样的,如果想知道一个顶点的所有邻居,直接遍历其邻居链表,没有冗余的检查,避免了时间的浪费。
写在图表示之后
发现没有,即使是大名顶顶的图,在计算机中的表示,最终也只归为两类,数组结构和链式结构,和我们之前学的树,堆栈,没有什么区别,所以夯实基础是非常重要的,即使做不到一通百通,至少举一反三是很轻松的。
图代码
鄙人实现了一版,又参照大神的改动了一下,最终得到如下代码:
1 package com.structures.graph; 2 3 import java.util.ArrayList; 4 5 /** 6 * Created by wx on 2018/1/9. 7 * 此处使用邻接链表的形式表示图,此类为图构造类. 8 */ 9 public class myGraph<T> { 10 private ArrayList<Vertex<T>> verList; 11 12 // 构造器中完成图的邻接链表表示 13 myGraph(T[] dataArray, int[][] neighborArray){ 14 check(dataArray, neighborArray); 15 verList = new ArrayList<Vertex<T>>(dataArray.length); 16 initialize(dataArray, neighborArray); 17 } 18 19 private void check(T[] dataArray, int[][] neighborArray){ 20 if(dataArray.length!=neighborArray.length) 21 throw new GraphViolationException("Error parameters!"); 22 } 23 24 private void check(T[] dataArray, int[][] neighborArray, int[][] weight){ 25 if((dataArray.length!=neighborArray.length)||(dataArray.length!=weight.length)) 26 throw new GraphViolationException("Error parameters!"); 27 } 28 29 // 构造带权重图 30 myGraph(T[] dataArray, int[][] neighborArray, int[][] weight){ 31 check(dataArray,neighborArray,weight); 32 verList = new ArrayList<Vertex<T>>(dataArray.length); 33 initializeWeight(dataArray, neighborArray, weight); 34 } 35 36 //初始化数组及每个元素对应的邻接链表 37 private void initialize(T[] dataArray, int[][] neighborArray){ 38 for(int i=0; i<dataArray.length; i++){ 39 Vertex<T> myVertex = new Vertex<T>(dataArray[i]); 40 41 if(!verList.contains(myVertex)) { 42 for (int j = 0; j < neighborArray[i].length; j++) { 43 myVertex.addNeighbor(new Neighbor(neighborArray[i][j])); 44 } 45 verList.add(myVertex); 46 } 47 } 48 } 49 50 //初始化带权重图 51 private void initializeWeight(T[] dataArray, int[][] neighborArray, int[][] weight){ 52 for(int i=0; i<dataArray.length; i++){ 53 Vertex<T> myVertex = new Vertex<T>(dataArray[i]); 54 55 if(!verList.contains(myVertex)) { 56 for (int j = 0; j < neighborArray[i].length; j++) { 57 weightNeighbor newNeighbor = new weightNeighbor(neighborArray[i][j]); 58 newNeighbor.setWeight(weight[i][j]); 59 myVertex.addNeighbor(newNeighbor); 60 } 61 verList.add(myVertex); 62 } 63 } 64 } 65 66 //遍历图 67 void traverse(){ 68 for(int i=0; i<verList.size(); i++){ 69 Vertex<T> myVer = verList.get(i); 70 System.out.print("The graph Vertex data is "+ myVer.data + ","); 71 System.out.print("its neighbors are → "); 72 73 for(int j=0; j<myVer.neighbors.size(); j++) { 74 System.out.print(myVer.neighbors.get(j).index + "→"); 75 } 76 System.out.println(""); 77 } 78 } 79 80 //返回图的邻接链表 81 ArrayList<Vertex<T>> getVerList(){ 82 return verList; 83 } 84 85 } 86 87 // 图节点 88 class Vertex<T>{ 89 T data; 90 ArrayList<Neighbor> neighbors; 91 92 Vertex(T data){ 93 this.data = data; 94 neighbors = new ArrayList<Neighbor>(); 95 } 96 97 // 添加邻居数据 98 public void addNeighbor(Neighbor newNeighbor){ 99 if((newNeighbor!=null)&&(!neighbors.contains(newNeighbor))) 100 neighbors.add(newNeighbor); 101 } 102 103 public boolean equals(Object other){ //需要重写,ArrayList检查的时候需要用到 104 if((other!=null)&&(other instanceof Vertex)){ 105 Vertex another = (Vertex<T>) other; 106 return data.equals(another.data); 107 } 108 return false; 109 } 110 } 111 112 // 邻接链表节点,如果存储的是索引,在图发生变化的时候对应关系就改变了 113 class Neighbor{ 114 protected int index; 115 116 Neighbor(int index){ 117 this.index = index; 118 } 119 120 public boolean equals(Object other){ //需要重写,ArrayList检查的时候需要用到 121 if((other!=null)&&(other instanceof Neighbor)){ 122 Neighbor another = (Neighbor) other; 123 return index == another.index; 124 } 125 return false; 126 } 127 } 128 129 class weightNeighbor extends Neighbor{ 130 int weight; 131 132 weightNeighbor(int index){ 133 super(index); 134 } 135 136 void setWeight(int weight){ 137 this.weight = weight; 138 } 139 } 140 141 class GraphViolationException extends RuntimeException{ 142 GraphViolationException(String info){ 143 super(info); 144 } 145 }
经测试,运行情况良好!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号