huffman coding
继上一节树和二叉树的介绍,本文详细介绍一种特殊的二叉树,叫huffman tree(赫夫曼树)。如果读者是初学者的话,请思考几个问题。
为什么需要这样一种二叉树?这种数据结构有什么优点?如何实现?应用实例?
huffman coding
大家都知道huffman树,却很少提到huffman编码,但huffman编码是介绍huffman树绕不过的一道坎。
首先,说说编码的事。就像谍战片中常出现的编解码问题,没份电报通过编码加密之后发出去,收到电报的一份用约定好的解码规则将电报内容还原,这不仅是一种信息的传递方式,还有传递安全的重要意义。抛开安全不说,回到最初的编码问题。那么人们对编码最初的要求有哪些?
- 译码结果唯一,无歧义
- 编码后的电文尽可能短
就ABCD编码而言,你可能会想到编码成0、00、1、01,虽然编码是短了,但译码结果却不唯一了,比如“0000”就可以译为“AAAA”、“BB”、“AAB”、“BAA”、“ABA”多种电文,显然这种编码是不合格的。能保证任意字符的编码都不是其他字符编码的前缀的编码,就叫作前缀编码。
借助二叉树编码,如何确保译码结果唯一?
如果非叶子节点保存字符信息的话,那么就会出现歧义的现象。相反地,只要保证只在叶子节点上存储字符信息,就可以避免这种现象。
定义叶子的编码对应规则:从根节点出发,选择左子树代表编码0,右子树编码1,那么从根节点到叶子的过程中进行的一系列选择唯一对应了叶子的编码。还是以ABCD编码为例说明,图如下:
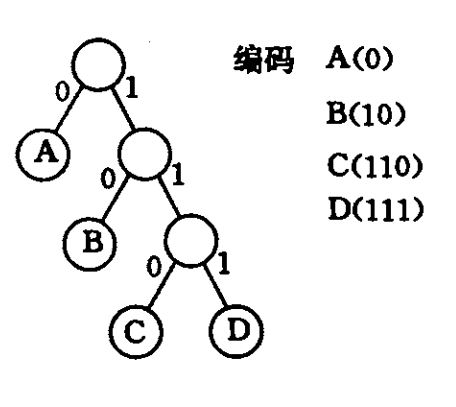
借助二叉树编码,如何使得电文最短?
在满足条件一的情况下,考虑电文最短问题。不同字符出现的概率不同,电文最短问题,就是在保证为前缀编码的前提下,使得出现频率越高的字符对应的编码越短。假设字符出现的概率为wi,其对应的叶子节点到根的路径长度为li,则求min∑wili ,也叫作带权路径长度。
huffman树就是这样一种数据结构,可以满足以上要求。即概率越大的字符叶子离节点越近,且为前缀编码。为何满足从其构造过程可见一斑。构造过程如下:
- 构造两个队列A和B,分别存放叶子节点和子树。
- 选择A和B中概率最小的两个节点m和n
- 构造一个新的二叉树o,新子树的概率为m和n的概率之和,m和n为其左右子树
- 将o加入B中,判断是否满足A为空且B中只有一颗子树,若不满足返回步骤2,满足进入步骤5
- 返回B中唯一的一颗子树作为huffman树
由其构造过程可知,huffman树是严格二叉树,也即其节点只有两个孩子或者没有孩子。又忍不住问两个问题:
为什么huffman树得是严格二叉树?
假如存在只有一个子节点的节点,那么该节点的子节点取代其之后,∑wili比之前更小,这样的树不满足电文最短的要求。
huffman树唯一吗?
可能不唯一,举个例子。
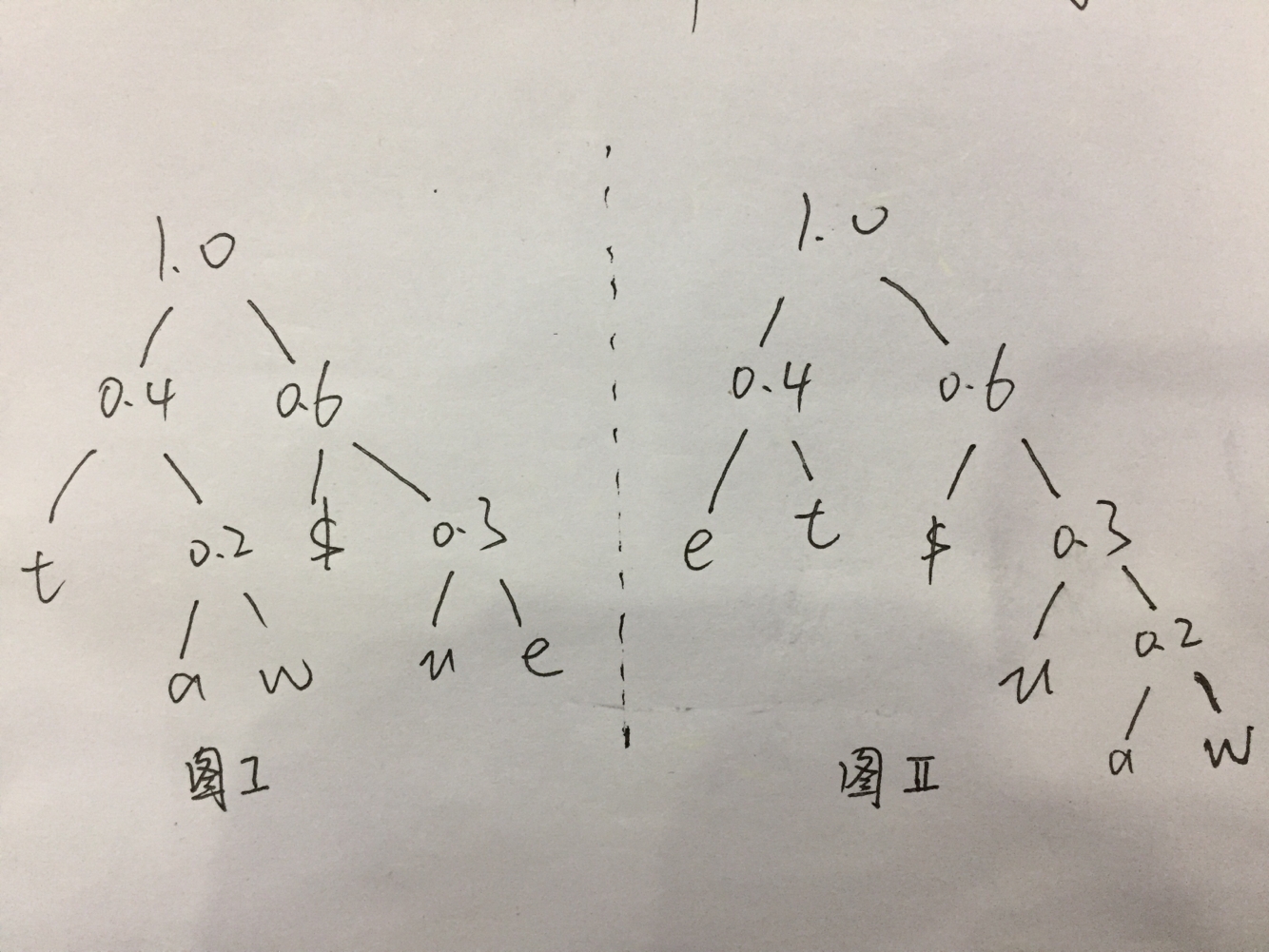
图I 和 图II 为相同字符集的不同huffman树结构,可以证明,它们的带权路径长度∑wili相同。
huffman coding 实现
好吧,说到这里也该给出huffman coding的实现代码了,鄙人不才,代码是自己实现的,大部分接口是《数据结构从应用到实现(JAVA)版》中设计。给出代码之前,说明几点:
- 类中设置了七个变量,symbols[] probs[]为输入变量,存放字符集和对应的概率,要注意输入的字符集要按出现的概率大小升序排列。
- locations存放与输入字符索引一一对应的叶子节点的引用,编码的时候特别有用不需要遍历整个树匹配字符了。
- leaves和trees为存放叶子节点和子树的队列。leaves和trees使用的队列结构,小编电脑里只实现过循环队列,所以偷了个懒,哈哈。为什么是队列?leaves里的叶子节点自然是按照概率升序排列,只会减少不会增加,可以保证队头元素概率最小。那trees呢?因为新增的子树是由本轮两个队列概率最小的节点构成,其肯定比前轮的子树构成节点概率大,所以trees里保存的子树概率也是升序排列,也即队头子树概率最小。
- 输出变量是huffman和codes,分别是构建好的huffman树 和 与输入字符索引一一对应的字符编码,codes作用和locations相同,是locations的生成物,使用其编码比locations更方便。
- huffman 中叶子保存的是symbols[]里字符的索引,类型为float,非叶子节点保存的是其概率数值。
- 其实,可以不用这么麻烦,直接定制节点数据结构就能解决,但这么编写代码无疑耦合性较低。
1 package com.structures.tree; 2 3 import com.structures.linear.CircularQueue; 4 5 import java.util.ArrayList; 6 7 /** 8 * Created by wx on 2017/11/4. 9 * Implement huffman encode and decode function. 10 */ 11 public class Huffman { 12 // input variables 13 private char[] symbols; 14 private float[] probs; 15 16 // process variables 17 private ArrayList<BinaryTree<Float>> locations; // Save the pointer of binary node. Array is okay,too. 18 private CircularQueue<BinaryTree<Float>> leaves; 19 private CircularQueue<BinaryTree<Float>> subTrees; 20 21 // output variables 22 private BinaryTree<Float> huffmanTree; 23 private String[] codes; // It is not necessary but useful when encode. 24 25 // initializer of huffman tree 26 public Huffman(char[] symbols, float[] probs){ 27 this.symbols = symbols; 28 this.probs = probs; 29 leaves = new CircularQueue<BinaryTree<Float>>(symbols.length); 30 subTrees = new CircularQueue<BinaryTree<Float>>(symbols.length/2 + 1); 31 locations = new ArrayList<BinaryTree<Float>>(); 32 codes = new String[symbols.length]; 33 34 if(symbols.length==0) 35 throw new TreeViolationException("Error input parameters!"); 36 else if(symbols.length==1){ // If there are only one node, use it as root. 37 buildLeaves(); 38 huffmanTree = leaves.dequeue(); 39 storeCodes(); 40 return; 41 } 42 43 buildLeaves(); 44 buildAll(); 45 huffmanTree = subTrees.dequeue(); 46 storeCodes(); 47 } 48 49 // create binary tree for each input char with its index 50 private void buildLeaves(){ 51 for(int i=0; i<symbols.length; i++){ 52 BinaryTree<Float> leaf = new BinaryTree<Float>(); 53 leaf.makeRoot((float)i); // The binary tree saves the index of char 54 leaves.enqueue(leaf); 55 locations.add(leaf); 56 } 57 } 58 59 // create a new binary tree with input trees 60 private BinaryTree<Float> buildTree(BinaryTree<Float> first, BinaryTree<Float> second){ 61 BinaryTree<Float> newTree = new BinaryTree<Float>(); 62 newTree.makeRoot(getProb(first)+getProb(second)); 63 newTree.attachLeft(first); 64 newTree.attachRight(second); 65 66 return newTree; 67 } 68 69 // return the tree's prob 70 private float getProb(BinaryTree<Float> tree){ 71 if(tree.left==null && tree.right==null) 72 return probs[(int)((float)tree.getData())]; 73 else 74 return tree.getData(); 75 } 76 77 // get the trees with the lowest probability. 78 // Caution! Only queue of leaves is not empty need this operation. 79 private BinaryTree<Float> getMin(){ 80 BinaryTree<Float> first = leaves.first(); 81 BinaryTree<Float> second; 82 83 if(subTrees.isEmpty()){ 84 return leaves.dequeue(); 85 }else{ 86 second = subTrees.first(); 87 if(getProb(first) > getProb(second)) 88 return subTrees.dequeue(); 89 else 90 return leaves.dequeue(); 91 } 92 } 93 94 // create the whole huffman tree 95 private void buildAll(){ 96 // Stage one 97 while(!leaves.isEmpty()){ 98 BinaryTree<Float> first = getMin(); 99 BinaryTree<Float> second; 100 if(!leaves.isEmpty()) 101 second = getMin(); 102 else 103 second = subTrees.dequeue(); 104 subTrees.enqueue(buildTree(first, second)); 105 } 106 // Stage two 107 while (subTrees.size()>1){ 108 subTrees.enqueue(buildTree(subTrees.dequeue(), subTrees.dequeue())); 109 } 110 } 111 112 // return the height of this tree 113 private int treeHeight(BinaryTree<Float> tree){ 114 if(tree==null) 115 return -1; 116 else 117 return Math.max(treeHeight(tree.left), treeHeight(tree.right)) + 1 ; 118 } 119 120 // store each codes of total chars 121 private void storeCodes(){ 122 char[] codeString = new char[treeHeight(huffmanTree)]; 123 124 // judge whether symbols.length equals 1 125 if(symbols.length==1) { 126 codes[0] = "0"; 127 return; 128 } 129 130 for(int i=0; i<symbols.length; i++){ 131 BinaryTree<Float> node = locations.get(i); 132 int index = treeHeight(huffmanTree)-1; 133 134 while(node.parent!=null){ 135 if(node.parent.left==node) 136 codeString[index] = '0'; 137 // codeString[index] = ((Integer) 0).toString().charAt(0); 138 else 139 codeString[index] = '1'; 140 index--; 141 node = node.parent; 142 } 143 codes[i] = new String(codeString, index+1, codeString.length-1-index); 144 // int codeLen =treeHeight(huffmanTree)-1-index; 145 // char[] newArray = new char[codeLen]; 146 // System.arraycopy(codeString, 0, newArray, 0, codeLen); 147 // codes[i] = newArray.toString(); 148 } 149 } 150 151 // encode the input String 152 public String encode(String originalString){ 153 int len = originalString.length(); 154 StringBuffer encodedString = new StringBuffer(); 155 156 for(int i=0; i<len; i++){ // encode char in order 157 char origin = originalString.charAt(i); 158 159 for(int j=symbols.length-1; j >= 0; j--){ 160 if(symbols[j]==origin){ 161 encodedString.append(codes[j]); 162 break; 163 } 164 } 165 } 166 return encodedString.toString(); 167 } 168 169 // decode the input String 170 public String decode(String encodedCode){ 171 StringBuffer originalString = new StringBuffer(); 172 int pointer = 0; 173 174 while(pointer<encodedCode.length()){ // Go through input code 175 BinaryTree<Float> node = huffmanTree; 176 177 while(node.left!=null && node.right!=null) { // Match the sub code 178 char code = encodedCode.charAt(pointer); 179 if (code == '0') 180 node = node.left; 181 else 182 node = node.right; 183 pointer++; 184 } 185 float fIndex = node.getData(); 186 int index = (int)fIndex; 187 originalString.append(symbols[index]); 188 } 189 190 return originalString.toString(); 191 } 192 }
经测试,表现良好!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号