VDN、QMIX、QTRAN、COMA

VDN、QMIX、QTRAN、COMA

论文名称：

VDN：《Value-Decomposition Networks For Cooperative Multi-Agent Learning》

QMIX: 《QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning》

QTRAN：《QTRAN: Learning to Factorize with Transformation for Cooperative Multi-Agent Reinforcement Learning》

COMA：《Counterfactual multi-agent policy gradients》

一、基本问题

这几篇论文都是为了解决多智能体强化学习的信度分配问题而提出的。

  • 信度分配问题

    信度分配问题用百度到的话来说是指如何合理地将任务、资源或信任分配给各个智能体。但是在这几篇论文中，由于多智能体合作环境下，智能体的奖励由智能体的联合动作决定，如何有效的衡量每一个智能体对团队贡献的大小就比较关键。

    举一个具体的例子来说：在有三个智能体的环境中，其中两个智能体做出了比较好的动作，而剩下一个智能体的动作比较差。此时环境依旧会给出较大的奖励。这个时候动作比较差的智能体就会认为较差的动作也可以得到较高的奖励，久而久之，就摆烂了（因为有其他两个智能体兜底）。

这几篇论文的关系可以用下面的脑图来表示。

img

图中可以看到，QMIX是VDN的改进，QTRAN是QMIX的改进。VDAC就是把AC中的Critic换成了QMIX。其中VDN、QMIX、QTRAN是基于值（DQN）得方法。COMA是基于策略（AC）得方法。

二、基础知识

  • 单智能体强化学习基础算法

    DQN、AC（Actor Critic），A2C。这里不过多介绍。

  • DRQN算法

    DRQN是在DQN的基础上加入了LSTM或者GRU等RNN组件。目的是为了使得智能体在不完全观测马尔可夫环境（POMDP）中可以有一定的记忆效应，从而更好的适应环境的特点。在多智能体环境中，很多时候智能体只能观察的自己的局部状态，这种环境就是典型的POMDP。

    在加入了RNN的算法中，训练的方式有所不同。主要在于轨迹信息的保存和采样上面。

    以DQN为例，DQN使用了经验回放技术（Reply Buffer）。该技术将智能体的轨迹信息保存在经验池中，通常我们会保存的轨迹的信息为： \(<s_t,a_t,r_t,s_{t+1}, done_t>\)。每次训练时，从池中随机采样一批数据进行训练。

    但是在加入的RNN组件后，由于一个回合前后的数据互相关联，此时如果使用随机采样，就破坏了一个回合之间轨迹的关联信息。所有加入了RNN的强化学习算法如果需要使用验回放技术，通常使用一整条回合的轨迹信息作为采样单位。举例来说，假设经验池的大小为10，那么经验池中最多会保存10个回合的轨迹信息（不是10步的信息）

    这个时候有两种采样方式：

    1. Bootstrapped Sequential Updates

      假设采样大小为5，每次冲经验池中随机采样5个回合的数据。按照步长最长回合进行对齐（回合步长不够的需要填充），如何进行训练。但是这种方式违背了独立同分布原则，因为如果一个回合的步长太长，网络将会输入大量前后关联的数据。但是DRQN论文中指出，这种方式实际训练效果还不错。

    2. Bootstrapped Random Updates

      为了经可能的避免输入大量前后相关的数据，可以在采样的回合数据中再随机选择一小段固定步长的片段。举例来说，先采样5个回合的数据，再在这5个回合的数据中，随机选择步长为32的片段，使用这些片段作为输入数据进行训练。

    DRQN论文中指出：关于采样方式1和2，理论上是2更好，但是实际的实验表明2并没有比1好多少。QMIX这些论文使用的也都是采样方式1。

  • 多智能体CTDE架构

    CTDE（centralized training and decentralized execution）中文名叫做集中式训练，分布式执行。该方式，通过一个全局的Critic网络评估每一个智能体动作或者状态的价值。在这个架构下，智能体只能观察到自己得局部状态，而不知道全局得状态，间接导致了信度分配问题。

三、QMIX、VDN、QTRAN

  • 个人全局最大条件（IGM条件）

    这个条件由QTRAN的论文提出，是对QMIX和VDN这一系列工作（没有COMA）研究问题的总结。IGM条件认为：

    每一个智能体的局部最优动作联合起来也是全局最优联合动作

    VDN、QMIX、QTRAN这三篇论文就是通过一系列的方法（约束条件）使得智能体的动作满足IGM条件。简单来说，就是要使得所有智能体做出最优动作的时候，收到的反馈最大。但是由于全局的奖励是无法修改的，所以这三篇论文的思路基本修改全局Q值。

3.1 VDN算法

VDN的思想最简单。把所有智能体动作的局部Q值，相加得到的Q值作为全局Q值。也就是：

\[Q_{total} = \sum_i^{n}Q(o_t^i,a^i_t) \tag{1} \]

其中 \(n\) 是智能体数量, \(o_t\) 表示 \(t\) 时刻智能体的局部观测。

然后对于每一个智能体，修改损失函数为：

\[\mathcal{L} = \sum_t^T\sum^n_i(Q_{total} - (r_t + \gamma Q(o^i_t,a^i_t)))^2 \tag{2} \]

这里的 \(T\) 是最大的步长。

这样，之后所有的智能体做出了局部最优的动作， \(Q_{total}\) 才能达到最大值，满足了IGM条件。

但是VDN论文中指出，VDN本质上是假设 \(Q(u,s_t) = Q_{total}\)。其中 \(u\) 是智能体联合动作， \(s_t\) 是全局状态。但是实际上这个等号是不成立的，但是架不住这样就是效果好。

3.2 QMIX

QMIX是VDN的改进。QMIX认为VDN的假设 \(Q(u,s_t) = Q_{total}\)不成立的原因在于，VDN直接把Q值线性相加，太简单粗暴了。如果用一个万能的神经网络来拟合 \(Q_{total}\) 就不能说\(Q(u,s_t) \neq Q_{total}\)了。

所以QMIX的结构如下：

img

图中有几点需要注意：

  1. QMIX网络的输入除了正常的局部观察 \(o_t\) 之外，还输入了智能体的上一步动作 \(u_{t-1}\)

  2. QMIX实际上使用了超网络非线性组合最终的 \(Q_{tol}(\tau, u)\), 这里的 \(\tau\) 表示的是轨迹，超网络的输入是全局的状态 \(s_t\)。使用超网络的原因论文中有解释。

  3. 由于使用了神经网络，一个很关键的问题如何保证这个超网络训练出来的结果一定满足IGM条件。所以QMIX对这个网络进行了约束：超网络必须单调递增。用论文中的公式表示就是：

    \[\dfrac{\partial Q_{tot}}{\partial Q_a} \geq 0, \forall a \in A \tag{3} \]

    具体到实现就是使得超网络所有参数必须大于0（对所有生成的参数取绝对值）。

    这样只有输入最大的局部Q值，超网络才会输出最大的全局Q值。

  4. 一个小细节，超网络 \(W_1\) 到 \(W_2\) 的激活函数是 ELU函数，超网络的激活函数（如果有）是 ReLU

3.3 QTRAN

QTRAN认为QMIX做出的约束（网络必须单调）还是太严格了而进一步放宽了约束条件。QTRAN的约束条件用一句话说，就是使得局部Q值最大的联合动作对应的联合Q值最大，其他的Q值是多少，单不单调不管，只要不超过最优的联合动作Q值就可以。

用论文中的公式总结就是：

\[\sum_{i=1}^{N}Q_{i}(\tau_{i},u_{i})-Q_{\mathrm{jt}}(\tau,u)+V_{\mathrm{jt}}(\tau)=\left\{ \begin{array}{l l} {{0}}&{{u=\bar{u}}}\\ {\geq 0} &{{u\not=\bar{u}}} \end{array}\right. \tag{4} \]

其中 \(Q_{jt}(\tau,u)\) 就是QMIX中的 \(Q_{tot}(\tau,u)\)。 \(V_{jt}(\tau)\) 是作者添加的修正项，定义为。

\[V_{jt}(\tau) = \mathop{max} \limits_{u} Q_{jt}(\tau, u) - \sum_i^NQ_i(\tau_i,\bar{u_i}) \tag{5} \]

QTRAN的整体结构如下：

img

图中有几点需要注意：

  1. 这张图里面很多参数是共享的，拟合 \(Q_{jt}(\tau,u)\)和 \(V_{jt}(\tau)\) 都使用了一个网络。
  2. 接1，实际上QTRAN过于复杂，有资料还表明QTRAN的效果还不如QMIX，所以QTRAN更多的是理论上的成果。
  3. 接2，图中的QTRAN-alt是作者也认为QTRAN（图中的QTRAN-base）太复杂了，所以提出了一个简化的版本。但是这里不展开。
  4. 接2和3，QTRAN的损失函数由三部分组成，分别是图中的 \(\mathcal{L}_{opt},\mathcal{L}_{nopt},\mathcal{L}_{td}\)。这三个损失函数也分别对应公式（4）的两种情况和公式（2）。具体可以阅读原论文。

四、COMA

COMA和前面三个不一样，是基于策略的方法，所以也没有IGM条件这样说法。COMA的思想在于，虽然环境给出的奖励是不能改变的，但是可以为奖励建立一个额外的模型，修正每一个智能体获得奖励。用论文中的公式来说就是：

\[D^a = r(s,u) - r(s, (u^{-a}, c^a))\tag{6} \]

这里 \(D^a\) 指的是智能体在全局状态 \(s\) 下做出动作 \(a\) 的修正后的奖励。 \(r(s,u)\) 是环境默认的奖励。 \(r(s,(u^(-a),c^a))\)是奖励的模型，其中 \(c^a\) 是一个默认的奖励。也就是说，对每一个状态的奖励减去一个默认动作的奖励就可以衡量智能体动作的好坏。所以问题就变成了如何知道默认的奖励。

论文中指出，可以手动选择一个动作但是不现实，实际上可以通过修改优势函数来间接达到公式（6）的效果。所以COMA提出了反事实基线，它修改优势函数为：

\[A^a(s,u) = Q(s,u) - \sum_{u'^a}\pi^a(u'^a|\tau^a)Q(s,(u^{-a},u'^a)) \tag{7} \]

公式（7）把A2C中的baseline修改为在其他智能体动作不变的情况下，智能体可以做的动作的Q值乘上对应的概率的和（这里可以和单个智能体的V值很像）。

最终COMA的结构如下：

img

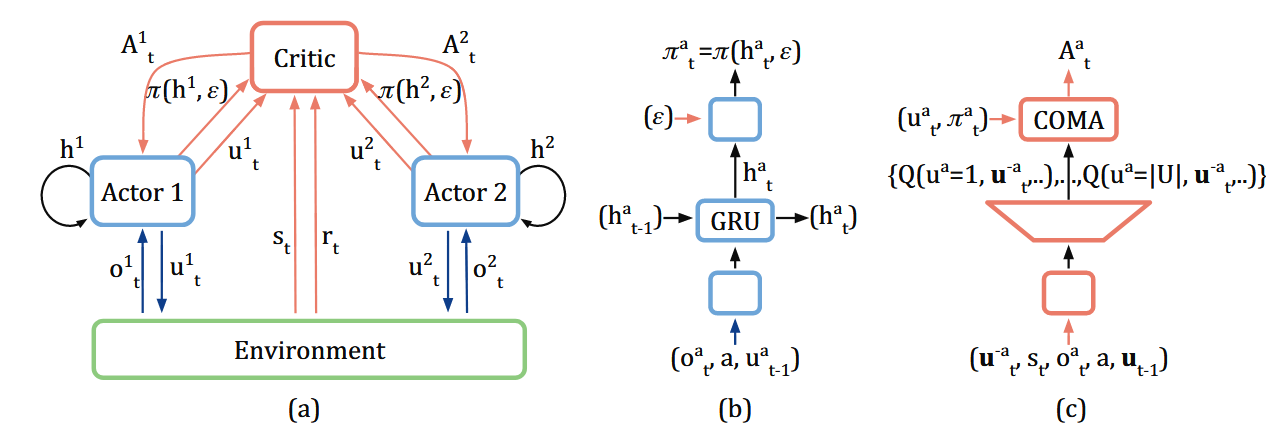
图中由几点需要注意：

  1. 图中(b)对应的是 Actor, (c)对应的是 Critic
  2. Actor中最后一层加入的一个超参数 \(\epsilon\)，这是 \(\epsilon\)-贪婪策略。在Softmax输出概率output后，修正动作概率为 \((1-\epsilon) * output + \epsilon\frac{1}{|U|}\) 其中 \(|U|\) 是可执行的动作数量
  3. Critic输入的是全局的状态和局部的状态、全局的联合动作，全局的上一步联合动作，Actor只输入局部的状态和局部的动作以及上一步的局部动作
  4. Critic的输出是一个智能体可以执行的所有动作的Q值，图中的COMA是计算优势函数的部分，严格来见不属于Critic
  5. 实际在实现的时候，在同构环境下，所有的Actor共享一套参数，只是会加入智能体的ID作为区分。
posted @ 2025-02-20 20:26  nagimegesa  阅读(722)  评论(0)    收藏  举报