JAVA PTA 大作业1
前言
PTA 上的JAVA大作业 前两次我认为是以熟悉JAVA语法为主,比较简单。从第三次开始必须要有一定的设计, 是以训练和考察面向对象的思想为主, 同时也涉及到一些JAVA为面向对象提供的C语言没有的特殊语法。
所以这里主要以分析第三次作业为主。
分析
第二次作业看一下第二题
第二题是这样的
RS232是串口常用的通信协议,在异步通信模式下,串口可以一次发送58位数据,收发双方之间没有数据发送时线路维持高电平,相当于接收方持续收到数据“1”(称为空闲位),发送方有数据发送时,会在有效数据(58位,具体位数由通信双方提前设置)前加上1位起始位“0”,在有效数据之后加上1位可选的奇偶校验位和1位结束位“1”。请编写程序,模拟串口接收处理程序,注:假定有效数据是8位,奇偶校验位采用奇校验。
输入格式:
由0、1组成的二进制数据流。例如:11110111010111111001001101111111011111111101111
输出格式:
过滤掉空闲、起始、结束以及奇偶校验位之后的数据,数据之前加上序号和英文冒号。
如有多个数据,每个数据单独一行显示。
若数据不足11位或者输入数据全1没有起始位,则输出"null data"。
若某个数据的结束符不为1,则输出“validate error”。
若某个数据奇偶校验错误,则输出“parity check error”。
若数据结束符和奇偶校验均不合格,输出“validate error”。
如:11011或11111111111111111。
例如:
1:11101011
2:01001101
3:validate error
这个题目不是很难, 直接看源码
import java.util.Locale;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String flow = sc.nextLine();
// 先检查整体格式的正确性
if(check(flow) || flow.length() < 11) {
System.out.println("null data");
return;
}
int cnt = 1;
for(int i = 0;i < flow.length() - 10; ++i) {
if(flow.charAt(i) != '0') continue;
// 检查数据结束符
if(flow.charAt(i + 10) == '0') {
System.out.println(cnt + ":validate error");
i += 10;
++cnt;
continue;
}
// 奇偶校验
// 先统计1的个数
int oneCnt = 0;
boolean isParity = false;
for(int j = i + 1; j < i + 9; ++j) {
if(flow.charAt(j) == '1') ++oneCnt;
}
// 判断奇偶校验是否正确
if(oneCnt % 2 == 0) {
isParity = flow.charAt(i + 9) == '0';
} else {
isParity = flow.charAt(i + 9) == '1';
}
if(isParity) {
System.out.println(cnt + ":parity check error");
} else {
System.out.println(cnt + ":" + flow.substring(i + 1, i + 9));
}
++cnt;
i += 10;
}
}
// 检查所有的数据是否都是0
private static boolean check(String s) {
for (int i = 0; i < s.length(); i++) {
if(s.charAt(i) == '0') return false;
}
return true;
}
}
第三次作业总共有三题。再分析之前我们先看看这三题目是什么。
-
第一题
输入连个点的坐标,计算两点之间的距离
输入格式:
4个double类型的实数,两个点的x,y坐标,依次是x1、y1、x2、y2,两个点的坐标之间以空格分隔,每个点的x,y坐标以英文 “,”分隔。例如:0,0 1,1或0.1,-0.3 +3.5,15.6。
若输入格式非法,输出"Wrong Format"。
若输入格式合法但坐标点的数量超过两个,输出“wrong number of points”。输出格式
计算所得的两点之间的距离。例如:1.4142135623730951
-
第二题
用户输入一组选项和数据,进行与直线有关的计算。选项包括:
1:输入两点坐标,计算斜率,若线条垂直于X轴,输出"Slope does not exist"。
2:输入三个点坐标,输出第一个点与另外两点连线的垂直距离。
3:输入三个点坐标,判断三个点是否在一条线上,输出true或者false。
4:输入四个点坐标,判断前两个点所构成的直线与后两点构成的直线是否平行,输出true或者false.
5:输入四个点坐标,计算输出前两个点所构成的直线与后两点构成的直线的交点坐标,x、y坐标之间以英文分隔",",并输出交叉点是否在两条线段之内(不含四个端点)的判断结果(true/false),判断结果与坐标之间以一个英文空格分隔。若两条线平行,没有交叉点,则输出"is parallel lines,have no intersection point"。输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。
例如:1:0,0 1,1
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
不论哪个选项,如果格式、点数量都符合要求,但构成任一条线的两个点坐标重合,输出"points coincide" -
第三题
用户输入一组选项和数据,进行与三角形有关的计算。选项包括:
1:输入三个点坐标,判断是否是等腰三角形、等边三角形,判断结果输出true/false,两个结果之间以一个英文空格符分隔。
2:输入三个点坐标,输出周长、面积、重心坐标,三个参数之间以一个英文空格分隔,坐标之间以英文","分隔。
3:输入三个点坐标,输出是钝角、直角还是锐角三角形,依次输出三个判断结果(true/false),以一个英文空格分隔,
4:输入五个点坐标,输出前两个点所在的直线与三个点所构成的三角形相交的交点数量,如果交点有两个,则按面积大小依次输出三角形被直线分割成两部分的面积。若直线与三角形一条线重合,输出"The point is on the edge of the triangle"
5:输入四个点坐标,输出第一个是否在后三个点所构成的三角形的内部(输出in the triangle/outof the triangle)。
必须使用射线法,原理:由第一个点往任一方向做一射线,射线与三角形的边的交点(不含点本身)数量如果为1,则在三角形内部。如果交点有两个或0个,则在三角形之外。若点在三角形的某条边上,输出"on the triangle"输入格式
同上
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
如果输入的三个点无法构成三角形,输出"data error"。
注意:输出的数据若小数点后超过6位,只保留小数点后6位,多余部分采用四舍五入规则进到最低位。小数点后若不足6位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333333,1.0按格式输出为1.0
选项4中所输入线的两个点坐标重合,输出"points coincide"
看完以上的三题我们可以发现一些联系
- 每一题的输入都有点, 并且要求检查点的合法性, 其中输入的点的格式都是一样的, 第二题和第三题这再驶入点之前增加了一个选项。
- 每一题的输出, 除非是正常输出, 如果遇见格式错误, 或者点重合都是输出相同的内容, 比如 "Wrong Format" 和 "points coincide"
- 题目中间是递进的, 比如第一题写点, 第二题写线, 第三题写三角形。而线由点组成, 三角形由点和线构成。根据已知的消息, 后面的题目是四边形和五边形, 也是可以由点线构成, 甚至和三角形有一定的联系。
根据以上三点, 再结合面向对象的思想。我们很自然的可以想到: 只要把点写好, 线使用点的部分直接调用点的模块, 由此把线写好, 三角形涉及到点和线的部分直接调用点和线的模块, 以后的四边形五边形也是如此,就可以省下很大的精力。
具体到面向对象就是要求我们要创建 点类, 线类, 三角形类。并且, 由于这三题有统一的输入格式, 我们可以创建一个输入类, 进行统一的输入。
设计
通过以上的分析, 我们可以开始进行设计。
-
点类
一个点, 最基本的的就是就是x,y坐标, 毫无疑问这个类的属性就是x 和 y。 由于第一问需要求点和点中间的距离所以点类有一个方法为求点和点的距离。得到类图如下。

-
线类
通常情况下, 两点确定一线。我们很自然的想到可以在线类中保存两个点。有这两点计算出各种其他的属性, 比如斜率。但是考虑到题目的要求, 我认为还是保存直线的坐标方程更加方便。直线的方程有一般式Ax + By + C = 0也有点斜式y = kx + c, 这里采用后者。考虑到没有斜率的情况, 应该在类中添加一个属性记录没有斜率的情况。再根据题目的要求, 我们需要再线中添加的方法有:- 求点线距离
- 判断三点是否一线(点是否满足线方程)
- 判断平行(斜率是否相等)
- 求线和线之间的交点
- 根据x 或 y 坐标的到 y 或 x 坐标
- 判断点是否再线段上
由此我们得到类图如下

其中 isBetweenLinePoint 为求点是否在线段上方法, 因为我们没有初始构造线段的两个点, 所以设置为静态的。
-
三角形类
根据题目的要求, 我们需要在求三角形的周长, 面积。需要使用射线法判断点是否在三角形内。
结合后边可能需要使用四边形五边形。考虑使用一个多边形类, 三角形和以后的四边形, 五边形继承多边形类。多边形类中实现与多边形边数无关的算法。
在这里我认为多边形应该是有线组成, 所以我认为多边形和线是组合关系, 和点是聚集关系, 为了统一处理, 这里采用一个点和线的数组记录构成多边形的点和线, 由继承的子类传入构造的点边的数量。所以多边形类应设置为abstract。
多边形类实现的方法有:- 构造多边形, 同时进行点的合法性检查
- 判断点是否是多边形上的点
- 判断线是否是多边形上的线
- 获得多边形的周长
- 判断点是否在多边形的边上(不包括顶点)
- 获得每一条边的长度
- 计算多边形面积,(
这个方法应设为抽象方法,参考某大佬博客写出了任意多变形面积计算的方法, 类图就不修改了,手动狗头)
有了多边形类, 我们就可以设计三角形类, 三角形类需要的方法就有 - 判断是否为等腰三角形
- 判断是否为等边三角形
- 判断是否为钝角, 锐角, 直角三角形
- 获得三角形重心
- 把三角形用线分割
由此得到三角形, 与多边形类图类图
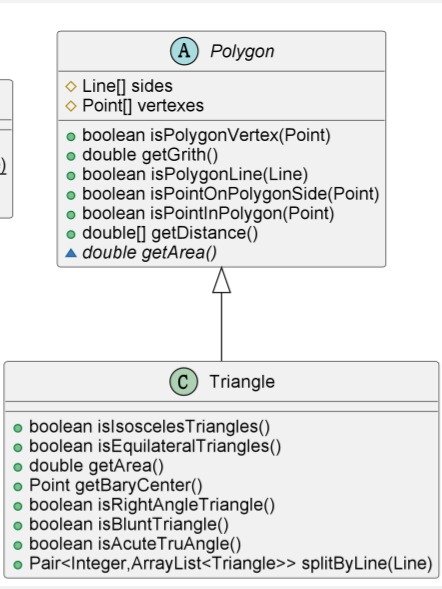
-
输入类
由题目的要求, 输入可以分成两个部分, 输入指令和输入点。于是输入类由两个方法, 分别输入指令和输入点。输入的方式可以模仿Scanner类, 扫描一个字符串, 提取出需要的部分并返回, 这个过程可以由Scanner完成。所以输入类的类图如下
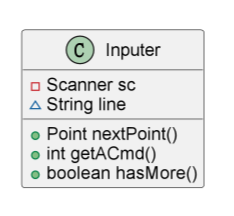
-
其他
-
Pair类
在三角形类的方法splitByLine 中要返回线与三角形交点个数与被分割成的三角形(也有考虑过将交点个数和分割三角形分开成为两个方法, 但是在割三角形的过程中自然的就得到了交点个数,并且考虑到切割的过程涉及到被切割的线与交点与顶点重合的情况,如果使用一个方法得到交点个数, 会丢失一定的信息反而不太方便, 所以干脆一起返回了)。由于JAVA中没有现成的比较方便的类似C++中pair的结构(Map.Entry是这样一个结构, 但是我并不是我想要的那样), 所以这里简单的添加一个Pair类, 类图如下

注意这里的Pair类是一个泛化的类, First和Second是泛化的两个对象。 -
Compare类
由于计算过程中会涉及到大量的浮点数比较, 而浮点数的存储具有不精确性, 所以浮点数一般情况下不能简单的进行比较。所以这里简单封装几个浮点数的比较方法, 在其他类中涉及比较统一调用这里的方法, 方便随时修改比较规则, 同时提高程序可读性。类图如下
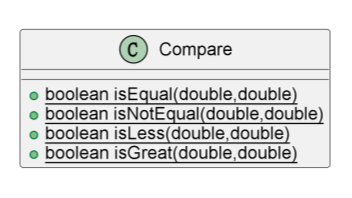
-
DoubleChanger类
第三题的输出由超过6为小数, 按四舍五入规则保留六位小数的要求。而小于六位小数则不能输出六位小数。因此简单封装一个DoubleChanger类转化浮点数为需要的类型。该类所需的方法也很简单, 只需要一个静态的转化方法。类图如下

-
实现
在将具体的实现前, 还有几点需要我们说明
-
关于错误的处理方式
阅读题目可以知道,测试样例中中有大量的错误样例。上课也讲过, 测试过程中有70%错误样例测试程序对错误输入的处理, 剩下30%是正确样例, 测试程序额运行结果。在这里每次遇到错误样例都必须中断程序, 然后输出对应的信息, 比如"Wrong Format"等信息。在C/C++中一般这种情况一般是采用状态码的方式,但是在JAVA中使用异常更加普遍。个人知道的一种常见的方法就是为每一种错误情况创建一个异常类(比如对于格式错误可以创建一个WrongFormatException类继承RuntimeException), 我们可以编写一个异常处理类, 利用多态统一的处理异常。但是我在实际实践的过程中, 发现为为每一个情况创建一个异常类过于繁琐。而且一开始没有规划好, 导致异常类的设置不太合理, 并且程序中充满了try .. catch结构, 看着非常难受。于是决定重写。
在重写过程中, 我发现了Exception类中有一个方法叫做getMessage可以获得抛出异常中返回的字符串。结合wrapper类的思想和题目的特征, 我想到可以把Main做为一个wrapper类调用实际的"Main", 在wrapper中使用一个try catch。异常统一采用RuntimeException, 但是在抛出过程中附带错误的类型,直接使用System.out.println(e.getMessage())打印错误信息,可以极大的简化程序流程。类似下面这个例子// file Main.java public class Main { public static void main(String arv[]) { RealMain realMain = new RealMain(); try { realMain.doSomething(); } catch (Exception e) { System.out.ptintln(e.getMessage()); } } } // file RealMain.java public class RealMain { void doSomething() { // ... do something if(...) { throw new RuntimeException("Wrong Format"); } // ... do some thing if(...) { throw new RuntimeException("points coincide"); } ... } }但是这样做相对于为每一错误创建一个异常类确实有缺点: 必须通过比较字符串才可以区分不同的错误。在必须需要捕获异常的时候就有点鸡肋了。但是从我写下来的事实来看, 这样的情况还是比较少的。所以我觉得这样做总体上来讲还是比前者方便的。
-
关于不同指令的不同函数调用方式。
正常情况下我们看到上面的23题有输入不同的选项调用不同的功能, 首先想到的一般是应该是switch case,我也是这样想的。但是在前面的第一点结构下, 我突然想到结合JAVA反射机制, 只要提前把需要调用的函数按一定规律命名, 一开始就输入一个指令, 使用反射调用的方法, 就在达到了switch case 的功能的同时还屏蔽了不同题目之间不同指令格式的差异。相当于一个动态变换的switch case结构。就像下面这样// file Main.java public class Main { public static void main(String arv[]) { Inputer inputer = new Inputer(); try { int cmd = inputer.getACmd(); // 通过反射调用 RealMain 的 "run" + cmd 方法 } catch (Exception e) { // 注意 这里处理异常的方式有所不同, 具体见下面源码 } } } // file RealMain.java public class RealMain { void run1() { // ... do something if(...) { throw new RuntimeException("Wrong Format"); } // ... do something } void run2() { // ... do something if(...) { throw new RuntimeException("points coincide"); } // ... do something } void run3() { // ... do something } ... }注意, 在这里main方法中的的catch大括号里面笼统的写了处理异常, 而不是 System.out.println(e.getMessage())是应为在反射中处理放射调用方法的异常有所不同, 并且这里有个特殊情况。具体见下面源码。
在这样的结构下, 只需要为每一个题目编写一个单独的"RealMain", 在RealMain中写好run1、run2...runN方法, 需要处理错误的时候就抛出一个RuntimeException携带错误信息, 个人认为十分方便。
既然上面干好讲完了Main函数的结构, 我们趁热打铁, 随便就把实际上的Main说明一下(注意因为第一问没有要求输入指令, 而且Main的功能相对简单, 就单独编写了一个Main, 所以下面的Main是为第二题以后的题目准备的)
// file Main.java
import java.lang.reflect.InvocationTargetException;
import java.util.Scanner;
public class Main {
// 这个是实际要调用的Main类的名字, 在这里写的TriangleMain是指第三题
static final String mainClass = "TriangleMain";
public static void main(String[] args) {
try {
// 首先创建一个Inputer 获得一个指令
Inputer inputer = new Inputer(new Scanner(System.in).nextLine());
int cmd = inputer.getACmd();
// 这里开始使用反射
// 创建 要调用的对象 在这里是 TriangleMain
Object o = Class.forName(mainClass)
.getDeclaredConstructor().newInstance();
// 获取要调用的方法并执行 注意这里传入了一个 inputer 参数
o.getClass().getDeclaredMethod(
"run" + cmd, Class.forName("Inputer"))
.invoke(o, inputer);
} catch (Exception e) {
// 使用反射调用的方法抛出的异常会被包装成 InvocationTargetException
// 在这里需要通过InvocationTargetException获得实际抛出的异常
if (e instanceof InvocationTargetException) {
Throwable exception =
((InvocationTargetException) e).InvocationTargetException();
System.out.println(exception.getMessage());
} else {
// 实际上 inputer类也可能抛出异常(见下面源码)
// 所以这里需要处理 inputer 抛出的异常
System.out.println(e.getMessage());
}
}
}
}
至于实际上Main 调用的 LineMain, 和 TriangleMain, 因为比较简单也没什么好分析的我们放到最后。
剩下的就是实现点、线、三角形类为主了。首先看点类.。
// file Point.java
public class Point {
private final double x;
private final double y;
/**
* Point 的构造函数, 通过传入x y 坐标构造一个点
* @param x x 坐标
* @param y y 坐标
*/
public Point(double x, double y) {
this.x = x;
this.y = y;
}
public double getX() {
return x;
}
public double getY() {
return y;
}
/**
* 求点和点之间的距离
* @param p 要求距离的另一个点
* @return 返回点和点之间的距离
*/
public double distanceTo(Point p) {
// 直接用坐标算出距离并返回
return Math.sqrt((p.x - x) * (p.x - x) + (p.y - y) * (p.y - y));
}
/**
* 比较两个点 x y 坐标相等就认为点相等
* @param b 传入的 点 因为 覆盖的关系必须是 Object
* @return 返回两个点是否相等的bool值
*/
@Override
public boolean equals(Object b) {
if (b instanceof Point p) {
return Compare.isEqual(p.x, x)
&& Compare.isEqual(p.y, y);
}
return false;
}
/**
* 覆盖的 toString 方法, 应为需要输出点, 所以特意覆盖这个方法
* @return 返回点的 字符串 形式
*/
@Override
public String toString() {
return x + "," + y;
}
}
然后是线类
// file Line.java
public class Line {
private final double k;
private final double c;
private final boolean isNoSlope;
/**
* Line 的构造函数 通过两个点构造一个线
* 在这里采用 y = kx + c 的形式
* 如果传入的 两个点相同 抛出异常 RuntimeException("points coincide");
* 如果线的斜率不存在则设置 isNoSlope为 true, 并且把 k 设置为 Double.MAX_VALUE
* @param x 传入的点 x
* @param y 传入的点 y
*/
public Line(Point x, Point y) {
if (x.equals(y)) throw new RuntimeException("points coincide");
if (Compare.isEqual(x.getX(), y.getX())) {
isNoSlope = true;
k = Double.MAX_VALUE;
c = x.getX();
} else {
// 计算 斜率 和 c
k = (x.getY() - y.getY()) / (x.getX() - y.getX());
c = y.getY() - k * y.getX();
isNoSlope = false;
}
}
/**
* 判断点是否在线段上(不含端点)
* 由于一开始 线类就没有保存最开始构造该线的两个点,
* 考虑到线段可以是线上的任意两个点, 因此该方法设置为静态的,
* 并需要传入两点构造一线, 再进行比较.
* 因为需要构造线, 所以有可能会抛出异常 RuntimeException("points coincide")。
* 若构造的线没有斜率, 则比较的是 y,否则比较 x
* @param x 构造线的一点 x
* @param y 构造线的一点 y
* @param p 需要判断是否在线段上的点
* @return 返回 p 是否在线段上, 注意, p 不在线上也是不在线段上
*/
public static boolean isBetweenLinePoint(Point x, Point y, Point p) {
Line l = new Line(x, y);
if (!l.isLinePoint(p)) return false;
double min;
double max;
if (l.isNoSlope()) {
min = Math.min(x.getY(), y.getY());
max = Math.max(x.getY(), y.getY());
boolean a = Compare.isLess(min, p.getY());
boolean b = Compare.isLess(p.getY(), max);
return a && b;
} else {
min = Math.min(x.getX(), y.getX());
max = Math.max(x.getX(), y.getX());
boolean a = Compare.isLess(min, p.getX());
boolean b = Compare.isLess(p.getX(), max);
return a && b;
}
}
/**
* 获得线的斜率
* 如果没有斜率抛出异常 RuntimeException("Slope does not exist");
* @return 返回斜率
*/
public double getSlope() {
if (isNoSlope()) throw new RuntimeException("Slope does not exist");
return k;
}
public double getC() {
return c;
}
public boolean isNoSlope() {
return isNoSlope;
}
/**
* 求点到线的距离
* 如果线的斜率不存在 则 使用 p.getX() - c
* 如果线的斜率存在 则使用公式 d = abs(x0 * k - y0 + C) / sqrt(k ^ 2 + 1)
* @param p 需要计算的点
* @return 返回点到线的距离
*/
public double distanceToPoint(Point p) {
if (isNoSlope()) {
return Math.abs(p.getX() - c);
}
double down = Math.sqrt(k * k + 1);
double up = Math.abs(k * p.getX() - p.getY() + c);
return up / down;
}
/**
* 判断点是否在线上
* 如果线的斜率不存在, 则比较 p的x坐标和c
* 如果线的斜率存在, 则看点是否满足线的公式 kx+c = y
* @param p 要判断的点
* @return 返回点是否在线上的bool值
*/
public boolean isLinePoint(Point p) {
if (isNoSlope()) return Compare.isEqual(p.getX(), c);
double y = k * p.getX() + c;
return Compare.isEqual(y, p.getY());
}
/**
* 判断两条线是否平行
* 主要通过比较斜率判断是否平行, 注意斜率不存在的情况
* 注意在这里两条相同的线会被认为是平行的
* @param l 要判断的线
* @return 返回是否平行的bool值
*/
public boolean isParallelLine(Line l) {
if (l.isNoSlope() && isNoSlope()) return true;
if (l.isNoSlope() || isNoSlope()) return false;
return Compare.isEqual(l.getSlope(), getSlope());
}
/**
* 通过 x 坐标获得 y 坐标
* 如果斜率不存在则 y 有无限个 抛出异常RuntimeException("Slope does not exist")
* @param x 传入的 x 坐标
* @return 返回 y 坐标
*/
public double getYByX(double x) {
if (isNoSlope()) throw new RuntimeException("Slope does not exist");
return k * x + c;
}
/**
* 通过 y 坐标获得 x 坐标
* @param y y 坐标
* @return 返回 x 坐标
*/
public double getXByY(double y) {
if (isNoSlope()) return c;
return (y - c) / k;
}
/**
* 计算两个线之间的交点
* 如果两条线平行, 抛出异常
* RuntimeException("is parallel lines,have no intersection point")
* 如果有其中一条线平行则根据线对应特征返回解
* 否则 根据 y = k1 * x + c1 以及 y = k2 * x + c2 联立解出 x y 返回对应的点
* @param l 需要相加的线
* @return 返回相交的点
*/
public Point intersectionPoint(Line l) {
if (isParallelLine(l))
throw new RuntimeException(
"is parallel lines,have no intersection point");
if (isNoSlope()) return new Point(c, l.getYByX(c));
if (l.isNoSlope()) return new Point(l.getC(), getYByX(l.getC()));
double x = (l.getC() - c) / (k - l.getSlope());
double y = (c * l.getSlope() - l.getC() * k) / (l.getSlope() - k);
return new Point(x, y);
}
/**
* 判断两条线是否相等, 主要是比较线的 k 和 c
* 注意, 即使线的斜率不存在 k(Double.MAX_VALUE) 和 c 也应该相等
* @param b 需要比较的线, 由于覆盖的原因是 Object
* @return 返回两条线是否相等的bool值
*/
@Override
public boolean equals(Object b) {
if (b instanceof Line l) {
return Compare.isEqual(c, l.c) && Compare.isEqual(k, l.k);
}
return false;
}
}
三角形类比较特殊需要继承多边形类
我们先看看多边形类
// file Polygon.java
public abstract class Polygon {
protected Line[] sides;
protected Point[] vertexes;
/**
* 多边形类的构造函数
* 在这里会假设每两个相邻的点 p 构成一条边
* 在当前情况下, 若有点重合会抛出异常RuntimeException("data error")
* @param p 传入多边形的点
* @param size 手动指定多边形的边数, 如果 size 于 p.length 不等 则抛出异常
* RuntimeException("polygon constructor error")
*/
public Polygon(Point[] p, int size) {
if(p.length != size)
throw new RuntimeException("polygon constructor error");
// 检查每一个点是否重合
for (int i = 0; i < p.length; ++i) {
for (int j = i + 1; j < p.length; ++j) {
if (p[i].equals(p[j]))
throw new RuntimeException("data error");
}
}
vertexes = p;
sides = new Line[size];
// 构造边
for (int i = 0; i < p.length; ++i) {
sides[i] = new Line(vertexes[i], vertexes[(i + 1) % p.length]);
}
}
/**
* 检查点是否为多边形顶点
* @param p 需要检查的点
* @return 返回点是否为多边形顶点的 bool 值
*/
public boolean isPolygonVertex(Point p) {
for (Point vertex : vertexes) {
if (p.equals(vertex))
return true;
}
return false;
}
/**
* 获取多变形的周长
* 这个方法在多边形类中实现是因为算法于多边形边数无关
* @return 返回多边形周长
*/
public double getGrith() {
double sum = 0;
// 循环相加多边形边长
for (int i = 0; i < vertexes.length; ++i) {
sum += vertexes[i]
.distanceTo(vertexes[(i + 1) % vertexes.length]);
}
return sum;
}
/**
* 判断线是否为多边形的边
* @param l 需要判断的边
* @return 返回 线是否是多边形边的 bool 值
*/
public boolean isPolygonLine(Line l) {
// 循环比较各个边
for (Line line : sides) {
if (line.equals(l))
return true;
}
return false;
}
/**
* 判断 点 是否在多变形的边上, 不包含多边形的顶点
* 该方法循环 调用 Line.isBetweenLinePoint 开销比较大, 少用
* @param p 传入的点
* @return 返回点是否在多边形上的 bool 值
*/
public boolean isPointOnPolygonSide(Point p) {
for (int i = 0; i < vertexes.length; ++i) {
if (Line.isBetweenLinePoint(vertexes[i]
, vertexes[(i + 1) % vertexes.length], p))
return true;
}
return false;
}
/**
* 判断点是否在多边形内
* 如果点在多边形上(在多边形边上, 或者是多边形顶点)
* 抛出异常RuntimeException("on the polygon")
* 否则采用射线法:
* 默认以传入点 p(x0,y0) 为一点, 以点 p1(x0 + 1, y0) 为另一点构造一线 l
* 计算 l 与多边形各边交点, 并统计交点 x 坐标大于 x0 的数量 c
* 若 c 为奇数则点一定在多边形内
* 若 c 为偶数则一定在多边形外
* 注意此方法和多边形的形状无关
* @param p 需要判断的点
* @return 返回 点p 是否在多边形内的 bool值
*/
public boolean isPointInPolygon(Point p) {
if (isPointOnPolygonSide(p) || isPolygonVertex(p))
throw new RuntimeException("on the polygon");
Point p1 = new Point(p.getX() + 1, p.getY());
Line l = new Line(p1, p);
int cnt = 0;
for (Line side : sides) {
try {
Point intersect = side.intersectionPoint(l);
if (Compare.isGreat(intersect.getX(), p.getX()))
if (isPointOnPolygonSide(intersect))
++cnt;
} catch (Exception ignore) {
}
}
return cnt % 2 != 0;
}
/**
* 获得多边形各个边的边长
* 该方法直接调用 Point.distanceTo(p1)获得各边边长
* @return 返回会各边边长数组
*/
public double[] getDistance() {
double[] d = new double[vertexes.length];
for (int i = 0; i < vertexes.length; ++i) {
d[i] = vertexes[i]
.distanceTo(vertexes[(i + 1) % vertexes.length]);
}
return d;
}
/**
* 求多边形面积
* 参考某大佬的博客, 虽然我是看不懂
* 这里附上链接 http://www.cnblogs.com/TenosDoIt/p/4047211.html
* @return 返回多边形面积
*/
public double getArea() {
int length = vertexes.length;
double area = vertexes[0].getY()
* (vertexes[length - 1].getX() - vertexes[1].getX());
for(int i = 1;i < vertexes.length; ++i) {
area += vertexes[i].getY()
* (vertexes[i - 1].getX() - vertexes[(i + 1) % length].getX());
}
return Math.abs(area / 2);
}
}
注意, 再多边形类的构造函数中, 我尝试使用一个统一的方法检查构造多边形点的合法性, 但是时间不太够, 所以还没有完成, 等到以后再完善。
以后到了。。 写后面的题目发现, 这里几乎不可能做到统一的检测, 由于我没有区分不同的异常, 而不同的题目要求无法构造输出的信息不一样, 所以这里只能做一般性的检测。针对不同的多边形还要在对应的构造函数里完成。并且在写代码的过程中发现了一个求任意多边形面积的方法, 虽然我不太看的懂, 但是这里还是感谢大佬, 附上链接http://www.cnblogs.com/TenosDoIt/p/4047211.html
然后是三角形
// file Triangle.java
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Objects;
public class Triangle extends Polygon {
public Triangle(Point[] p) {
super(p, 3);
}
/**
* 判断是否是等腰或等边三角形的辅助函数
* 这里计算出每两条边是否相等的 bool 值并返回数组
* @return 返回每两条边 是否相等的 bool 值数组
*/
private boolean[] disCompare() {
double[] distance = getDistance();
boolean a = Compare.isEqual(distance[0], distance[1]);
boolean b = Compare.isEqual(distance[0], distance[2]);
boolean c = Compare.isEqual(distance[1], distance[2]);
return new boolean[]{a, b, c};
}
/**
* 判断是否是等腰三角形
* 只要有两条边相等就是等腰三角形
* @return 返回是否是等腰三角形的 bool 值
*/
public boolean isIsoscelesTriangles() {
boolean[] res = disCompare();
return res[0] || res[1] || res[2];
}
/**
* 判断是否是等边三角形
* 所有的边相等就是等边三角形
* @return 返回是否是等边三角形的 bool 值
*/
public boolean isEquilateralTriangles() {
boolean[] res = disCompare();
return res[0] && res[1] && res[2];
}
/**
* 计算三角形面积
* 这里直接利用 底 乘 高 / 2
* @return 返回三角形面积
*/
@Override
public double getArea() {
double high = sides[0].distanceToPoint(vertexes[2]);
double low = vertexes[0].distanceTo(vertexes[1]);
return high * low / 2;
}
/**
* 获得三角形重心
* 三角形重心就是 ((x0 + x1 + x2) / 3, (y0 + y1 + y2) / 3)
* @return 返回三角形重心
*/
public Point getBaryCenter() {
double x = (vertexes[0].getX()
+ vertexes[1].getX() + vertexes[2].getX()) / 3;
double y = (vertexes[0].getY()
+ vertexes[1].getY() + vertexes[2].getY()) / 3;
return new Point(x, y);
}
/**
* 判断三角形是否是锐角, 直角, 钝角的辅助函数
* 这里计算出每一条边的平方, 然后利用勾股定理判断三角形类形
* 这里之所以直接算平方而不用 p.distance(p1) 是因为该方法使用了开方
* 再平方会有精度损失
* @return 返回各个边的平方数组
*/
private double[] powerOfDistance() {
double[] dis = new double[3];
for (int i = 0; i < 3; ++i) {
Point p1 = vertexes[i];
Point p2 = vertexes[(i + 1) % 3];
dis[i] = Math.pow(p1.getX() - p2.getX(), 2)
+ Math.pow(p1.getY() - p2.getY(), 2);
}
Arrays.sort(dis);
return dis;
}
/**
* 判断是否是直角三角形
* 若是直角三角形 则有 a ^ 2 + b ^ 2 = c ^ 2
* @return 返回是否是直角三角形的 bool 值
*/
public boolean isRightAngleTriangle() {
double[] dis = powerOfDistance();
return Compare.isEqual(dis[0] + dis[1], dis[2]);
}
/**
* 判断是否是钝角三角形
* 若是直角三角形 则有 a ^ 2 + b ^ 2 < c ^ 2
* @return 返回是否是钝角三角形的 bool 值
*/
public boolean isBluntTriangle() {
double[] dis = powerOfDistance();
return Compare.isLess(dis[0] + dis[1], dis[2]);
}
/**
* 判断是否是锐角三角形
* 若是直角三角形 则有 a ^ 2 + b ^ 2 > c ^ 2
* @return 返回是否是锐角三角形的 bool 值
*/
public boolean isAcuteTruAngle() {
double[] dis = powerOfDistance();
return Compare.isGreat(dis[0] + dis[1], dis[2]);
}
/**
* splitByLine 的辅助函数
* 该方法用线与三角形每一条线相交, 判断交点是否在三角形上
* 并返回交点与三角形对应的线
* @param l 需要相交的线
* @return 返回相交的点和线
*/
public Pair<ArrayList<Point>, ArrayList<Line>>
intersectByLine(Line l) {
ArrayList<Point> points = new ArrayList<>();
ArrayList<Line> lines = new ArrayList<>();
for (Line side : sides) {
try {
Point p = side.intersectionPoint(l);
if (isPointOnPolygonSide(p) || isPolygonVertex(p)) {
points.add(p);
lines.add(side);
}
} catch (Exception ignore) {
}
}
return new Pair<>(points, lines);
}
/**
* 用线切割三角形
* 如果 线是三角形的边则抛出异常
* RuntimeException("The point is on the edge of the triangle");
* 该方法尝试使用线切割三角形, 并返回线与三角形交点个数以及被且切成的三角形
* 交点个数有 0, 1, 2 三中情况
* 分别对应 0, 0, 1 或 2 个三角形具体分析见源码
* @param l 切割的线
* @return 返回交点个数和被切割而成的三角形
*/
public Pair<Integer, ArrayList<Triangle>> splitByLine(Line l) {
if (isPolygonLine(l))
throw new RuntimeException("The point is on the edge of the triangle");
ArrayList<Triangle> triangles = new ArrayList<>();
Pair<ArrayList<Point>, ArrayList<Line>>
arrayListArrayListPair = intersectByLine(l);
ArrayList<Point> points = arrayListArrayListPair.getFirst();
ArrayList<Line> lines = arrayListArrayListPair.getSecond();
// 如果每有交点
if (points.size() == 0)
return new Pair<>(0, triangles);
// 如果只有一个交点
if (points.size() == 1 ||
(points.size() == 2 && points.get(0).equals(points.get(1)))) {
return new Pair<>(1, triangles);
}
// 有两个交点
if (lines.size() == 2) {
Point[] t = new Point[]{points.get(0)
, points.get(1), lines.get(0).intersectionPoint(lines.get(1))
};
triangles.add(new Triangle(t));
} else { // 有两个交点但是有一个交点是三角形顶点
Point v = null;
Point other = null;
for (Point point : points) {
if (isPolygonVertex(point)) {
v = point;
} else
other = point;
}
for (int i = 0; i < 3; ++i) {
if (Objects.equals(v, vertexes[i])) {
assert v != null;
triangles.add(
new Triangle(new Point[]{
v, other, vertexes[(i + 1) % 3]}));
triangles.add(
new Triangle(new Point[]{
v, other, vertexes[(i + 2) % 3]}));
break;
}
}
}
return new Pair<>(2, triangles);
}
}
注意这里还是重写了三角形计算面积的方法, 没有使用Polygon中的方法。
最后一个比较重要的Inputer类
// file Inputer.java
import java.util.Scanner;
public class Inputer {
private final Scanner sc;
String line;
/**
* Inputer类的构造函数
* 这里使用一个Scanner来解析字符串, 返回输入的点和或者指令
* @param l 需要解析的串
*/
public Inputer(String l) {
this.line = l;
this.sc = new Scanner(line);
}
/**
* 获得下一个输入的点
* 如果不存在下一个点 抛出异常 RuntimeException("wrong number of points")
* 否则使用正则表达式进行检查, 如果不符合指定的格式, 抛出异常
* RuntimeException("Wrong Format")
* 如果检查全部通过就会返回一个新的点对象
* @return 下一个点
*/
public Point nextPoint() {
if (!sc.hasNext())
throw new RuntimeException("wrong number of points");
// 这里因为使用只使用一个正则表达式的化过于复杂, 所以拆开了一点一点检查
String s = sc.next();
// 基本格式的初步检查
if (!s.matches("^[+-]?\\d+(\\.\\d+)?,[+-]?\\d+(\\.\\d+)?$"))
throw new RuntimeException("Wrong Format");
// 分割两个坐标
String[] xy = s.split(",");
// 排除特殊情况
for (String t : xy) {
if (t.equals("0."))
throw new RuntimeException("Wrong Format");
String[] tmp = t.split("\\.");
if (!tmp[0].matches("[+-]?(0|[1-9][0-9]*)"))
throw new RuntimeException("Wrong Format");
if (tmp.length == 2) {
if (!tmp[1].matches("(0|[1-9][0-9]*)"))
throw new RuntimeException("Wrong Format");
}
}
return new Point(
Double.parseDouble(xy[0]),
Double.parseDouble(xy[1])
);
}
/**
* 获得一个指令
* 如果 line 不符合基本的格式抛出异常 RuntimeException("Wrong Format")
* @return 返回一个指令
*/
public int getACmd() {
if (!line.matches("^[1-5]:[+\\-.0-9,\\s]+"))
throw new RuntimeException("Wrong Format");
// 先要使用 : 为分隔符 后面需要跳过 :
sc.useDelimiter(":");
String s = sc.next();
sc.useDelimiter(" ");
sc.skip(":");
return Integer.parseInt(s);
}
/**
* 判断输入之后还有没有内容
* @return 返回有没有内容的 bool 值
*/
public boolean hasMore() {
return sc.hasNext();
}
}
最后是一些辅助类, 这里直接全部给出
// file Compare.java
public class Compare {
public static boolean isEqual(double a, double b) {
return a == b;
}
public static boolean isNotEqual(double a, double b) {
return a != b;
}
public static boolean isLess(double a, double b) {
return a < b;
}
public static boolean isGreat(double a, double b) {
return a > b;
}
}
// file DoubleChanger.java
import java.math.BigDecimal;
import java.math.RoundingMode;
public class DoubleChanger {
public static double valueOf(double d, int how) {
return new BigDecimal(d)
.setScale(how, RoundingMode.HALF_UP).doubleValue();
}
}
最后的最后还有Main类实际上调用的"Main", 应为这几个类实际上就再调用上面的类的方法然后输出结果,这里只附上LineMain(第二题的),其他的也就是这样
public class LineMain {
public void run1(Inputer inputer) {
Point x = inputer.nextPoint();
Point y = inputer.nextPoint();
if (inputer.hasMore()) {
throw new RuntimeException("wrong number of points");
}
Line l = new Line(x, y);
System.out.println(l.getSlope());
}
public void run2(Inputer inputer) {
Point p = inputer.nextPoint();
Point x = inputer.nextPoint();
Point y = inputer.nextPoint();
if (inputer.hasMore()) {
throw new RuntimeException("wrong number of points");
}
Line l = new Line(x, y);
System.out.println(l.distanceToPoint(p));
}
public void run3(Inputer inputer) {
Point p = inputer.nextPoint();
Point x = inputer.nextPoint();
Point y = inputer.nextPoint();
if (inputer.hasMore()) {
throw new RuntimeException("wrong number of points");
}
Line l = new Line(x, y);
System.out.println(l.isLinePoint(p));
}
public void run4(Inputer inputer) {
Point x0 = inputer.nextPoint();
Point y0 = inputer.nextPoint();
Point x1 = inputer.nextPoint();
Point y1 = inputer.nextPoint();
if (inputer.hasMore()) {
throw new RuntimeException("wrong number of points");
}
Line l1 = new Line(x0, y0);
Line l2 = new Line(x1, y1);
System.out.println(l1.isParallelLine(l2));
}
public void run5(Inputer inputer) {
Point x0 = inputer.nextPoint();
Point y0 = inputer.nextPoint();
Point x1 = inputer.nextPoint();
Point y1 = inputer.nextPoint();
if (inputer.hasMore()) {
throw new RuntimeException("wrong number of points");
}
Line l1 = new Line(x0, y0);
Line l2 = new Line(x1, y1);
Point p = l1.intersectionPoint(l2);
boolean res = true;
if (p.equals(x0) || p.equals(y0) || p.equals(x1) || p.equals(y1))
res = false;
else res = Line.isBetweenLinePoint(x0, y0, p) ||
Line.isBetweenLinePoint(x1, y1, p);
System.out.println(p + " " + res);
}
}
从上面的LineMain可以看到, 我们只需要在类中写好 run1 run2 run3 ... 等方法, 方法的内容也只是简单的调用 Line 类的方法, main 函数会自动的调用 run1 run2 等方法。
总结
这次大作业应该是为后面几次大作业打基础的一次, 所以也是十分重要的一次。只要这次的作业设计好了, 后边应该会轻松很多。也正是这样, 这次作业我重写了两次, 两次都是因为代码的结构不好, 越写越烦躁。最后就从新来了。关于怎么设计出一个很好的面向对象的程序我并不是特别懂,所以才会不断的重写。但是在这个过程中我觉得有一点很重要, 就是自己在写代码的过程中要有意识的"偷懒", 已经写过一遍的功能就不要再写第二遍。很直观的做法就是讲这些功能封装成函数, 也就是JAVA中的方法或者类。也正是基于这样的想法, 当我看到后面的四边形的题目的时候, 我就知道最开始三角形类应该要提取出来一个父类多边形。于是就开始重第二次重写。。。这也在一方面告诉我, 在考虑一个复杂的系统的时候, 必须要考虑长远, 虽然面向对象相对于面向过程, 特别是JAVA啰嗦了很多。但是一开始的基础写好了, 后面只会越来越方便。但是JAVA本身就没有C++灵活, 而且异常这个东西我用的还不是很熟练, 所以还是总体来讲还是踩了不少坑。
关于题目中的大量浮点运算, 有很多时候某个选项的部分样例通过了, 然后有一两个样例过不去。中央的问题困扰了很久。后来和同学不断的交流, 发现这大概率是计算精度的问题。修改的方法就是修改计算的方法。就比如第二题计算交点的样例中如果单纯的采用两个方程联立求解(也就是上面源码写的方法)精度是不够的。原因是上面的算法使用了大量的除法, 在乘回去的时候值就变了。所以这里应该尽量避免使用除法。再比如第三题求三角形是钝角锐角还是直角的过程中, 我一开始的想法是用余弦定理求出每个角然后和\(\frac \pi 2\)比较。后来发现精度严重不足。换成使用勾股定理, 一开始直接使用 p.distanceTo(p2) 获得边长后再平方虽然正确的点比之前多, 但是还是不够。最后才发现问题再开方于是直接中顶点重新开始算距离并且不开方。
最后看看SourceMonitor对源码的分析
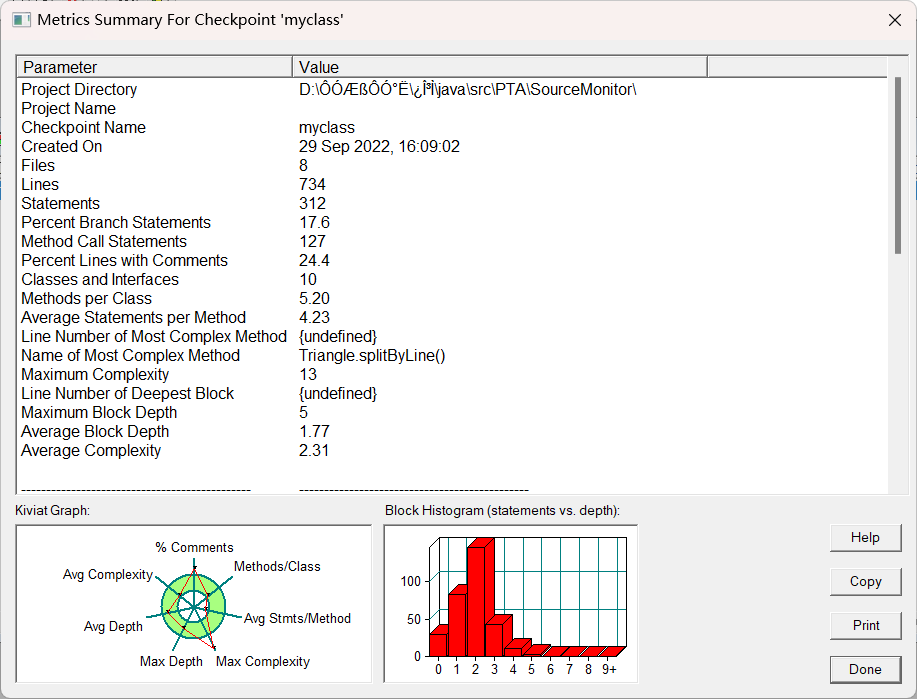
从结果上来看, 我的Triangle.splitByLine()方法的复杂度比较高, 高达13。但平均复杂度比较小。问题主要在Triangle.splitByLine()这个函数, 但是我还没想好怎么优化。然后是我的注释好像有点多。。平均的方法数比较少。这确实还是需要改进的地方。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号