代码随想录
复杂度、测试用例、边界条件
时间复杂度:看每一个元素被操作的次数
图解!24张图彻底弄懂九大常见数据结构!_业余码农AmazingJ的博客-CSDN博客_图解数据结构
void()仅仅是代表不返回任何值,但是括号内的表达式还是要运行,如
void(alert("Warnning!"))
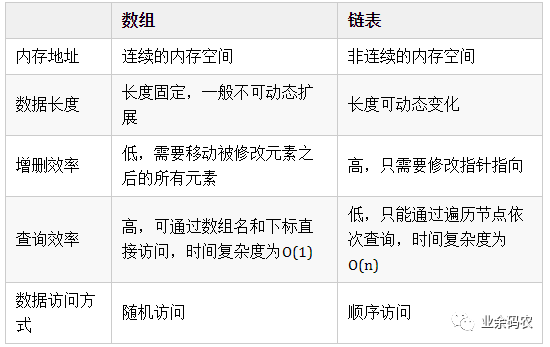
1 数组
理论:
数组的元素在内存地址中是连续的,不能单独删除数组中的某个元素,只能覆盖。
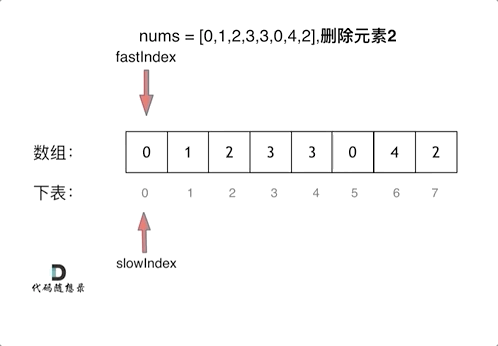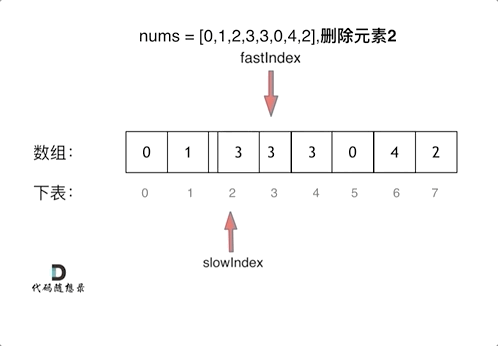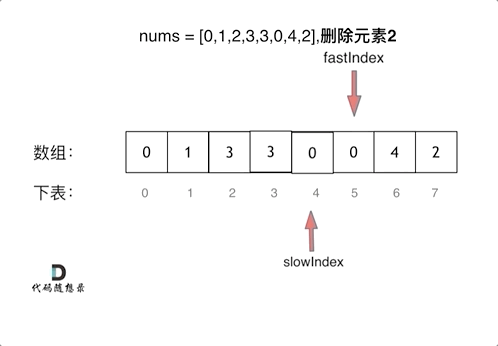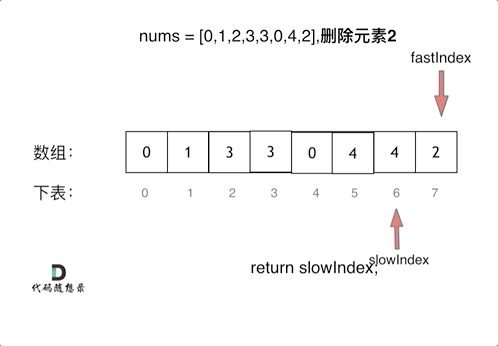
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
方法 双指针法
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
数组、链表、字符串常见使用双指针法。
思路
慢指针重新定义一个数组,快指针遍历原数组,若是目标元素,就不赋值给新数组,非目标元素,赋值
```javascript
var removeElement = function(nums, val) {
let k=0
for(let i=0;i<nums.length;i++){
if (nums[i]!= val){
nums[k++]=nums[i]
}
}
return k
};
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
方法 双指针法
思路

var sortedSquares = function(nums) {
let i=0
let j=nums.length-1
let k=nums.length-1
let res = new Array(nums.length-1).fill(0)
while(k>=0){
if(nums[i]*nums[i]<nums[j]*nums[j]){
res[k--]=nums[j]*nums[j]
j--
}else {
res[k--]=nums[i]*nums[i]
i++
}
}
return res
};
例3 长度最小的子数组
方法 滑动窗口
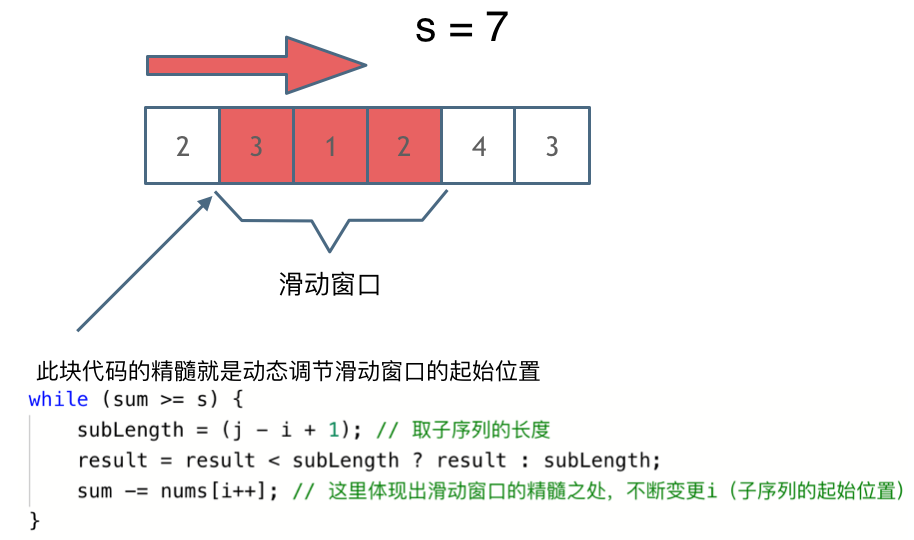
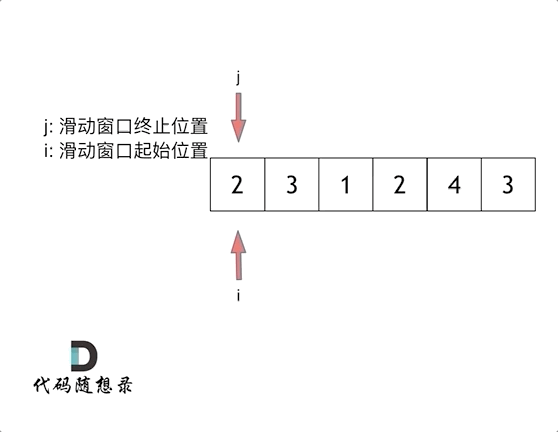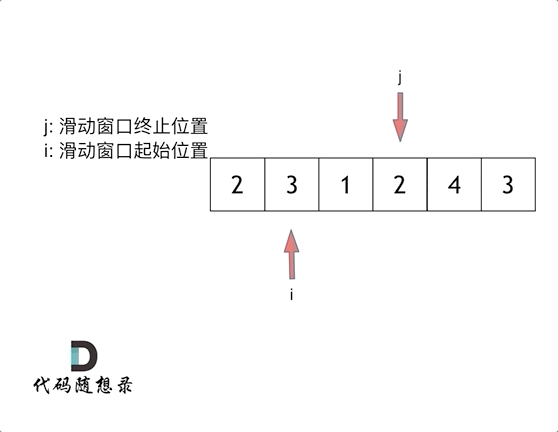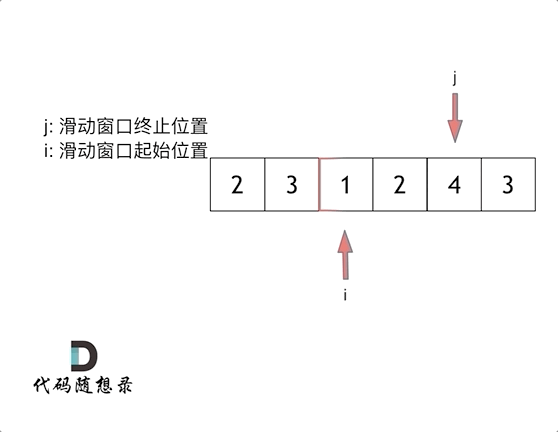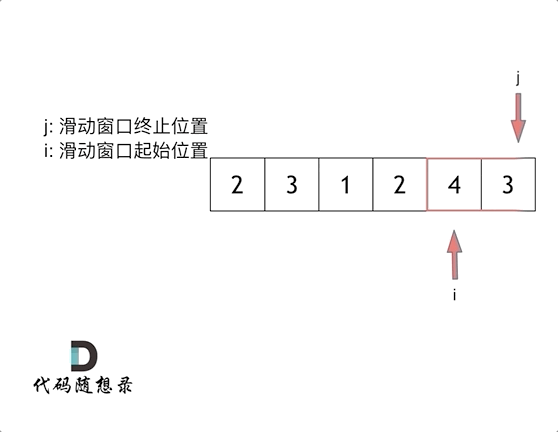
就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
思路
两个循环 第一个循环是右指针遍历数组,累加和;第二个循环是用来窗口滑动:确定和是否大于目标值,同时移动左指针,这里注意计算子数组的长度r-l(因为上一个循环r已经多加1)
var minSubArrayLen = function(target, nums) {
// 长度计算一次
const len = nums.length;
let l = r = sum = 0,
res = len + 1; // 子数组最大不会超过自身
while(r <= len-1) { //r=len时取不到
sum += nums[r++];
// 窗口滑动
while(sum >= target) {
// r始终为开区间 [l, r)
res = res < r - l ? res : r - l;
sum-=nums[l++];
}
}
return res > len ? 0 : res;
};
例4 螺旋矩阵Ⅱ
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
for (; col < n; col++) { } //在循环开始前已经设置了col值
思路:
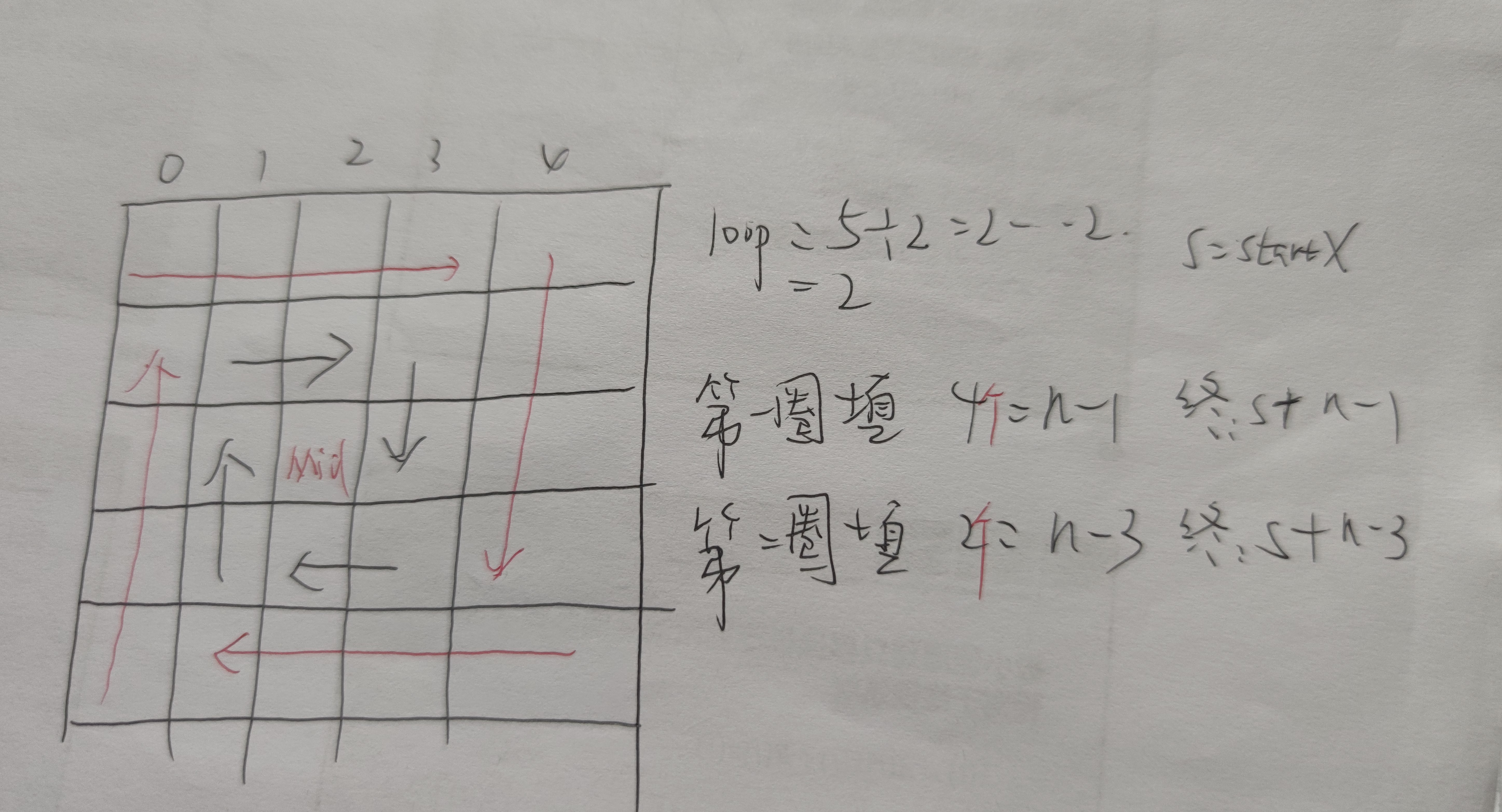
确定转多少圈(loop),每一圈遍历的起始位置startX (0,0)→(1,1)→(2,2)…,中间位置mid是为了当n为奇数时最后一个数,offset 用于表达每一次遍历的条件。循环是loop不断减一
var generateMatrix = function(n) {
let startX = startY = 0; // 起始位置
let loop = Math.floor(n/2); // 旋转圈数
let mid = Math.floor(n/2); // 中间位置
let offset = 1; // 控制每一层填充元素个数
let count = 1; // 更新填充数字
let res = new Array(n).fill(0).map(() => new Array(n).fill(0));
while (loop--) {
let row = startX, col = startY;
// 上行从左到右(左闭右开)
for (; col < startY + n - offset; col++) {
res[row][col] = count++;
}
// 右列从上到下(左闭右开)
for (; row < startX + n - offset; row++) {
res[row][col] = count++;
}
// 下行从右到左(左闭右开)
for (; col > startX; col--) {
res[row][col] = count++;
}
// 左列做下到上(左闭右开)
for (; row > startY; row--) {
res[row][col] = count++;
}
// 更新起始位置
startX++;
startY++;
// 更新offset
offset += 2;
}
// 如果n为奇数的话,需要单独给矩阵最中间的位置赋值
if (n % 2 === 1) {
res[mid][mid] = count;
}
return res;
};
定义
链表是一种通过指针串联在一起的线性结构,每一个节点由两部分组成,一个是数据域一个是指针域(存放指向下一个节点的指针),最后一个节点的指针域指向null(空指针的意思)。
链接的入口节点称为链表的头结点也就是head。
class ListNode {
val;
next = null;
constructor(value) {
this.val = value;
this.next = null;
}
}
分类
单链表
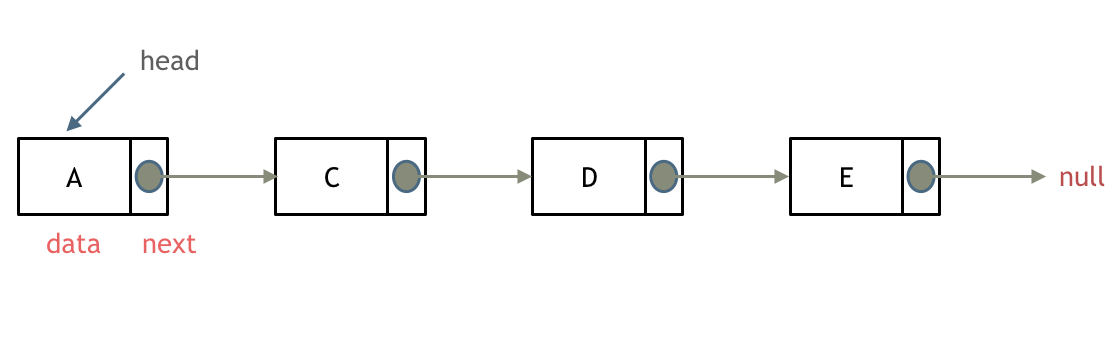
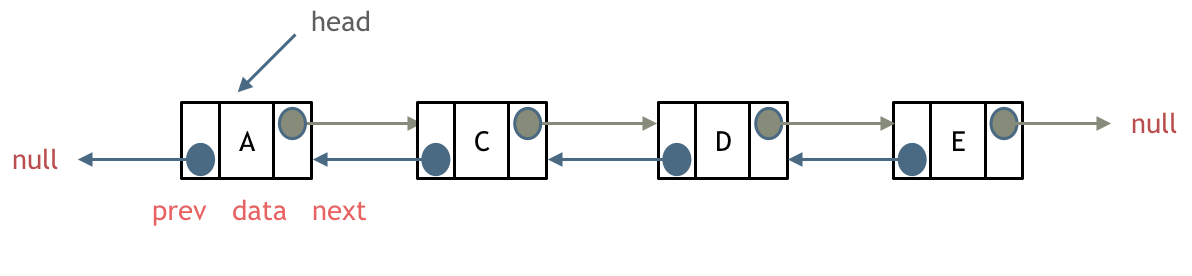
双链表:每一个节点有两个指针域,一个指向下一个节点,一个指向上一个节点。双链表 既可以向前查询也可以向后查询。
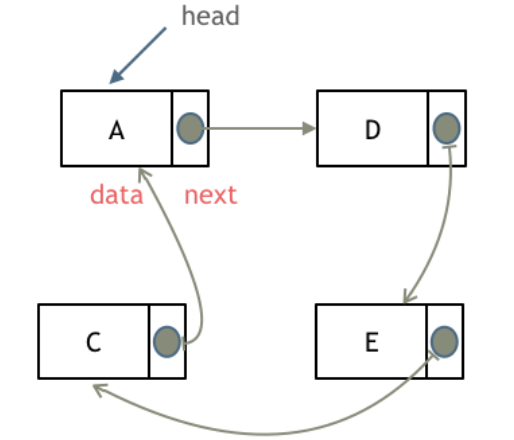
循环链表:链表首尾相连。解决约瑟夫环问题。
链表的存储方式
数组是在内存中是连续分布的,但是链表在内存中不是连续分布的。
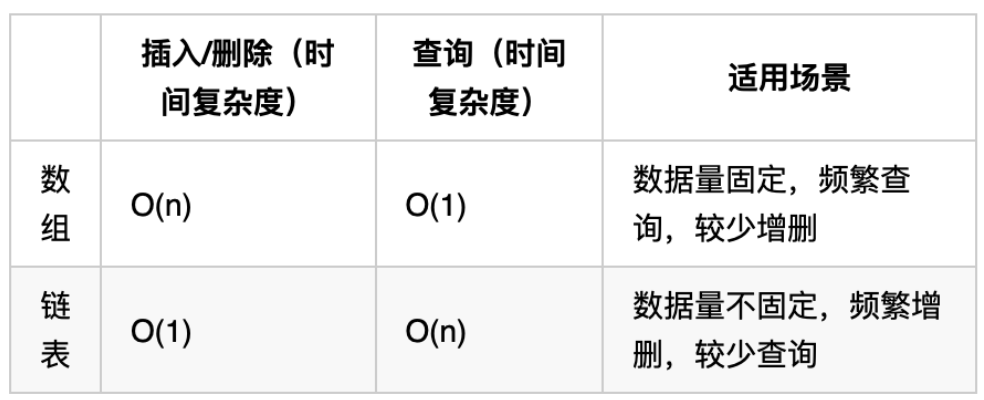
数组在定义的时候,长度就是固定的,如果想改动数组的长度,就需要重新定义一个新的数组。
链表的长度可以是不固定的,并且可以动态增删, 适合数据量不固定,频繁增删,较少查询的场景。
例1 移除链表元素
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
思路
设置一个虚拟节点ret,这样操作所有链表节点都会以同样的逻辑。再定义一个暂时节点cur遍历链表。
if: 判断当前节点下一个节点的数据值是否等于目标值,是的话,指针指向下一个的下一个。再返回循环中,判断下一个节点的数据值是否等于目标值,不等的话,cur遍历到下一个节点
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
var removeElements = function(head, val) {
let res=new ListNode(0,head)
let cur=res
while(cur.next){
if (cur.next.val==val){
cur.next=cur.next.next
continue
}
cur=cur.next
}
return res.next
};
例2 设计链表
设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性:val 和 next。val 是当前节点的值,next 是指向下一个节点的指针/引用。如果要使用双向链表,则还需要一个属性 prev 以指示链表中的上一个节点。假设链表中的所有节点都是 0-index 的。
在链表类中实现这些功能:
-
get(index):获取链表中第 index 个节点的值。如果索引无效,则返回-1。
-
addAtHead(val):在链表的第一个元素之前添加一个值为 val 的节点。插入后,新节点将成为链表的第一个节点。
-
addAtTail(val):将值为 val 的节点追加到链表的最后一个元素。
-
addAtIndex(index,val):在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度,则该节点将附加到链表的末尾。如果 index 大于链表长度,则不会插入节点。如果index小于0,则在头部插入节点。
-
deleteAtIndex(index):如果索引 index 有效,则删除链表中的第 index 个节点。
思路
考虑在链表的什么位置操作,注意头尾分情况考虑。size数量变化,最重要的是index考虑头尾节点的变化,操作该节点是否影响head、tail变化。注意在合适处加上return 否则报错
①先定义一个类LinkNode-链表 ②初始化数据结构(单链表储存头尾节点和节点数量)
Get函数:③定义原型方法 获得节点getNode (index在[0,size-1]之外,返回null;创建虚拟头节点cur,★利用while循环,index递减,使cur遍历到初始index处) ④ 返回利用getNode返回该index节点的val
addAtHead 函数 ⑤定义一个新节点node,分别重新定义head、size、tail,若tail不存在,说明原链表不存在,将node再赋值给tail
addAtTail 函数 ⑥ 定义一个新节点node,size++,判断tail是否存在(原链表是否为null),是()否(node赋值给头尾)
addAtIndex 函数 ⑦
-
-
index > this._size return
-
index <= 0 addAtHead
-
index === this._size addAtTail
-
-
0<index<size 利用getNode 获取目标节点的上一个节点node,定义一个新节点赋值给node.next
deleteAtIndex 函数 ⑧
-
index < 0 || index >= size
-
index === 0
-
index === this._size - 1 //如果删除的这个节点同时是尾节点,要处理尾节点
-
-
0<index<size 获取目标节点的上一个的节点
-
index === this._size - 1
-
class LinkNode {
constructor(val, next) {
this.val = val;
this.next = next;
}
}
var MyLinkedList = function() {
this._size=0
this._head=null
this._tail=null
};
MyLinkedList.prototype.getNode = function(index) {
if(index<0||index>=this._size) return null
let cur = new LinkNode(0,this._head)
while(index-- >=0){
cur=cur.next
}
return cur
};
MyLinkedList.prototype.get = function(index) {
if(index<0||index>=this._size) return -1
return this.getNode(index).val
};
MyLinkedList.prototype.addAtHead = function(val) {
let node = new LinkNode(val,this._head)
this._head = node
this._size++
if(!this._tail){
this._tail=node
}
};
MyLinkedList.prototype.addAtTail = function(val) {
let node = new LinkNode(val,null)
this._size++
if(this._tail){
this._tail.next=node
this._tail=node
return
}
this._tail=node
this._head=node
};
MyLinkedList.prototype.addAtIndex = function(index, val) {
if (index>this._size) return
if (index<=0){
this.addAtHead(val)
return
}
if(index==this._size){
this.addAtTail(val)