hiho图的联通性（自留）

无向图割边割点算法

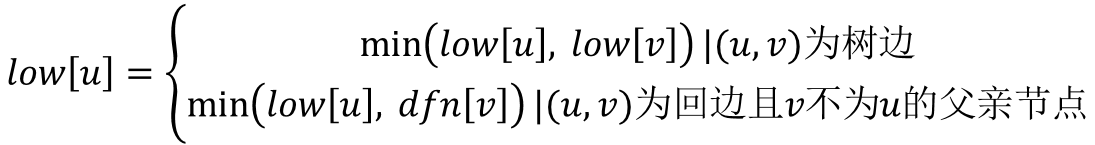
而当(u,v)为树边且low[v]>dfn[u]时，表示v节点只能通过该边(u,v)与u连通，那么(u,v)即为割边。

void dfs(int u) {
    //记录dfs遍历次序
    static int counter = 0;    
    
    //记录节点u的子树数
    int children = 0;
    
    ArcNode *p = graph[u].firstArc;
    visit[u] = 1;

    //初始化dfn与low
    dfn[u] = low[u] = ++counter;

    for(; p != NULL; p = p->next) {
        int v = p->adjvex;
        
        //节点v未被访问，则(u,v)为树边
        if(!visit[v]) {
            children++;
            parent[v] = u;
            dfs(v);

            low[u] = min(low[u], low[v]);

            //case (1)
            if(parent[u] == NIL && children > 1) {
                printf("articulation point: %d\n", u);
            }

            //case (2)
            if(parent[u] != NIL && low[v] >= dfn[u]) {
                printf("articulation point: %d\n", u);
            }
            
            //bridge
            if(low[v] > dfn[u]) {
                printf("bridge: %d %d\n", u, v);
            }
        }

        //节点v已访问，则(u,v)为回边
        else if(v != parent[u]) {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

 

边双联通分量算法

对于一个无向图的子图，当删除其中任意一个点后，不改变图内点的连通性，这样的子图叫做点的双连通子图。而当子图的边数达到最大时，叫做点的双连通分量。

直观的做法自然先用上周的算法求出所有桥，去掉所有桥之后再做DFS求出每一个连通子图。我们这周要介绍一种更"抽象"的算法，通过在Tarjan算法当中巧妙地用一个栈来统计出每一个组内的节点，其代码如下：

void dfs(int u) {
    //记录dfs遍历次序
    static int counter = 0;    
    
    //记录节点u的子树数
    int children = 0;
    
    ArcNode *p = graph[u].firstArc;
    visit[u] = 1;

    //初始化dfn与low
    dfn[u] = low[u] = ++counter;
    
    //将u加入栈
    stack[++top] = u;

    for(; p != NULL; p = p->next) {
        int v = p->adjvex;
        
        //节点v未被访问，则(u,v)为树边
        if(!visit[v]) {
            children++;
            parent[v] = u;
            dfs(v);

            low[u] = min(low[u], low[v]);
            if (low[v] > dfn[u]) {
                printf("bridge: %d %d\n", u, v);    // 该边是桥
                bridgeCnt++;  
            }
        }

        //节点v已访问，则(u,v)为回边
        else if(v != parent[u]) {
            low[u] = min(low[u], dfn[v]);
        }
    }
    
    if (low[u] == dfn[u])
    {
        // 因为low[u] == dfn[u]，对(parent[u],u)来说有dfn[u] > dfn[ parent[u] ]，因此low[u] > dfn[ parent[u] ]
        // 所以(parent[u],u)一定是一个桥，那么此时栈内在u之前入栈的点和u被该桥分割开
        // 则u和之后入栈的节点属于同一个组
        将从u到栈顶所有的元素标记为一个组，并弹出这些元素。
    }
}

 

强连通分量

对于有向图上的2个点a,b，若存在一条从a到b的路径，也存在一条从b到a的路径，那么称a,b是强连通的。
对于有向图上的一个子图，若子图内任意点对(a,b)都满足强连通，则称该子图为强连通子图。
非强连通图有向图的极大强连通子图，称为强连通分量。
特别地，和任何一个点都不强连通的单个点也是一个强连通分量。

tarjan(u)
{
    Dfn[u]=Low[u]=++Index                      // 为节点u设定次序编号和Low初值
    Stack.push(u)                              // 将节点u压入栈中
    for each (u, v) in E                       // 枚举每一条边
        if (v is not visted)                   // 如果节点v未被访问过
            tarjan(v)                          // 继续向下找
            Low[u] = min(Low[u], Low[v])
        else if (v in Stack)                   // 如果节点v还在栈内(很重要,无向图没有这一步)
            Low[u] = min(Low[u], Dfn[v])
    if (Dfn[u] == Low[u])                      // 如果节点u是强连通分量的根
        repeat
            v = Stack.pop                      // 将v退栈，为该强连通分量中一个顶点
            mark v                             // 标记v，同样通过栈来找连通分量
        until (u == v)
}

scc + 缩点 + topo

 

点的双连通分量

对于一个无向图的子图，当删除其中任意一个点后，不改变图内点的连通性，这样的子图叫做点的双连通子图。而当子图的边数达到最大时，叫做点的双连通分量。

                                       

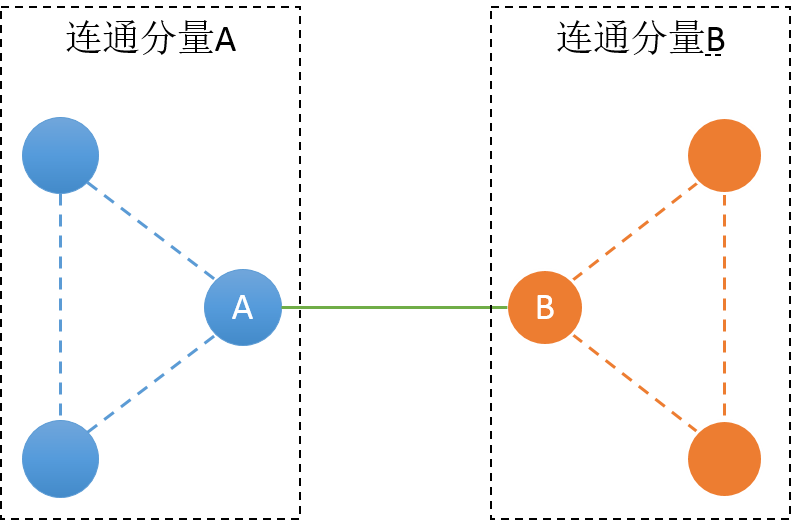
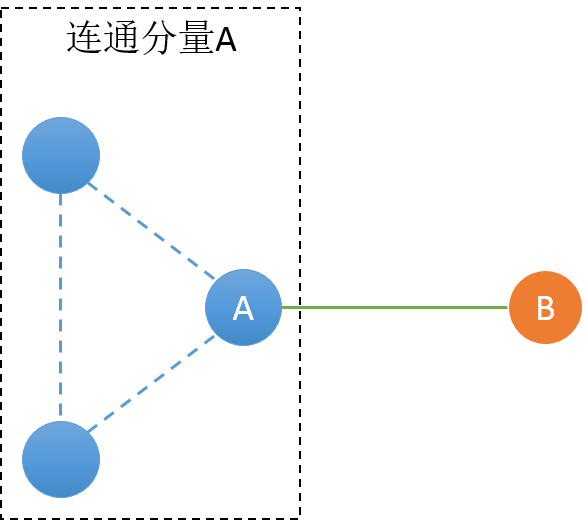
对于桥的两种情况，它分割个区域数刚好就等于割点数+1；而连通分量内的割点同样也是，每存在一个割点，点的双连通分量就增加一个。

点的双连通分量就等于割点数量加1。

每存在一个割点，就把一个区域一分为二，所以最后的结果也就是统计割点的数量就可以了。而对于分组具体情况，我们仍然采用栈来辅助我们记录

void dfs(int u) {
    //记录dfs遍历次序
    static int counter = 0;    
    
    //记录节点u的子树数
    int children = 0;
    
    ArcNode *p = graph[u].firstArc;
    visit[u] = 1;

    //初始化dfn与low
    dfn[u] = low[u] = ++counter;

    for(; p != NULL; p = p->next) {
        int v = p->adjvex;
        if(edge(u,v)已经被标记) continue; 

        //节点v未被访问，则(u,v)为树边
        if(!visit[v]) {
            children++;
            parent[v] = u;
            edgeStack[top++] = edge(u,v); // 将边入栈
            dfs(v);
            
            low[u] = min(low[u], low[v]);

            //case (1)
            if(parent[u] == NIL && children > 1) {
                printf("articulation point: %d\n", u);
                // mark edge
                // 将边出栈，直到当前边出栈为止，这些边标记为同一个组
                do {
                    nowEdge = edgeStack[top];
                    top--;
                    // 标记nowEdge
                }    while (nowEdge != edge(u,v))
            }

            //case (2)
            if(parent[u] != NIL && low[v] >= dfn[u]) {
                printf("articulation point: %d\n", u);
                // mark edge
                // 将边出栈，直到当前边出栈为止，这些边标记为同一个组
                do {
                    nowEdge = edgeStack[top];
                    top--;
                    // 标记nowEdge
                }    while (nowEdge != edge(u,v))
            }
            
        }

        //节点v已访问，则(u,v)为回边
        else if(v != parent[u]) {
            edgeStack[top++] = edge(u,v);
            low[u] = min(low[u], dfn[v]);
        }
    }
}