多分类及多标签分类算法
单标签二分类问题
单标签二分类算法原理
单标签二分类这种问题是我们最常见的算法问题,主要是指label标签的取值只有两种,并且算法中只有一个需要预测的label标签;直白来讲就是每个实例的可能类别只有两种(A or B);此时的分类算法其实是在构建一个分类线将数据划分为两个类别。常见的算法:Logistic、SVM、KNN、决策树等。
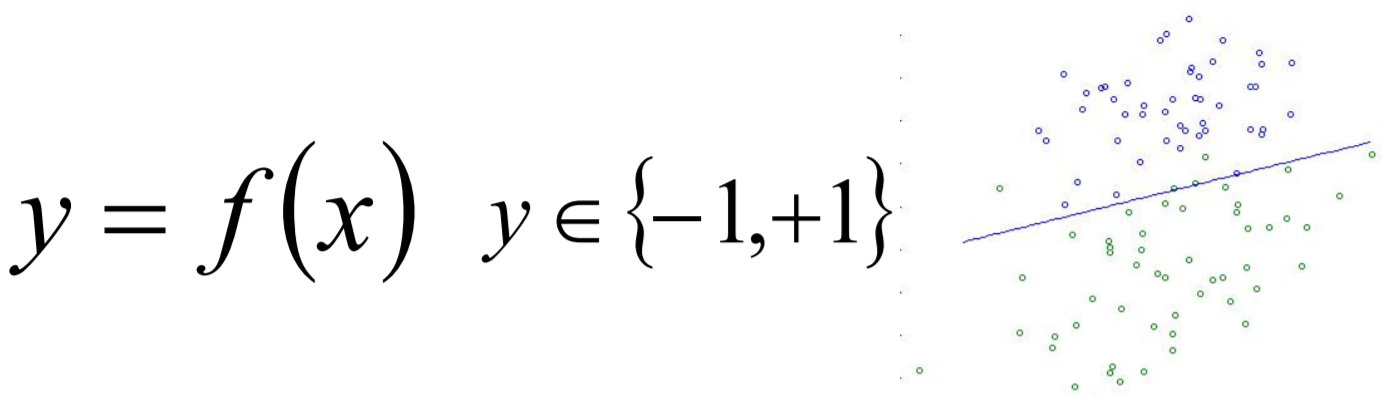
Logistic算法原理
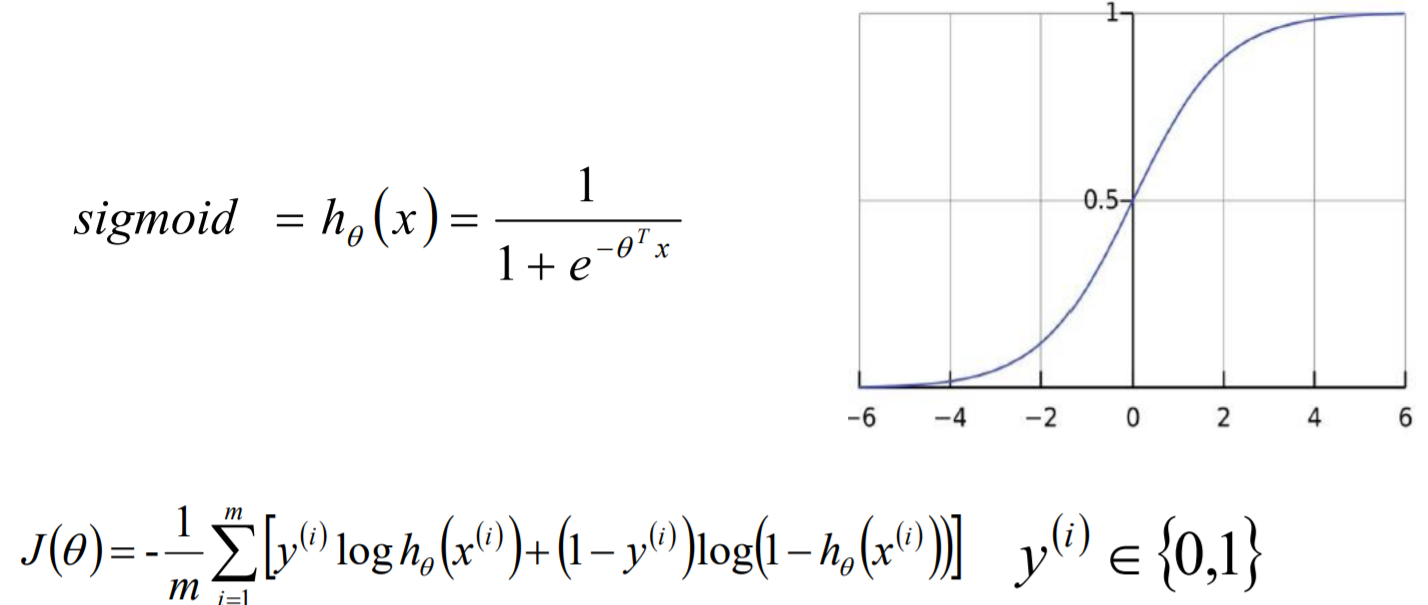
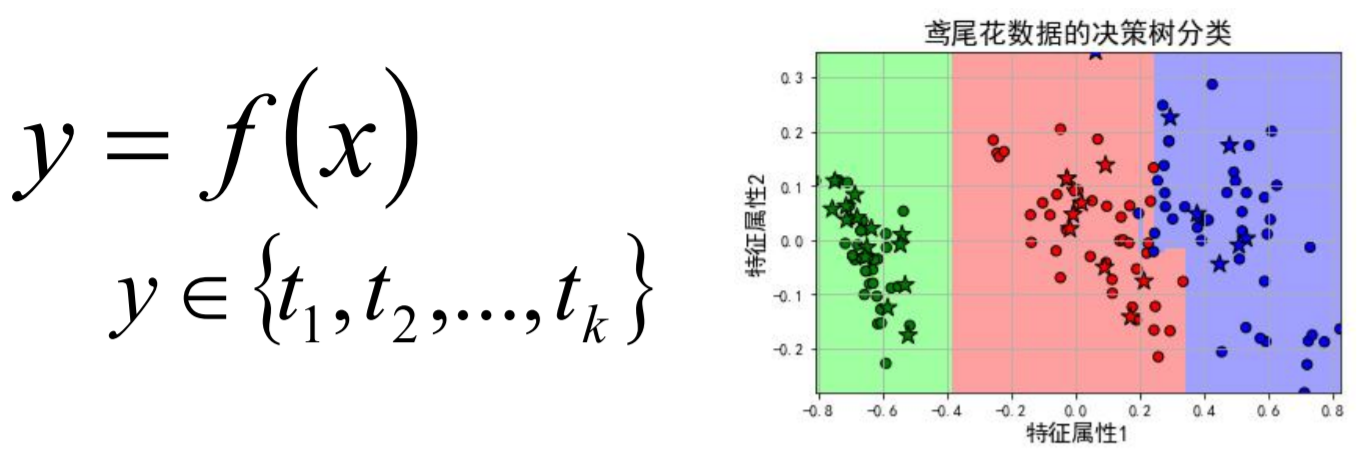
单标签多分类问题
单标签多分类问题其实是指待预测的label标签只有一个,但是label标签的取值可能有多种情况;直白来讲就是每个实例的可能类别有K种(t1 ,t2 ,...tk ,k≥3);常见 算法:Softmax、KNN、决策树等;
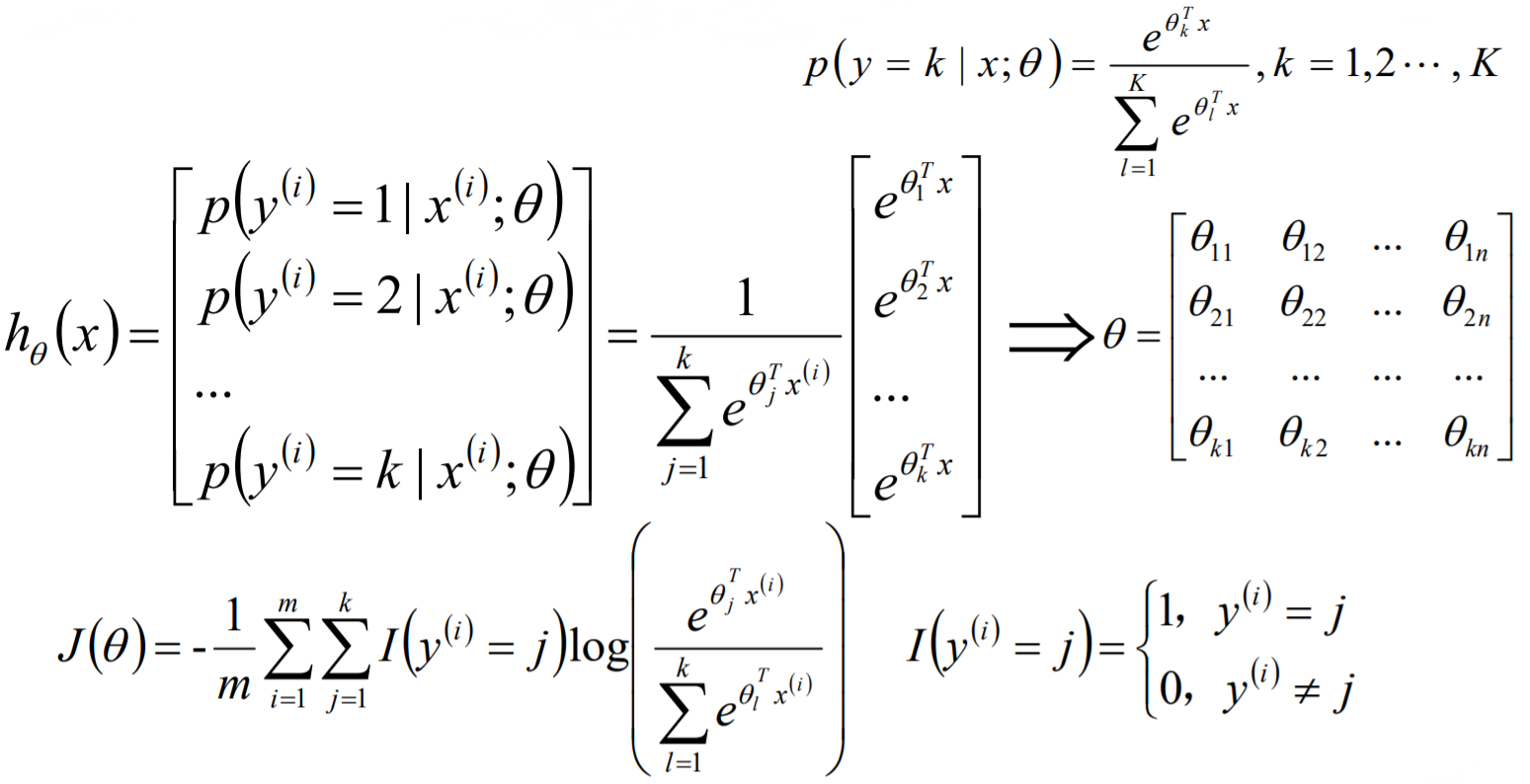
在实际的工作中,如果是一个多分类的问题,我们可以将这个待求解的问题转换 为二分类算法的延伸,即将多分类任务拆分为若干个二分类任务求解,具体的策 略如下:
- One-Versus-One(ovo):一对一
- One-Versus-All / One-Versus-the-Rest(ova/ovr): 一对多
- Error Correcting Output codes(纠错码机制):多对多
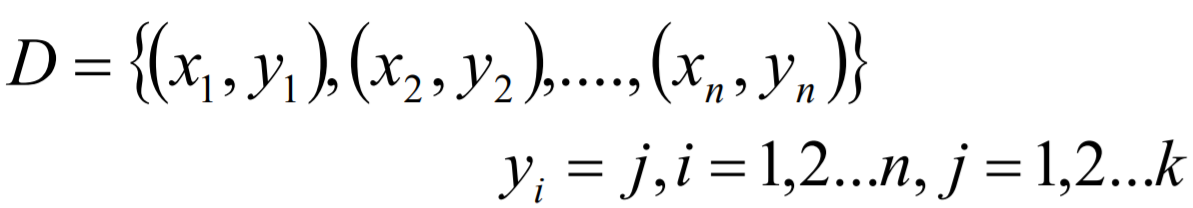
ovo
原理:将K个类别中的两两类别数据进行组合,然后使用组合后的数据训练出来一个模型,从而产生K(K-1)/2个分类器,将这些分类器的结果进行融合,并将分类器的预测结果使用多数投票的方式输出最终的预测结果值。
def ovo(datas,estimator): '''datas[:,-1]为目标属性''' import numpy as np Y = datas[:,-1] X = datas[:,:-1] y_value = np.unique(Y) #计算类别数目 k = len(y_value) modles = [] #将K个类别中的两两类别数据进行组合,并对y值进行处理 for i in range(k-1): c_i = y_value[i] for j in range(i+1,k): c_j = y_value[j] new_datas = [] for x,y in zip(X,Y): if y == c_i or y == c_j: new_datas.append(np.hstack((x,np.array([2*float(y==c_i)-1])))) new_datas = np.array(new_datas) algo = estimator() modle = algo.fit(new_datas) modles.append([(c_i,c_j),modle]) return modles def argmaxcount(seq): '''计算序列中出现次数最多元素''' '''超极简单的方法''' # from collections import Counter # return Counter(seq).values[0] '''稍微复杂的''' # dict_num = {} # for item in seq: # if item not in dict_num.keys(): # dict_num[item] = seq.count(item) # # 排序 # import operator # sorted(dict_num.items(), key=operator.itemgetter(1)) '''字典推导''' dict_num = dict_num = {i: seq.count(i) for i in set(seq)} def ovo_predict(X,modles): import operator result = [] for x in X: pre = [] for cls,modle in modles: pre.append(cls[0] if modle.predict(x) else cls[1]) d = {i: pre.count(i) for i in set(pre)} #利用集合的特性去重 result.append(sorted(d.items(),key=operator.itemgetter(1))[-1][0]) return result

from sklearn import datasets from sklearn.multiclass import OneVsOneClassifier from sklearn.svm import LinearSVC from sklearn.neighbors import KNeighborsClassifier # 加载数据 iris = datasets.load_iris() # 获取X和y X, y = iris.data, iris.target print("样本数量:%d, 特征数量:%d" % X.shape) # 设置为3,只是为了增加类别,看一下ovo和ovr的区别 y[-1] = 3 # 模型构建 clf = OneVsOneClassifier(LinearSVC(random_state=0)) # clf = OneVsOneClassifier(KNeighborsClassifier()) # 模型训练 clf.fit(X, y) # 输出预测结果值 print(clf.predict(X)) print("效果:{}".format(clf.score(X, y))) # 模型属性输出 k = 1 for item in clf.estimators_: print("第%d个模型:" % k, end="") print(item) k += 1 print(clf.classes_)
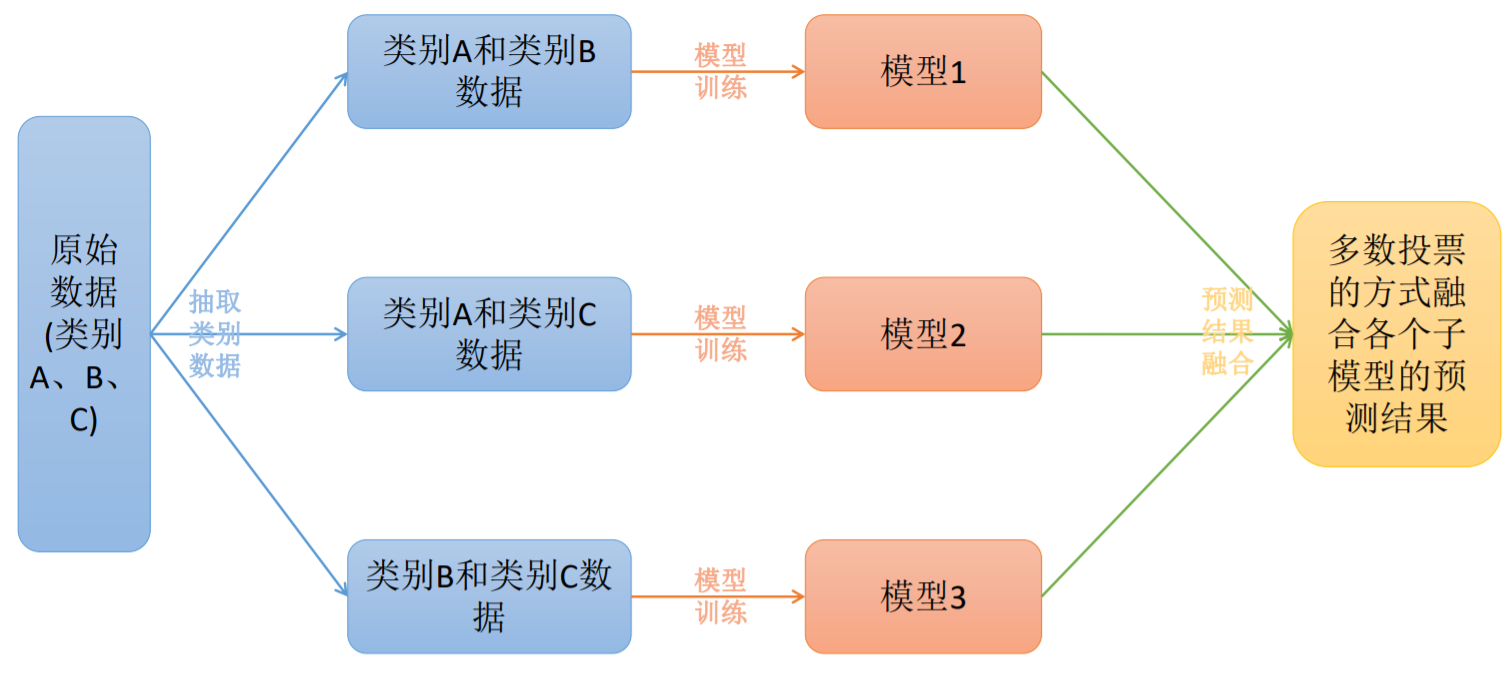
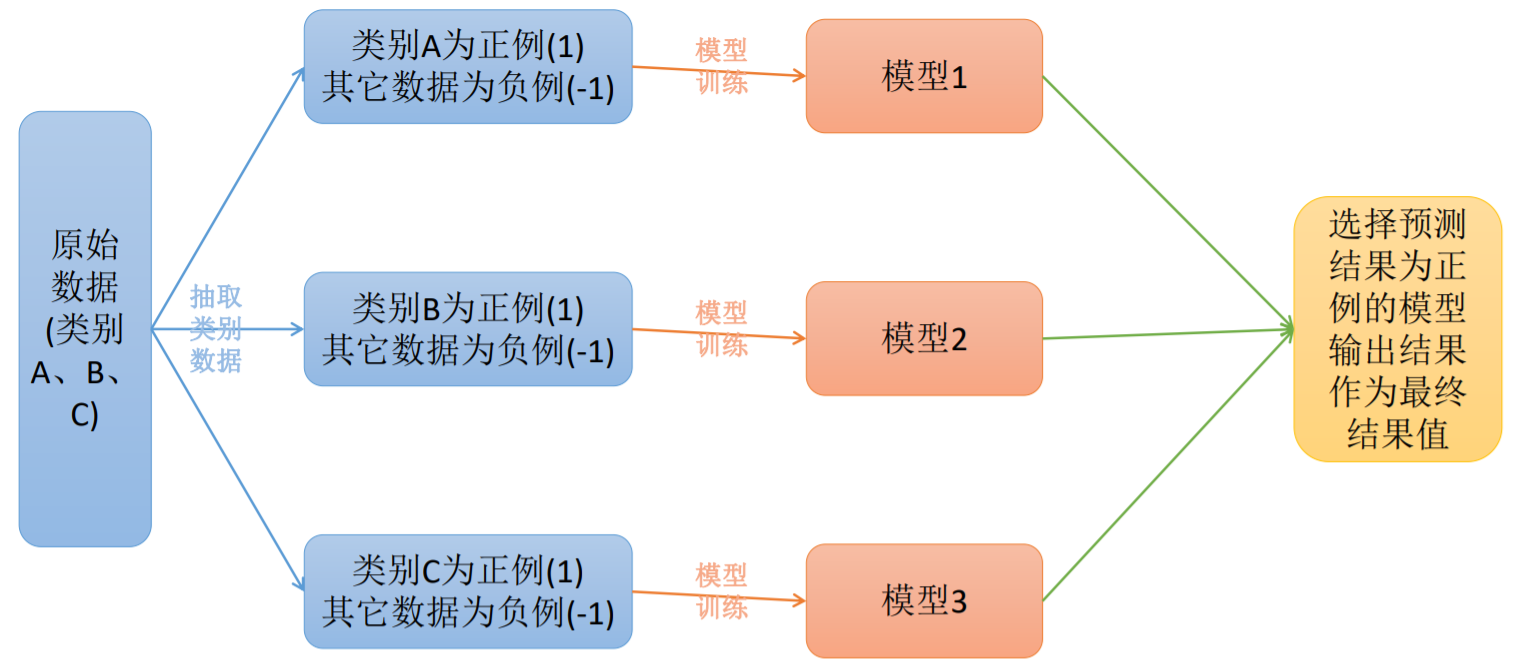
ovr
原理:在一对多模型训练中,不是两两类别的组合,而是将每一个类别作为正例,其它剩余的样例作为反例分别来训练K个模型;然后在预测的时候,如果在这K个模型中,只有一个模型输出为正例,那么最终的预测结果就是属于该分类器的这个类别;如果产生多个正例,那么则可以选择根据分类器的置信度作为指标,来选择置信度最大的分类器作为最终结果,常见置信度:精确度、召回率。
def ovr(datas,estimator): '''datas[:,-1]为目标属性''' import numpy as np Y = datas[:,-1] X = datas[:,:-1] y_value = np.unique(Y) #计算类别数目 k = len(y_value) modles = [] #准备K个模型的训练数据,并对y值进行处理 for i in range(k): c_i = y_value[i] new_datas = [] for x,y in zip(X,Y): new_datas.append(np.hstack((x,np.array([2*float(y==c_i)-1])))) new_datas = np.array(new_datas) algo = estimator() modle = algo.fit(new_datas) confidence = modle.score(new_datas) #计算置信度 modles.append([(c_i,confidence),modle]) return modles def ovr_predict(X,modles): import operator result = [] for x in X: pre = [] cls_confi = [] for cls,modle in modles: cls_confi.append(cls) pre.append(modle.predict(x)) pre_res = [] for c,p in zip(cls_confi,pre): if p == 1: pre_res.append(c) if not pre_res: pre_res = cls_confi result.append(sorted(pre_res,key=operator.itemgetter(1))[-1][0]) return result

from sklearn import datasets from sklearn.multiclass import OneVsRestClassifier from sklearn.svm import LinearSVC from sklearn.metrics import accuracy_score # 数据获取 iris = datasets.load_iris() X, y = iris.data, iris.target print("样本数量:%d, 特征数量:%d" % X.shape) # 设置为3,只是为了增加类别,看一下ovo和ovr的区别 y[-1] = 3 # 模型创建 clf = OneVsRestClassifier(LinearSVC(random_state=0)) # 模型构建 clf.fit(X, y) # 预测结果输出 print(clf.predict(X)) # 模型属性输出 k = 1 for item in clf.estimators_: print("第%d个模型:" % k, end="") print(item) k += 1 print(clf.classes_)
OvO和OvR的区别

Error Correcting
原理:将模型构建应用分为两个阶段:编码阶段和解码阶段;编码阶段中对K个类别中进行M次划分,每次划分将一部分数据分为正类,一部分数据分为反类,每次划分都构建出来一个模型,模型的结果是在空间中对于每个类别都定义了一个点;解码阶段中使用训练出来的模型对测试样例进行预测,将预测样本对应的点和类别之间的点求距离,选择距离最近的类别作为最终的预测类别。


from sklearn import datasets from sklearn.multiclass import OutputCodeClassifier from sklearn.svm import LinearSVC from sklearn.metrics import accuracy_score # 数据获取 iris = datasets.load_iris() X, y = iris.data, iris.target print("样本数量:%d, 特征数量:%d" % X.shape) # 模型对象创建 # code_size: 指定最终使用多少个子模型,实际的子模型的数量=int(code_size*label_number) # code_size设置为1,等价于ovr子模型个数; # 设置为0~1, 那相当于使用比较少的数据划分,效果比ovr差; # 设置为大于1的值,那么相当于存在部分模型冗余的情况 clf = OutputCodeClassifier(LinearSVC(random_state=0), code_size=30, random_state=0) # 模型构建 clf.fit(X, y) # 输出预测结果值 print(clf.predict(X)) print("准确率:%.3f" % accuracy_score(y, clf.predict(X))) # 模型属性输出 k = 1 for item in clf.estimators_: print("第%d个模型:" % k, end="") print(item) k += 1 print(clf.classes_)
多标签算法问题
Multi-Label Machine Learning(MLL算法)是指预测模型中存在多个y值,具体分为两类不同情况:
- 多个待预测的y值;
- 在分类模型中, 一个样例可能存在多个不固定的类别。
根据多标签业务问题的复杂性,可以将问题分为两大类:
- 待预测值之间存在相互的依赖关系;
- 待 预测值之间是不存在依赖关系的。
对于这类问题的解决方案可以分为两大类:
- 转换策略(Problem Transformation Methods);
- 算法适应(Algorithm Adaptation)。
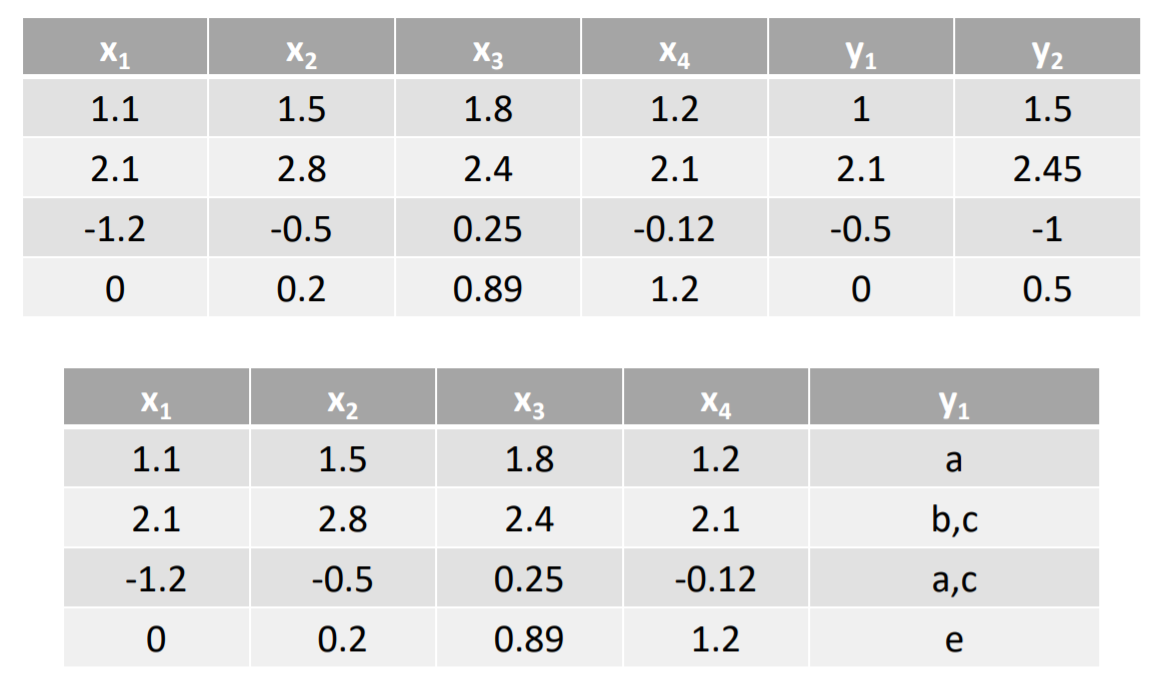
注意:在多标签中一般认为每个标签只有两个类别,即(+1,和 - 1),如果一个标签有多个类别,则需要把类别分解成取值为+1或者- 1的新标签。
Problem Transformation Methods
Problem Transformation Methods又叫做策略转换或者问题转换,是一种将多标签的分类问题转换成为单标签模型构造的问题,然后将模型合并的一种方式,主要有以下几种方式:
- Binary Relevance(first-order)
- Classifier Chains(high-order)
- Calibrated Label Ranking(second-order)
Binary Relevance
Binary Relevance的核心思想是将多标签分类问题进行分解,将其转换为q个二元分类问题,其中每个二元分类器对应一个待预测的标签。
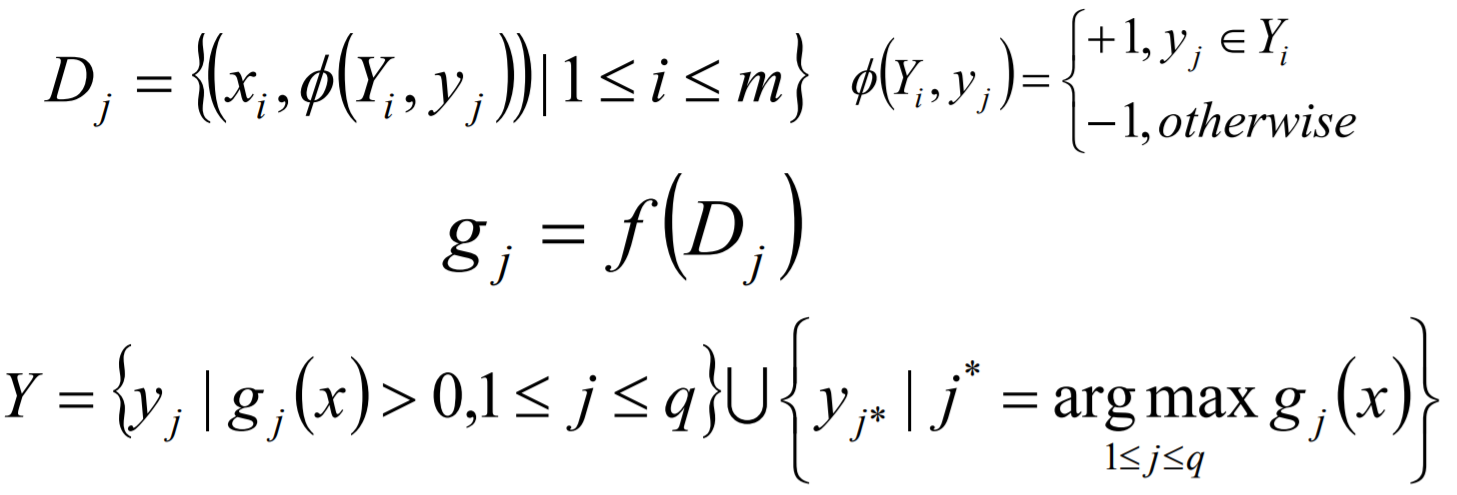
def Binary_Relevance(X,Y,estimator): '''Y是一个只有0和1的数组''' import numpy as np # 计算标签的个数 q = Y.shape[1] Y_label = [i for i in range(q)] modles = [] #准备K个模型的训练数据,并对y值进行处理 for j in Y_label: D_j = [] for x,y in zip(X,Y): D_j.append(np.hstack((x,np.array([1 if j in Y_label[y==1] else -1])))) new_datas = np.array(D_j) algo = estimator() g_j = algo.fit(new_datas) modles.append(g_j) # Y = Y.replace(0,-1) #把所有的0替换成-1 # for j in Y_label: # new_datas = np.hstack((X,Y[:,j].reshape(-1,1))) # new_datas = np.array(new_datas) # algo = estimator() # g_j = algo.fit(new_datas) # modles.append(g_j) return modles def Binary_Relevance_predict(X,modles,label_name): import operator result = [] for x in X: pre_res = [] for g_j in modles: pre_res.append(g_j.predict(x)) Y = set(np.array(label_name)[np.array(pre_res)>0]).union(label_name[pre_res.index(max(pre_res))]) result.append(Y) return result
Binary Relevance方式的优点如下:
- 实现方式简单,容易理解;
- 当y值之间不存在相关的依赖关系的时候,模型的效果不错。
缺点如下:
- 如果y直接存在相互的依赖关系,那么最终构建的模型的泛化能力比较弱;
- 需要构建q个二分类器,q为待预测的y值数量,当q比较大的时候,需要构建的模型 会比较多。
Classifier Chains
Classifier Chains的核心思想是将多标签分类问题进行分解,将其转换成为一个二元分类器链的形式,其中链后的二元分类器的构建是在前面分类器预测结果的基础上的。在模型构建的时候,首先将标签顺序进行shuffle打乱排序操作,然后按照从头到尾分别构建每个标签对应的模型。

Classifier Chains模型构建

Classifier Chains模型预测
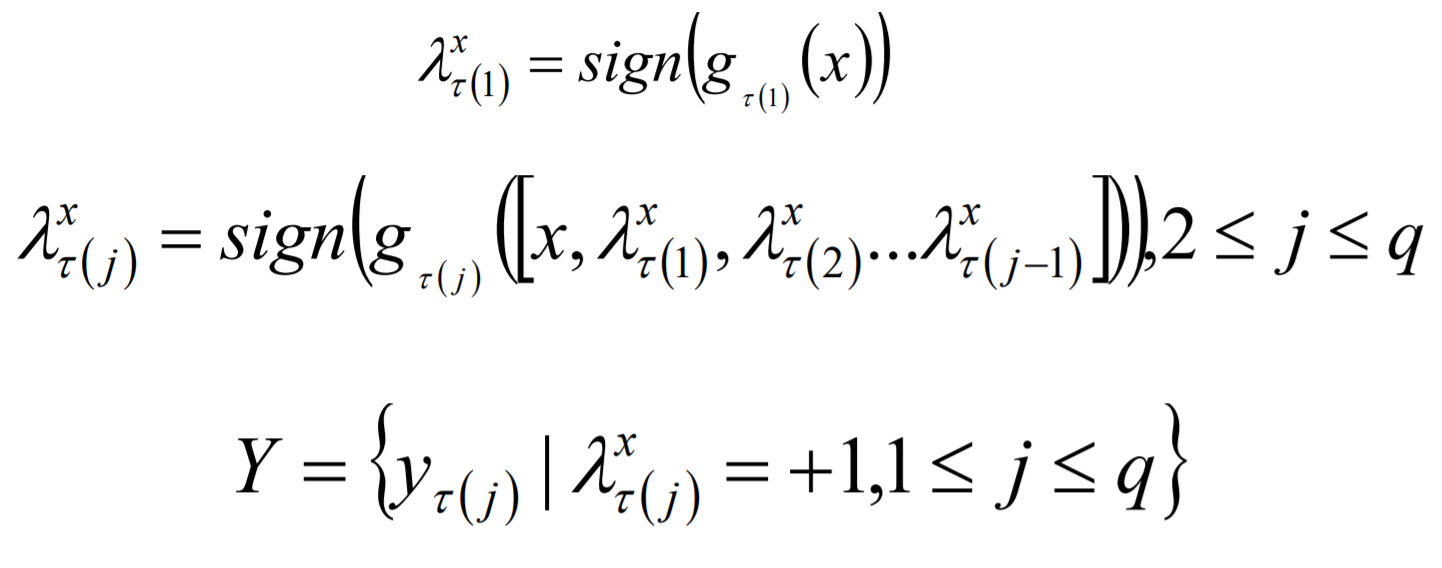
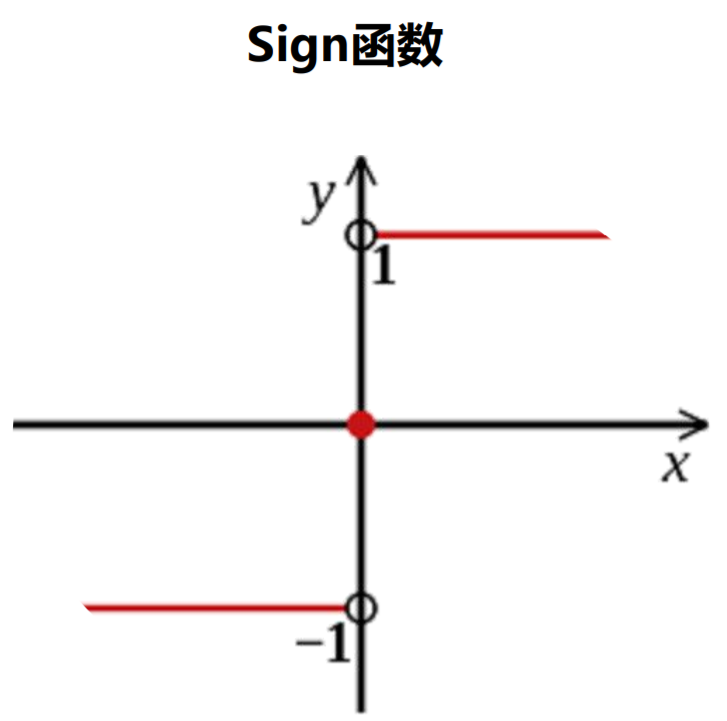
Classifier Chains方式的优点如下:
- 实现方式相对比较简单,容易理解;
- 考虑标签之间的依赖关系,最终模型的泛化能力相对于Binary Relevance方式构建的模型效果要好。
缺点如下: 很难找到一个比较适合的标签依赖关系。
Calibrated Label Ranking
Calibrated Label Ranking的核心思想是将多标签分类问题进行分解,将其转换为标签的排序问题,最终的标签就是排序后最大的几个标签值。
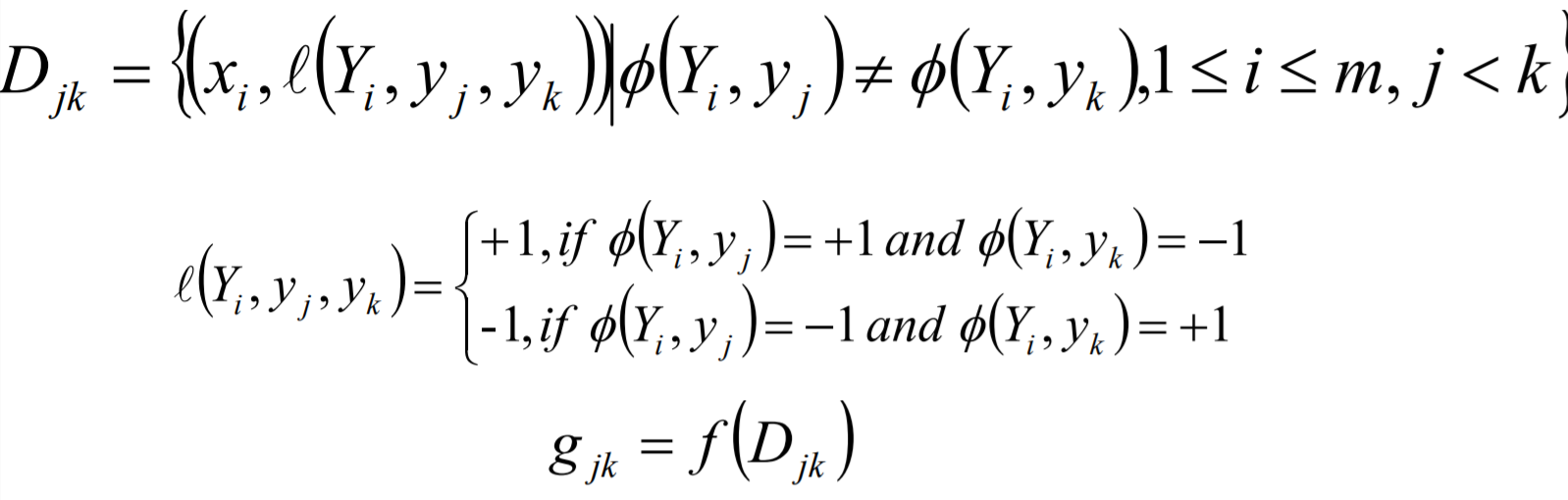

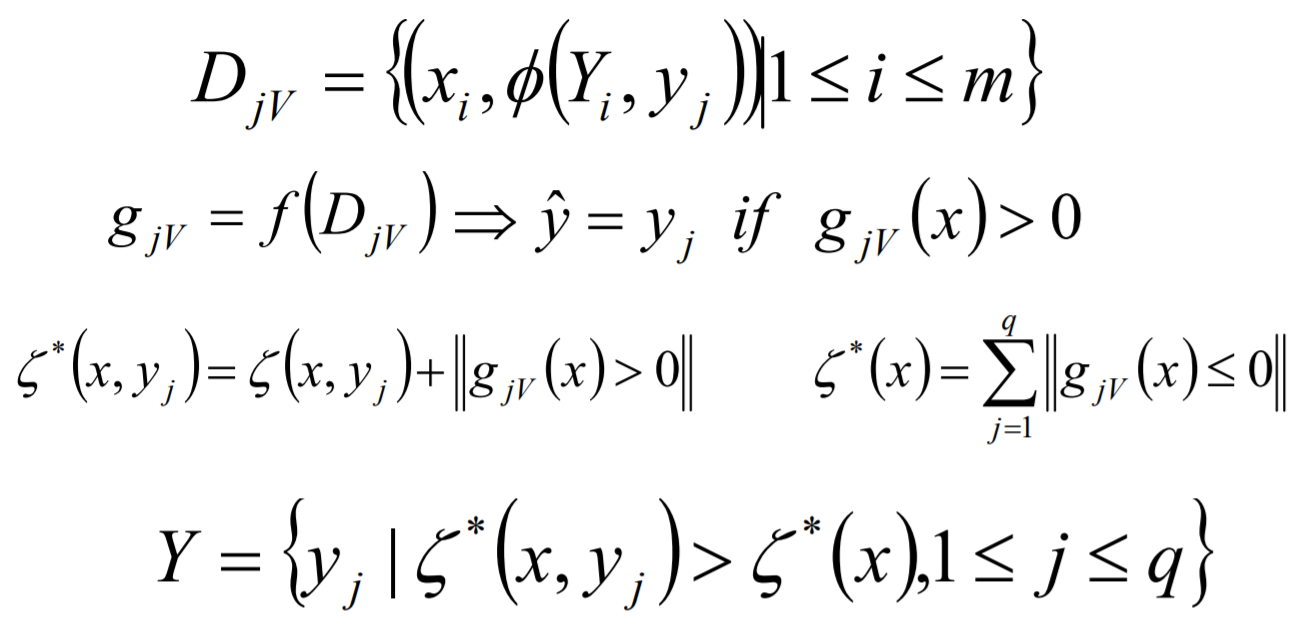
Calibrated Label Ranking 方式的优点如下:
- 考虑了标签两两组合的情况,最终的模型相对来讲泛化能力比较好。
缺点如下:
- 只考虑两两标签的组合,没有考虑到标签与标签之间的所有依赖关系。

import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import make_multilabel_classification from sklearn.multioutput import MultiOutputClassifier from sklearn.svm import SVC from sklearn.preprocessing import LabelBinarizer from sklearn.decomposition import PCA def plot_hyperplane(clf, min_x, max_x, linestyle, label): # 画图 w = clf.coef_[0] a = -w[0] / w[1] xx = np.linspace(min_x - 5, max_x + 5) yy = a * xx - (clf.intercept_[0]) / w[1] plt.plot(xx, yy, linestyle, label=label) def plot_subfigure(X, Y, subplot, title): # 将X进行降维操作,变成两维的数据 X = PCA(n_components=2).fit_transform(X) min_x = np.min(X[:, 0]) max_x = np.max(X[:, 0]) min_y = np.min(X[:, 1]) max_y = np.max(X[:, 1]) classif = MultiOutputClassifier(SVC(kernel='linear')) classif.fit(X, Y) plt.subplot(2, 2, subplot) plt.title(title) zero_class = np.where(Y[:, 0]) one_class = np.where(Y[:, 1]) plt.scatter(X[:, 0], X[:, 1], s=40, c='gray') plt.scatter(X[zero_class, 0], X[zero_class, 1], s=160, edgecolors='b', facecolors='none', linewidths=2, label='Class 1') plt.scatter(X[one_class, 0], X[one_class, 1], s=80, edgecolors='orange', facecolors='none', linewidths=2, label='Class 2') plot_hyperplane(classif.estimators_[0], min_x, max_x, 'r--', 'Boundary\nfor class 1') plot_hyperplane(classif.estimators_[1], min_x, max_x, 'k-.', 'Boundary\nfor class 2') plt.xticks(()) plt.yticks(()) plt.xlim(min_x - .5 * max_x, max_x + .5 * max_x) plt.ylim(min_y - .5 * max_y, max_y + .5 * max_y) if subplot == 1: plt.xlabel('First principal component') plt.ylabel('Second principal component') plt.legend(loc="upper left") plt.figure(figsize=(8, 6)) X, Y = make_multilabel_classification(n_classes=2, allow_unlabeled=False, # 该参数控制是否有类别缺省的数据,False表示没有 random_state=1) plot_subfigure(X, Y, 1, "With unlabeled samples + CCA") plt.subplots_adjust(.04, .02, .97, .94, .09, .2) plt.show()

import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import make_multilabel_classification from sklearn.multiclass import OneVsRestClassifier from sklearn.svm import SVC from sklearn.preprocessing import LabelBinarizer from sklearn.decomposition import PCA def plot_hyperplane(clf, min_x, max_x, linestyle, label): # 画图 w = clf.coef_[0] a = -w[0] / w[1] xx = np.linspace(min_x - 5, max_x + 5) yy = a * xx - (clf.intercept_[0]) / w[1] plt.plot(xx, yy, linestyle, label=label) def plot_subfigure(X, Y, subplot, title): # 将X进行降维操作,变成两维的数据 X = PCA(n_components=2).fit_transform(X) min_x = np.min(X[:, 0]) max_x = np.max(X[:, 0]) min_y = np.min(X[:, 1]) max_y = np.max(X[:, 1]) classif = OneVsRestClassifier(SVC(kernel='linear')) classif.fit(X, Y) plt.subplot(2, 2, subplot) plt.title(title) zero_class = np.where(Y[:, 0]) one_class = np.where(Y[:, 1]) plt.scatter(X[:, 0], X[:, 1], s=40, c='gray') plt.scatter(X[zero_class, 0], X[zero_class, 1], s=160, edgecolors='b', facecolors='none', linewidths=2, label='Class 1') plt.scatter(X[one_class, 0], X[one_class, 1], s=80, edgecolors='orange', facecolors='none', linewidths=2, label='Class 2') plot_hyperplane(classif.estimators_[0], min_x, max_x, 'r--', 'Boundary\nfor class 1') plot_hyperplane(classif.estimators_[1], min_x, max_x, 'k-.', 'Boundary\nfor class 2') plt.xticks(()) plt.yticks(()) plt.xlim(min_x - .5 * max_x, max_x + .5 * max_x) plt.ylim(min_y - .5 * max_y, max_y + .5 * max_y) if subplot == 1: plt.xlabel('First principal component') plt.ylabel('Second principal component') plt.legend(loc="upper left") plt.figure(figsize=(8, 6)) X, Y = make_multilabel_classification(n_classes=2, n_labels=1, allow_unlabeled=False, # 该参数控制是否有类别缺省的数据,False表示没有 random_state=1) plot_subfigure(X, Y, 1, "With unlabeled samples + CCA") plt.subplots_adjust(.04, .02, .97, .94, .09, .2) plt.show()
Algorithm Adaptation
Algorithm Adaptation又叫做算法适应性策略,是一种将现有的单标签的算法直接应用到多标签上的一种方式,主要有以下几种方式:
k近邻算法(k-Nearest Neighbour, KNN)的思想:如果一个样本在特征空间中的k个最相似(即特征空间中距离最近)的样本中的大多数属于某一个类别,那么该样本属于这个类别。
ML-kNN的思想:对于每一个实例来讲,先获取距离它最近的k个实例,然后使用这些实例的标签集合,通过最大后验概率(MAP)来判断这个实例的预测标签集合的值。
最大后验概率(MAP):其实就是在最大似然估计(MLE)中加入了这个要估计量 的先验概率分布。
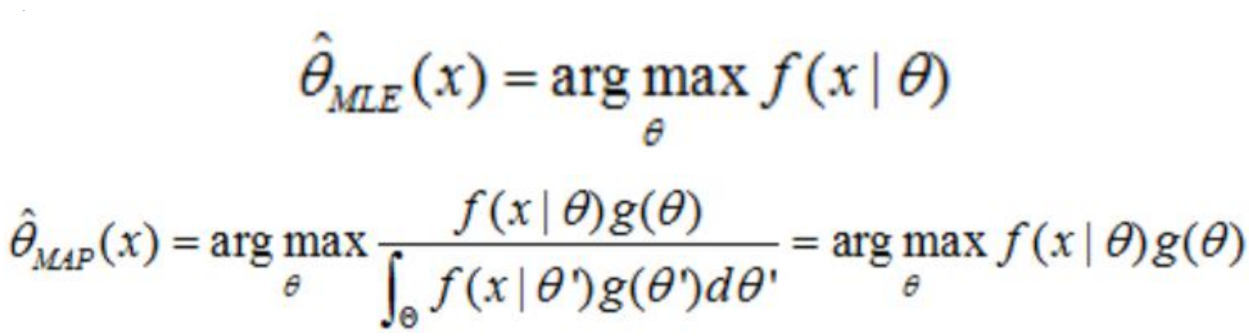
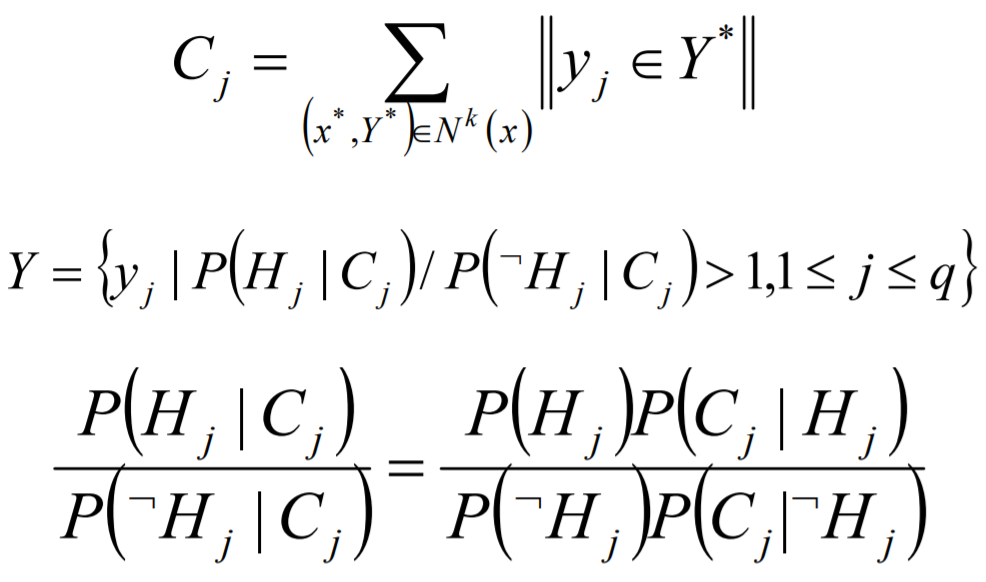
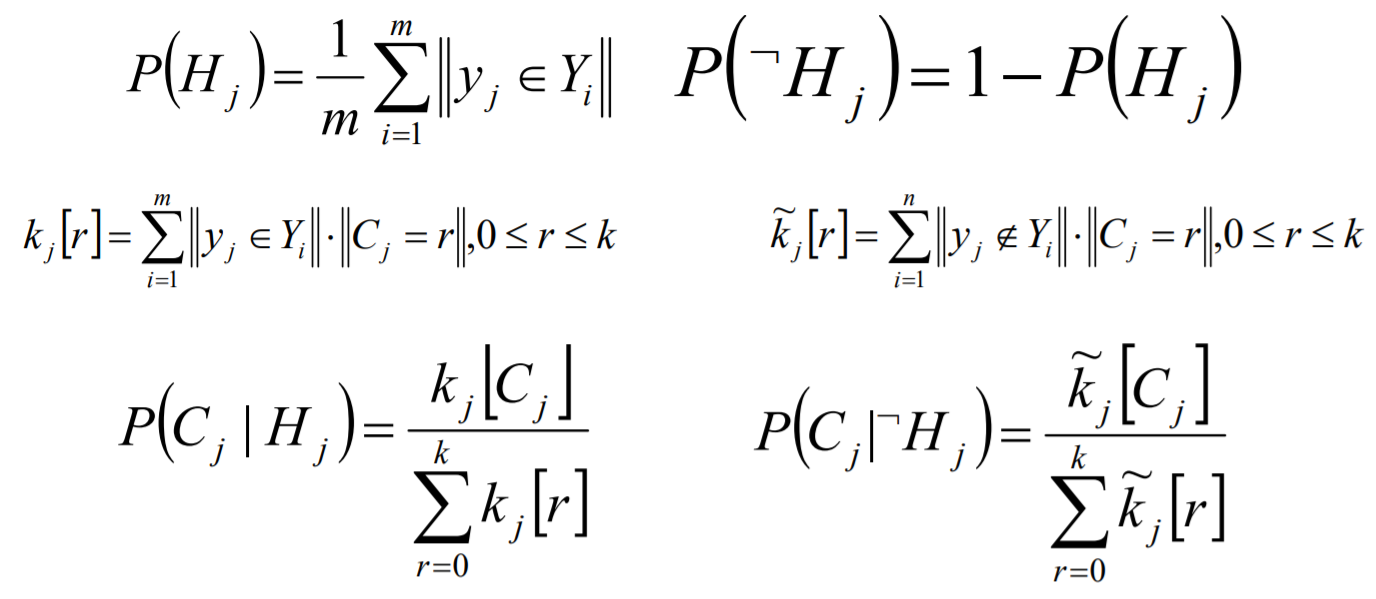
ML-DT是使用决策树处理多标签内容,核心在于给予更细粒度的信息殇增益准则来构建这个决策树模型。