SIFT特征匹配原理及源代码
特征匹配部分由ORB篇已介绍OPENCV中特征匹配需要用到的一些函数和类的封装完成，本篇不再介绍。SIFT和SURF由于版权问题，（SIFT在2020年（今年）3月6日专利有限期20年过期，OPENCV后续的版本中可能会有相应接口。）在opencv4.1+中没有函数接口，可通过安装对应版本的opencv-contrib进行使用。
1 背景
SIFT（Scale Invariant Feature Transform，尺度不变特征变换匹配算法）由David G. Lowe教授在1999年（《Object Recognition from Local Scale-Invariant Features》）提出，在2004年（《Distinctive Image Features from Scale-Invariant Keypoints》）得以完善。SIFT可以应用到物体辨识、机器人地图感知与导航、影像缝合、3D模型建立、手势辨识、影像追踪和动作比对等方向。SIFT 特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。对于光线、噪声、些微视角改变的容忍度也相当高。基于这些特性，它们是高度显著而且相对容易撷取，在母数庞大的特征数据库中，很容易辨识物体而且鲜有误认。使用 SIFT特征描述对于部分物体遮蔽的侦测率也相当高，甚至只需要3个以上的SIFT物体特征就足以计算出位置与方位。在现今的电脑硬件速度下和小型的特征数据库条件下，辨识速度可接近即时运算。SIFT特征的信息量大，适合在海量数据库中快速准确匹配，最大的缺点是计算量大、运行时间相对较长。
2 SIFT特征原理
2.1概述
SIFT算法通过金字塔出现的构造进行不同尺度的特征点的提取和描述子的计算。整体可分为四个步骤：尺度空间极值检测、关键点定位、方向计算和关键点描述子计算。下面按步骤介绍。
2.2尺度空间极值检测：
尺度空间方法将传统的单尺度图像信息处理技术纳入尺度不断变化的动态分析框架中，更容易获取图像的本质特征。可用于表示轮廓在不同尺度下的形状、大小和位置等。通过构建尺度空间，满足检测出的像素点的尺度不变特性。
尺度空间的构建可采用高斯模糊卷积核进行构建，SIFT算法中通过高斯核与图像的卷积操作，达到图像不同尺度下的表示效果。详细如下。
高斯卷积核中每个值的大小如下：
其中σ表示方差，通过改变σ值的大小，获取不同尺度对应的高斯卷积核。高斯卷积核与图像的公式如下：
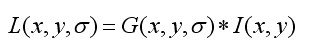
L表示输出图像，G表示二维高斯卷积核，I表示输入图像的像素值。*表示进行卷积运算。σ 可表示为尺度空间因子。
在SIFT算法中，采用图像金字塔的方式表示尺度空间因子。整个金字塔可分为两部分：从上到下分为多组和每组包含多层。
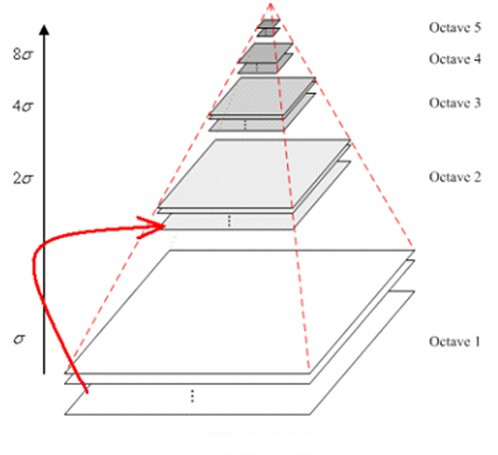
如上图，最下面一组的第一层为原图像。第二组的第一层图像通过对第一组的倒数第三层图像下采样获取。依次类推直到得到所需的组数。对每一组，通过采用不同σ大小的高斯卷积核进行卷积得到多层图像。其中σ的公式如下：
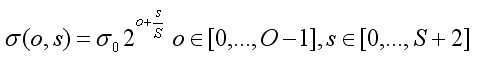
其中o表示为组数，s表示为层数,S表示为层总数。
2002年，研究者发现尺度归一化的高斯拉普拉斯函数相对于其它的特征提取函数，可产生更稳定的特征。其中高斯拉普拉斯函数:
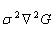
而早在1994年，有研究者发现高斯差分函数（简称DOG算子）与尺度归一化的高斯拉普拉斯函数非常近似。其中高斯拉普拉斯函数与D（x,y, σ）的关系可通过如下推导：
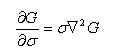
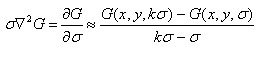
SIFT算法作者使用高效的高斯差分替换拉普拉斯算子进行角点检测。公式如下：
D（x,y,σ) = (G(x,y,kσ)-G(x,y,σ))*I(x,y) = L(x,y,kσ)-L(x,y,σ)
在构建好尺度空间后，为寻找空间中的极值点，SIFT算法通过将像素点与周围所有相邻点的像素值的大小进行比较，判断其是否为极值点。如下图
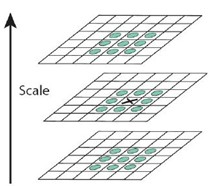
将中间点与周围8个点和上下两层共9*2共26点进行比较，确保在尺度空间和二维空间均检测到极值点。（判断是否在相邻中，像素值最大或最小）。
2.3 关键点定位：
通过 2.2可得到离散空间的极值点，SIFT算法通过拟合二次函数，精确关键点的位置，同时去除低对比度的关键点和不稳定的边缘相应点以增强匹配稳定性和提高抗噪能力。
通过上述计算，得到的像素点坐标均以整数为单位，在像素点之间仍有无数的点未考虑。下图为离散空间极值点与连续空间极值点之间的区别。
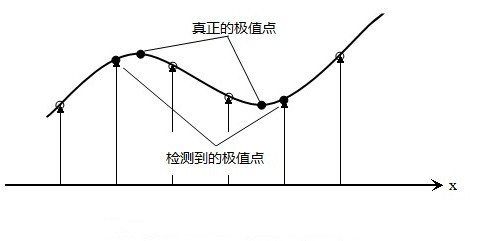
为求取连续空间上的极值点，可通过对尺度空间DOG函数进行泰勒展开求解：
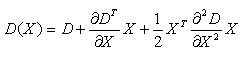
其中，X=（x,y,σ)T。对上式求导，并让方程等于零，得到极值点的偏移量和方程的值分别为：
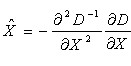
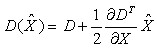
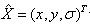代表相对插值中心的偏移量，当它的任一维度上的偏移量大于0.5时，以为插值中心偏移到相邻的像素点上，应改变当前的关键点的位置，在新的位置上反复插值直到收敛。同时。|D(x)|小于某个值的点时，易受噪声的干扰而变得不稳定，SIFT算法将|D(x)|小于某个经验值的极值点删除。
通过DOG算子计算得到极值点，可产生较强的边缘响应，需要剔除不稳定的边缘响应点。SIFT算法通过采用Harris检测算法进一步削弱边缘不稳定性，详细如下。
首先得到一个Hessian矩阵：
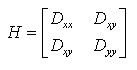
H的特征值α和β可表示为x和y方向的梯度，得下列公式：
Trace(H) = Dxx+Dyy = α+β,
Det(H) = DxxDyy -(Dxy)2 =αβ
对α和β,假设α=rβ，得到：
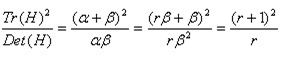
当r=1时，上式有最小值。由Harris篇可知，当α和β的比例越大时（即像素值一个方向变化很大，另一方向变化小），极可能为边缘上的点。故为剔除边缘响应点，需让该比值小于一定的阈值，可通过检测在某阈值r下，是否符合下列等式即可(SIFT发表文章中,r取值为10)：
2.4 关键点方向计算：
通过上述算法得到的关键点仍不具备旋转不变形，SIFT通过采集其所在高斯金字塔图像的3σ领域窗口像素的幅度值和方向分布特征获取角度信息，计算如下：
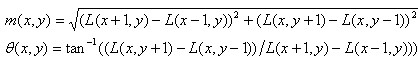
其中，m(x,y)表示梯度值，θ表示该像素点的角度。通过上述公式计算像素点周围邻域窗口每个点的像素的幅度值和方向大小，再通过统计直方图的方式进行方向的确定，详细如下。
首先将0~360度划分为36个部分，每个部分的范围为10°，进行直方图统计，图像表示如下：
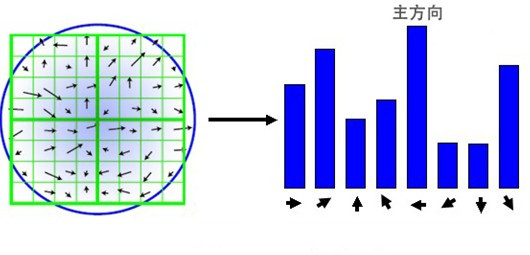
其中，峰值代表关键点的主方向。同时为增强特征匹配的鲁棒性，保留峰值大于主方向峰值80%的方向作为关键点的辅方向。
2.5 描述子计算：
通过上述步骤，计算出的关键点拥有三个信息：位置、尺度和方向。在进行特征匹配时，仍需要一个描述符用于特征匹配。SIFT算法描述符的计算可分为4部分，下面按步骤进行介绍。
2.5.1 确定计算描述子所需的图像区域：
特征描述子的计算与点所在尺度有关，因此对关键点的梯度的计算应在对应的高斯图像上进行。SIFT算法将关键点附近的邻域划分为d*d（一般为4）个子区域，每个子区域做为一个种子点，每个种子点有8个方向。每个子区域的大小与2.4计算关键点的方向相同，均为3σ。
2.5.2 旋转图像：
对于2.5.1的图像区域，根据2.4计算得到的主方向，进行旋转，旋转公式如下：
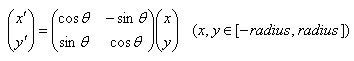
2.5.3 子区域种子点的角度分配：
对图像进行旋转后，计算每个子区域内的梯度值和方向，通过加权函数分配到对应种子点的8个方向上。
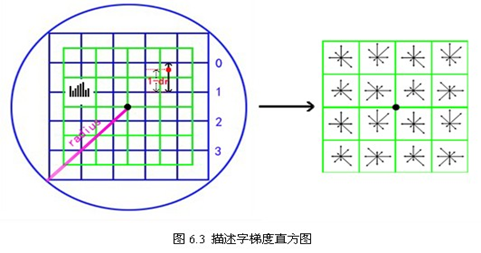
如上图所示，其中右右图可表示为每个种子点的方向信息。
2.5.4 描述子计算：
通过2.5.3，得到的4*4*8=128个梯度信息即为该关键点的特征向量。在形成特征向量后，为去除光照变化的影响，需进行归一化处理。归一化的数据即为该关键点的描述子。
3 代码实现
3.1 API和demo：
API:
/* 在opencv中，暂时没有SIFT的接口，需要通过安装opencv的扩展库opencv-contrib使用
*/
cv::Ptr<cv::xfeatures2d::SIFT> sift = cv::xfeatures2d::SIFT::create(int nfeatures = 0, int nOctaveLayers = 3, double contrastThreshold = 0.04, double edgeThreshold = 10, double sigma = 1.6);
//特征的数量，0表示计算每个特征方向，１表示不计算方向（速度更快）;表示金子塔的组数；用于过滤区域中的弱特征，阈值越大，特征越少；用于过滤类似边缘的阈值；高斯输入层级。
Demo:
#include"opencv2/opencv.hpp" #include"opencv2/xfeatures2d.hpp" using namespace std; using namespace cv; int main() { Mat src1 = imread("T-.png"); Mat src2 = imread("DT.png"); //特征点提取方法 cv::Ptr<cv::xfeatures2d::SIFT> sift = cv::xfeatures2d::SIFT::create(); //特征点提取 vector<KeyPoint> kp1,kp2; sift->detect(src1,kp1); sift->detect(src2,kp2); //画出特征点 Mat keypointImage1,key_pointImage2,descriptor1,descriptor2; drawKeypoints(src1,kp1,keypointImage1,cv::Scalar::all(-1),DrawMatchesFlags::DEFAULT); imshow("SIFTKP1",keypointImage1); drawKeypoints(src2,kp2,key_pointImage2,cv::Scalar(-1),DrawMatchesFlags::DEFAULT); imshow("SIFTKP2",key_pointImage2); cv::Mat match_pointL,match_pointR; sift->detectAndCompute(src1,cv::Mat(),kp1,match_pointL); sift->detectAndCompute(src2,cv::Mat(),kp2,match_pointR); if(match_pointL.type()!=CV_32F||match_pointR.type()!=CV_32F) { match_pointL.convertTo(match_pointL,CV_32F); match_pointL.convertTo(match_pointR,CV_32F); } vector<DMatch> matches; cv::Ptr<cv::DescriptorMatcher> matcher = cv::DescriptorMatcher::create("FlannBased"); matcher->match(match_pointL,match_pointR,matches); double maxDist = 10; for(int i =0;i<match_pointL.rows;i++) { double dist = matches[i].distance; if(dist>maxDist) maxDist= dist; } vector<DMatch> good_matches,need_matches; vector<float>distance; for(int i =0;i<match_pointL.rows;i++) { if(matches[i].distance<0.1*maxDist) ////调参褚 0.1越小 越精确 官方推荐0.5 如果确定点 可改变 { good_matches.push_back(matches[i]); distance.push_back(matches[i].distance); } } Mat imageOutput; cv::drawMatches(src1,kp1,src2,kp2,good_matches,imageOutput); vector<Point>first_image,second_image; for(int i =0;i<need_matches.size();i++) { first_image.push_back(kp1[need_matches[i].queryIdx].pt); second_image.push_back(kp2[need_matches[i].trainIdx].pt); } cv::imshow("匹配图片",imageOutput); waitKey(0); return 0; }
源代码：
/* 假设nOctaveLayers = 3 第0族第0幅： sigma=1.6 第0族第1幅： sigma=1.6 2^(1./3)*sigma 第0族第2幅： sigma=1.6 2^(2./3)*sigma 第0族第3幅： sigma=1.6 2^(3./3)*sigma 第0族第4幅： sigma=1.6 2^(4./3)*sigma 第0族第5幅： sigma=1.6 2^(5./3)*sigma 第0族-->第1族 大小变为一半 尺度为2*sigma 用的是第三幅图像的sigma 第1族第0幅： sigma=1.6 2^(3./3)*sigma 第1族第1幅： sigma=1.6 2^(4./3)*sigma 第1族第2幅： sigma=1.6 2^(5./3)*sigma 第1族第3幅： sigma=1.6 2^(6./3)*sigma 第1族第4幅： sigma=1.6 2^(7./3)*sigma 第1族第5幅： sigma=1.6 2^(8./3)*sigma ..... 第o族第i幅： sigma=1.6 2^(o + i/3))*sigma gaussian pyramid 一共有nOctaves * （nOctaveLayers + 3）幅图像 */ void SIFT::buildGaussianPyramid( const Mat& base, vector<Mat>& pyr, int nOctaves ) const { vector<double> sig(nOctaveLayers + 3); pyr.resize(nOctaves*(nOctaveLayers + 3)); // precompute Gaussian sigmas using the following formula: // \sigma_{total}^2 = \sigma_{i}^2 + \sigma_{i-1}^2 // 之所以做 \sigma_{i}^2 = \sigma_{total}^2 - \sigma_{i-1}^2 // 是因为每一张图像都是在上一张图像的基础上做的高斯模糊，累计起来其实就是对原始图像做了2^(o-1)*2^(n-1/nOctaveLayers)尺度的高斯模糊 sig[0] = sigma; double k = pow( 2., 1. / nOctaveLayers ); for( int i = 1; i < nOctaveLayers + 3; i++ ) { double sig_prev = pow(k, (double)(i-1))*sigma; double sig_total = sig_prev*k; sig[i] = std::sqrt(sig_total*sig_total - sig_prev*sig_prev); } for( int o = 0; o < nOctaves; o++ ) { for( int i = 0; i < nOctaveLayers + 3; i++ ) { Mat& dst = pyr[o*(nOctaveLayers + 3) + i]; if( o == 0 && i == 0 ) dst = base; // base of new octave is halved image from end of previous octave else if( i == 0 ) { const Mat& src = pyr[(o-1)*(nOctaveLayers + 3) + nOctaveLayers]; resize(src, dst, Size(src.cols/2, src.rows/2), 0, 0, INTER_NEAREST); } else { const Mat& src = pyr[o*(nOctaveLayers + 3) + i-1]; GaussianBlur(src, dst, Size(), sig[i], sig[i]); } } } } /* DOG Pyramid 一共有nOctaves * （nOctaveLayers + 2）幅图像 */ void SIFT::buildDoGPyramid( const vector<Mat>& gpyr, vector<Mat>& dogpyr ) const { int nOctaves = (int)gpyr.size()/(nOctaveLayers + 3); dogpyr.resize( nOctaves*(nOctaveLayers + 2) ); for( int o = 0; o < nOctaves; o++ ) { for( int i = 0; i < nOctaveLayers + 2; i++ ) { const Mat& src1 = gpyr[o*(nOctaveLayers + 3) + i]; const Mat& src2 = gpyr[o*(nOctaveLayers + 3) + i + 1]; Mat& dst = dogpyr[o*(nOctaveLayers + 2) + i]; subtract(src2, src1, dst, noArray(), DataType<sift_wt>::type); } } } // // Interpolates a scale-space extremum's location and scale to subpixel // accuracy to form an image feature. Rejects features with low contrast. // Based on Section 4 of Lowe's paper. static bool adjustLocalExtrema( const vector<Mat>& dog_pyr, KeyPoint& kpt, int octv, int& layer, int& r, int& c, int nOctaveLayers, float contrastThreshold, float edgeThreshold, float sigma ) { const float img_scale = 1.f/(255*SIFT_FIXPT_SCALE); //图像的尺度，将uchar型的图像数转化为0~1之间的图像 const float deriv_scale = img_scale*0.5f; const float second_deriv_scale = img_scale; const float cross_deriv_scale = img_scale*0.25f; float xi=0, xr=0, xc=0, contr=0; int i = 0; for( ; i < SIFT_MAX_INTERP_STEPS; i++ ) //SIFT_MAX_INTERP_STEPS为迭代次数 { int idx = octv*(nOctaveLayers+2) + layer; //取该特征点所在差分金字塔的位置索引 const Mat& img = dog_pyr[idx]; const Mat& prev = dog_pyr[idx-1]; const Mat& next = dog_pyr[idx+1]; Vec3f dD((img.at<sift_wt>(r, c+1) - img.at<sift_wt>(r, c-1))*deriv_scale, (img.at<sift_wt>(r+1, c) - img.at<sift_wt>(r-1, c))*deriv_scale, (next.at<sift_wt>(r, c) - prev.at<sift_wt>(r, c))*deriv_scale); //分别是对x,y,z轴的差分组成的差分（微分）向量 float v2 = (float)img.at<sift_wt>(r, c)*2; float dxx = (img.at<sift_wt>(r, c+1) + img.at<sift_wt>(r, c-1) - v2)*second_deriv_scale;//对x轴的二阶微分 float dyy = (img.at<sift_wt>(r+1, c) + img.at<sift_wt>(r-1, c) - v2)*second_deriv_scale;//对y轴的二阶微分 float dss = (next.at<sift_wt>(r, c) + prev.at<sift_wt>(r, c) - v2)*second_deriv_scale; //对z轴的二阶微分 float dxy = (img.at<sift_wt>(r+1, c+1) - img.at<sift_wt>(r+1, c-1) - img.at<sift_wt>(r-1, c+1) + img.at<sift_wt>(r-1, c-1))*cross_deriv_scale; //对x，y轴的分别微分 float dxs = (next.at<sift_wt>(r, c+1) - next.at<sift_wt>(r, c-1) - prev.at<sift_wt>(r, c+1) + prev.at<sift_wt>(r, c-1))*cross_deriv_scale; //对x，z轴的分别微分 float dys = (next.at<sift_wt>(r+1, c) - next.at<sift_wt>(r-1, c) - prev.at<sift_wt>(r+1, c) + prev.at<sift_wt>(r-1, c))*cross_deriv_scale; //对y，z轴的分别微分 Matx33f H(dxx, dxy, dxs, dxy, dyy, dys, dxs, dys, dss); //组成的海森矩阵 //求解Hx=dD 负梯度方向（二阶梯度下降法） Vec3f X = H.solve(dD, DECOMP_LU); //梯度下降方向 xi = -X[2]; xr = -X[1]; xc = -X[0]; //设置终止条件，证明该点已经为极值点 if( std::abs(xi) < 0.5f && std::abs(xr) < 0.5f && std::abs(xc) < 0.5f ) break; //如果该点为发散的，则返回错误 if( std::abs(xi) > (float)(INT_MAX/3) || std::abs(xr) > (float)(INT_MAX/3) || std::abs(xc) > (float)(INT_MAX/3) ) return false; //进行梯度下降 c += cvRound(xc); r += cvRound(xr); layer += cvRound(xi); //如果点坐标（x，y，z）越界 则同样返回错误 if( layer < 1 || layer > nOctaveLayers || c < SIFT_IMG_BORDER || c >= img.cols - SIFT_IMG_BORDER || r < SIFT_IMG_BORDER || r >= img.rows - SIFT_IMG_BORDER ) return false; } // ensure convergence of interpolation 验证迭代次数没有大于最大迭代次数 if( i >= SIFT_MAX_INTERP_STEPS ) return false; { int idx = octv*(nOctaveLayers+2) + layer; //取该特征点所在差分金字塔的位置索引 const Mat& img = dog_pyr[idx]; const Mat& prev = dog_pyr[idx-1]; const Mat& next = dog_pyr[idx+1]; Matx31f dD((img.at<sift_wt>(r, c+1) - img.at<sift_wt>(r, c-1))*deriv_scale, (img.at<sift_wt>(r+1, c) - img.at<sift_wt>(r-1, c))*deriv_scale, (next.at<sift_wt>(r, c) - prev.at<sift_wt>(r, c))*deriv_scale); //微分向量 float t = dD.dot(Matx31f(xc, xr, xi)); //内积 将微分向量与梯度下降的方向做内积 //？？？？？？？？？？？？？？？？？？？？？？？？ contr = img.at<sift_wt>(r, c)*img_scale + t * 0.5f; if( std::abs( contr ) * nOctaveLayers < contrastThreshold ) return false; // principal curvatures are computed using the trace and det of Hessian // 避免计算特征值的麻烦，海森矩阵的特征值与主曲率成正比 ，这里用Tr(H)^2/Det(H)>edgeThreshold来近似代替主曲率 // 设a,b分别为海森矩阵特征值，则令r=a/b Tr(H)=a+b Det(H)=a*b Tr(H)^2/Det(H)=(r+1)^2/r float v2 = img.at<sift_wt>(r, c)*2.f; float dxx = (img.at<sift_wt>(r, c+1) + img.at<sift_wt>(r, c-1) - v2)*second_deriv_scale; float dyy = (img.at<sift_wt>(r+1, c) + img.at<sift_wt>(r-1, c) - v2)*second_deriv_scale; float dxy = (img.at<sift_wt>(r+1, c+1) - img.at<sift_wt>(r+1, c-1) - img.at<sift_wt>(r-1, c+1) + img.at<sift_wt>(r-1, c-1)) * cross_deriv_scale; float tr = dxx + dyy; float det = dxx * dyy - dxy * dxy; if( det <= 0 || tr*tr*edgeThreshold >= (edgeThreshold + 1)*(edgeThreshold + 1)*det ) return false; } // 特征点的精确位置（对应原始图像的位置（x,y）） kpt.pt.x = (c + xc) * (1 << octv); kpt.pt.y = (r + xr) * (1 << octv); // 特征点所在的族 kpt.octave = octv + (layer << 8) + (cvRound((xi + 0.5)*255) << 16); // 该特征点所在的尺度大小为：该特征点所在尺度 2^(octv+layer/nOctaveLayers)*sigma * 2 因为平时所说的尺度为半径，这里是长度 kpt.size = sigma*powf(2.f, (layer + xi) / nOctaveLayers)*(1 << octv)*2; kpt.response = std::abs(contr); return true; } // // Detects features at extrema in DoG scale space. Bad features are discarded // based on contrast and ratio of principal curvatures. void SIFT::findScaleSpaceExtrema( const vector<Mat>& gauss_pyr, const vector<Mat>& dog_pyr, vector<KeyPoint>& keypoints ) const { //由于gauss_pyr一共存在nOctaves*(nOctaveLayers + 3)幅图像 所以族数nOctaves = gauss_pyr.size()/(nOctaveLayers + 3); int nOctaves = (int)gauss_pyr.size()/(nOctaveLayers + 3); int threshold = cvFloor(0.5 * contrastThreshold / nOctaveLayers * 255 * SIFT_FIXPT_SCALE); const int n = SIFT_ORI_HIST_BINS; //将方向分为36个bin float hist[n]; KeyPoint kpt; keypoints.clear(); for( int o = 0; o < nOctaves; o++ ) for( int i = 1; i <= nOctaveLayers; i++ ) //注意这里是从第1张图像到第nOctaveLayers图像 而第0张图像和第nOctaveLayers+1张图像将不作处理，也是为什么我们要取nOctaveLayers+3张高斯图像的原因 { int idx = o*(nOctaveLayers+2)+i; //取差分金字塔当前族当前层的图像及其上一张图像和下一张图像 const Mat& img = dog_pyr[idx]; const Mat& prev = dog_pyr[idx-1]; const Mat& next = dog_pyr[idx+1]; int step = (int)img.step1(); int rows = img.rows, cols = img.cols; for( int r = SIFT_IMG_BORDER; r < rows-SIFT_IMG_BORDER; r++) { const sift_wt* currptr = img.ptr<sift_wt>(r); const sift_wt* prevptr = prev.ptr<sift_wt>(r); const sift_wt* nextptr = next.ptr<sift_wt>(r); for( int c = SIFT_IMG_BORDER; c < cols-SIFT_IMG_BORDER; c++) { sift_wt val = currptr[c]; // find local extrema with pixel accuracy 如果该点大于三维坐标系下周边所有临近的26个点，才证明该点有可能是极值点 if( std::abs(val) > threshold && ((val > 0 && val >= currptr[c-1] && val >= currptr[c+1] && val >= currptr[c-step-1] && val >= currptr[c-step] && val >= currptr[c-step+1] && val >= currptr[c+step-1] && val >= currptr[c+step] && val >= currptr[c+step+1] && val >= nextptr[c] && val >= nextptr[c-1] && val >= nextptr[c+1] && val >= nextptr[c-step-1] && val >= nextptr[c-step] && val >= nextptr[c-step+1] && val >= nextptr[c+step-1] && val >= nextptr[c+step] && val >= nextptr[c+step+1] && val >= prevptr[c] && val >= prevptr[c-1] && val >= prevptr[c+1] && val >= prevptr[c-step-1] && val >= prevptr[c-step] && val >= prevptr[c-step+1] && val >= prevptr[c+step-1] && val >= prevptr[c+step] && val >= prevptr[c+step+1]) || (val < 0 && val <= currptr[c-1] && val <= currptr[c+1] && val <= currptr[c-step-1] && val <= currptr[c-step] && val <= currptr[c-step+1] && val <= currptr[c+step-1] && val <= currptr[c+step] && val <= currptr[c+step+1] && val <= nextptr[c] && val <= nextptr[c-1] && val <= nextptr[c+1] && val <= nextptr[c-step-1] && val <= nextptr[c-step] && val <= nextptr[c-step+1] && val <= nextptr[c+step-1] && val <= nextptr[c+step] && val <= nextptr[c+step+1] && val <= prevptr[c] && val <= prevptr[c-1] && val <= prevptr[c+1] && val <= prevptr[c-step-1] && val <= prevptr[c-step] && val <= prevptr[c-step+1] && val <= prevptr[c+step-1] && val <= prevptr[c+step] && val <= prevptr[c+step+1]))) { int r1 = r, c1 = c, layer = i; //将极值点进行差值精确找到极值点的位置，提高精度的位极值点的x,y坐标以及该极值点所处的层数layer 注意并不优化极值点所在的族数 //并且该函数将剔除差分金字塔的边缘效应 if( !adjustLocalExtrema(dog_pyr, kpt, o, layer, r1, c1, nOctaveLayers, (float)contrastThreshold, (float)edgeThreshold, (float)sigma) ) continue; //计算该特征点所在层数相对于该族第0层图像的尺度比例 sigma float scl_octv = kpt.size*0.5f/(1 << o); //计算该特征点在高斯金字塔下的方向梯度直方图 float omax = calcOrientationHist(gauss_pyr[o*(nOctaveLayers+3) + layer], Point(c1, r1), cvRound(SIFT_ORI_RADIUS * scl_octv), //// 9sigma/2 SIFT_ORI_SIG_FCTR * scl_octv, // 3sigma/2 hist, n); float mag_thr = (float)(omax * SIFT_ORI_PEAK_RATIO); //将所有hist值大于主方向对应hist值得所有方向都作为特征点的方向加入特征点vector容器中 找寻辅助方向 for( int j = 0; j < n; j++ ) { int l = j > 0 ? j - 1 : n - 1; int r2 = j < n-1 ? j + 1 : 0; if( hist[j] > hist[l] && hist[j] > hist[r2] && hist[j] >= mag_thr ) { float bin = j + 0.5f * (hist[l]-hist[r2]) / (hist[l] - 2*hist[j] + hist[r2]); bin = bin < 0 ? n + bin : bin >= n ? bin - n : bin; kpt.angle = 360.f - (float)((360.f/n) * bin); if(std::abs(kpt.angle - 360.f) < FLT_EPSILON) kpt.angle = 0.f; keypoints.push_back(kpt); } } } } } } } // Computes a gradient orientation histogram at a specified pixel //在高斯金字塔下计算特征点的梯度直方图 static float calcOrientationHist( const Mat& img, Point pt, int radius, float sigma, float* hist, int n ) { int i, j, k, len = (radius*2+1)*(radius*2+1); float expf_scale = -1.f/(2.f * sigma * sigma); AutoBuffer<float> buf(len*4 + n+4); //为下面的变量开辟地址空间 float *X = buf, *Y = X + len, *Mag = X, *Ori = Y + len, *W = Ori + len; float* temphist = W + len + 2; for( i = 0; i < n; i++ ) //36个bin temphist数组存储该bin的权值 temphist[i] = 0.f; for( i = -radius, k = 0; i <= radius; i++ ) { int y = pt.y + i; if( y <= 0 || y >= img.rows - 1 ) continue; for( j = -radius; j <= radius; j++ ) { int x = pt.x + j; if( x <= 0 || x >= img.cols - 1 ) continue; float dx = (float)(img.at<sift_wt>(y, x+1) - img.at<sift_wt>(y, x-1)); float dy = (float)(img.at<sift_wt>(y-1, x) - img.at<sift_wt>(y+1, x)); // X为每个特征点对应范围内x方向的梯度 Y对应的是每个特征点对应范围内y方向的梯度 W是每个特征点对应范围内的权值 X[k] = dx; Y[k] = dy; W[k] = (i*i + j*j)*expf_scale; k++; } } len = k; // compute gradient values, orientations and the weights over the pixel neighborhood // 梯度的权值 根据高斯核的尺度sigma决定（半径大小） exp(W, W, len); // 梯度的幅角 fastAtan2(Y, X, Ori, len, true); // 梯度的幅值 magnitude(X, Y, Mag, len); for( k = 0; k < len; k++ ) { int bin = cvRound((n/360.f)*Ori[k]); //计算当前角度属于哪个bin if( bin >= n ) bin -= n; if( bin < 0 ) bin += n; temphist[bin] += W[k]*Mag[k]; //根据幅值和权重加入到该bin的方向直方图中 } // smooth the histogram 对直方图进行滤波（高斯滤波） temphist[-1] = temphist[n-1]; temphist[-2] = temphist[n-2]; temphist[n] = temphist[0]; temphist[n+1] = temphist[1]; for( i = 0; i < n; i++ ) { hist[i] = (temphist[i-2] + temphist[i+2])*(1.f/16.f) + (temphist[i-1] + temphist[i+1])*(4.f/16.f) + temphist[i]*(6.f/16.f); } //得到主方向 对应最大的值 float maxval = hist[0]; for( i = 1; i < n; i++ ) maxval = std::max(maxval, hist[i]); return maxval; } //计算SIFT描述子 static void calcSIFTDescriptor( const Mat& img, Point2f ptf, float ori, float scl, int d, int n, float* dst ) { Point pt(cvRound(ptf.x), cvRound(ptf.y)); float cos_t = cosf(ori*(float)(CV_PI/180)); float sin_t = sinf(ori*(float)(CV_PI/180)); float bins_per_rad = n / 360.f; float exp_scale = -1.f/(d * d * 0.5f); float hist_width = SIFT_DESCR_SCL_FCTR * scl; //3*sigma 3sigma之外的点对当前点的影响不大，关联性不大（3sigma原则） int radius = cvRound(hist_width * 1.4142135623730951f * (d + 1) * 0.5f); //满足旋转型和三次线性插值 将半径变为此 // Clip the radius to the diagonal of the image to avoid autobuffer too large exception radius = std::min(radius, (int) sqrt((double) img.cols*img.cols + img.rows*img.rows)); cos_t /= hist_width; //为了计算时y''= 1/3sigma*(j * cos_t - i * sin_t) sin_t /= hist_width; //为了计算时x''= 1/3sigma*(j * sin_t + i * cos_t) int i, j, k, len = (radius*2+1)*(radius*2+1), histlen = (d+2)*(d+2)*(n+2); int rows = img.rows, cols = img.cols; AutoBuffer<float> buf(len*6 + histlen); float *X = buf, *Y = X + len, *Mag = Y, *Ori = Mag + len, *W = Ori + len; float *RBin = W + len, *CBin = RBin + len, *hist = CBin + len; for( i = 0; i < d+2; i++ ) { for( j = 0; j < d+2; j++ ) for( k = 0; k < n+2; k++ ) hist[(i*(d+2) + j)*(n+2) + k] = 0.; } for( i = -radius, k = 0; i <= radius; i++ ) for( j = -radius; j <= radius; j++ ) { // Calculate sample's histogram array coords rotated relative to ori. // Subtract 0.5 so samples that fall e.g. in the center of row 1 (i.e. // r_rot = 1.5) have full weight placed in row 1 after interpolation. //c_rot r_rot范围在-d/2~d/2 之间 cbin rbin范围在0~d之间 r,c是对应点的坐标 float c_rot = j * cos_t - i * sin_t; float r_rot = j * sin_t + i * cos_t; float rbin = r_rot + d/2 - 0.5f; float cbin = c_rot + d/2 - 0.5f; int r = pt.y + i, c = pt.x + j; if( rbin > -1 && rbin < d && cbin > -1 && cbin < d && r > 0 && r < rows - 1 && c > 0 && c < cols - 1 ) { float dx = (float)(img.at<sift_wt>(r, c+1) - img.at<sift_wt>(r, c-1)); float dy = (float)(img.at<sift_wt>(r-1, c) - img.at<sift_wt>(r+1, c)); //X[k] Y[k]存储的是对应点相对于x轴y轴的梯度 RBin[k] CBin[k]存储的是对应点转化成0-d的坐标 X[k] = dx; Y[k] = dy; RBin[k] = rbin; CBin[k] = cbin; //权重 W[k] = (c_rot * c_rot + r_rot * r_rot)*exp_scale; k++; } } // radius*radius的范围内点的个数 len = k; //计算梯度的方向，幅值，以及权重 fastAtan2(Y, X, Ori, len, true); magnitude(X, Y, Mag, len); exp(W, W, len); //遍历radius*radius的范围内所有的点 for( k = 0; k < len; k++ ) { float rbin = RBin[k], cbin = CBin[k]; float obin = (Ori[k] - ori)*bins_per_rad; //相对于主方向的角度 float mag = Mag[k]*W[k]; //当前点的梯度权值 int r0 = cvFloor( rbin ); int c0 = cvFloor( cbin ); int o0 = cvFloor( obin ); rbin -= r0; //dr 对于邻近两行的贡献因子dr和1-dr cbin -= c0; //dc 对于邻近两列的贡献因子dc和1-dc obin -= o0; //do 对于邻近两个方向的贡献因子为do和 1-do if( o0 < 0 ) o0 += n; if( o0 >= n ) o0 -= n; // histogram update using tri-linear interpolation 三次线性插值 计算每个点对于所处的bin以及相邻bin的权重 float v_r1 = mag*rbin, v_r0 = mag - v_r1; float v_rc11 = v_r1*cbin, v_rc10 = v_r1 - v_rc11; float v_rc01 = v_r0*cbin, v_rc00 = v_r0 - v_rc01; float v_rco111 = v_rc11*obin, v_rco110 = v_rc11 - v_rco111; float v_rco101 = v_rc10*obin, v_rco100 = v_rc10 - v_rco101; float v_rco011 = v_rc01*obin, v_rco010 = v_rc01 - v_rco011; float v_rco001 = v_rc00*obin, v_rco000 = v_rc00 - v_rco001; int idx = ((r0+1)*(d+2) + c0+1)*(n+2) + o0; hist[idx] += v_rco000; hist[idx+1] += v_rco001; hist[idx+(n+2)] += v_rco010; hist[idx+(n+3)] += v_rco011; hist[idx+(d+2)*(n+2)] += v_rco100; hist[idx+(d+2)*(n+2)+1] += v_rco101; hist[idx+(d+3)*(n+2)] += v_rco110; hist[idx+(d+3)*(n+2)+1] += v_rco111; } // finalize histogram, since the orientation histograms are circular 最终的梯度直方图 for( i = 0; i < d; i++ ) for( j = 0; j < d; j++ ) { int idx = ((i+1)*(d+2) + (j+1))*(n+2); hist[idx] += hist[idx+n]; hist[idx+1] += hist[idx+n+1]; for( k = 0; k < n; k++ ) dst[(i*d + j)*n + k] = hist[idx+k]; } // copy histogram to the descriptor, // apply hysteresis thresholding // and scale the result, so that it can be easily converted // to byte array float nrm2 = 0; // 4*4*8 描述子向量的个数 //描述子中128维向量存储的是4*4个小方格里8个方向分别的权重和 （先归一化然后在将0-1float数转化为 255的uchar数） len = d*d*n; for( k = 0; k < len; k++ ) nrm2 += dst[k]*dst[k]; float thr = std::sqrt(nrm2)*SIFT_DESCR_MAG_THR;//添加阈值，向量二范数大于向量归一化后0.2，则认为是由于非线性光照造成的 for( i = 0, nrm2 = 0; i < k; i++ ) //重新计算h^2的和 { float val = std::min(dst[i], thr); dst[i] = val; nrm2 += val*val; } nrm2 = SIFT_INT_DESCR_FCTR/std::max(std::sqrt(nrm2), FLT_EPSILON); #if 1 for( k = 0; k < len; k++ ) { dst[k] = saturate_cast<uchar>(dst[k]*nrm2); //对向量进行归一化并转化为uchar型 } #else float nrm1 = 0; for( k = 0; k < len; k++ ) { dst[k] *= nrm2; nrm1 += dst[k]; } nrm1 = 1.f/std::max(nrm1, FLT_EPSILON); for( k = 0; k < len; k++ ) { dst[k] = std::sqrt(dst[k] * nrm1);//saturate_cast<uchar>(std::sqrt(dst[k] * nrm1)*SIFT_INT_DESCR_FCTR); } #endif } static void calcDescriptors(const vector<Mat>& gpyr, const vector<KeyPoint>& keypoints, Mat& descriptors, int nOctaveLayers, int firstOctave ) { int d = SIFT_DESCR_WIDTH, n = SIFT_DESCR_HIST_BINS; //找寻检测到的没各特征点的 for( size_t i = 0; i < keypoints.size(); i++ ) { KeyPoint kpt = keypoints[i]; int octave, layer; float scale; unpackOctave(kpt, octave, layer, scale); CV_Assert(octave >= firstOctave && layer <= nOctaveLayers+2); float size=kpt.size*scale; Point2f ptf(kpt.pt.x*scale, kpt.pt.y*scale); //在高斯金字塔下计算描述子 const Mat& img = gpyr[(octave - firstOctave)*(nOctaveLayers + 3) + layer]; float angle = 360.f - kpt.angle; if(std::abs(angle - 360.f) < FLT_EPSILON) angle = 0.f; //img为高斯金字塔下的图像 ptf也是高斯金字塔下对应层数的坐标 calcSIFTDescriptor(img, ptf, angle, size*0.5f, d, n, descriptors.ptr<float>((int)i)); } } void SIFT::operator()(InputArray _image, InputArray _mask, vector<KeyPoint>& keypoints, OutputArray _descriptors, bool useProvidedKeypoints) const { int firstOctave = -1, actualNOctaves = 0, actualNLayers = 0; Mat image = _image.getMat(), mask = _mask.getMat(); if( image.empty() || image.depth() != CV_8U ) CV_Error( CV_StsBadArg, "image is empty or has incorrect depth (!=CV_8U)" ); if( !mask.empty() && mask.type() != CV_8UC1 ) CV_Error( CV_StsBadArg, "mask has incorrect type (!=CV_8UC1)" ); if( useProvidedKeypoints ) { firstOctave = 0; int maxOctave = INT_MIN; for( size_t i = 0; i < keypoints.size(); i++ ) { int octave, layer; float scale; unpackOctave(keypoints[i], octave, layer, scale); firstOctave = std::min(firstOctave, octave); maxOctave = std::max(maxOctave, octave); actualNLayers = std::max(actualNLayers, layer-2); } firstOctave = std::min(firstOctave, 0); CV_Assert( firstOctave >= -1 && actualNLayers <= nOctaveLayers ); actualNOctaves = maxOctave - firstOctave + 1; } Mat base = createInitialImage(image, firstOctave < 0, (float)sigma); vector<Mat> gpyr, dogpyr; int nOctaves = actualNOctaves > 0 ? actualNOctaves : cvRound(log( (double)std::min( base.cols, base.rows ) ) / log(2.) - 2) - firstOctave; //double t, tf = getTickFrequency(); //t = (double)getTickCount(); buildGaussianPyramid(base, gpyr, nOctaves); buildDoGPyramid(gpyr, dogpyr); //t = (double)getTickCount() - t; //printf("pyramid construction time: %g\n", t*1000./tf); if( !useProvidedKeypoints ) { //t = (double)getTickCount(); findScaleSpaceExtrema(gpyr, dogpyr, keypoints); //去除重复点 KeyPointsFilter::removeDuplicated( keypoints ); //从中选取最优的前nfeatures个特征点 if( nfeatures > 0 ) KeyPointsFilter::retainBest(keypoints, nfeatures); //t = (double)getTickCount() - t; //printf("keypoint detection time: %g\n", t*1000./tf); if( firstOctave < 0 ) for( size_t i = 0; i < keypoints.size(); i++ ) { KeyPoint& kpt = keypoints[i]; float scale = 1.f/(float)(1 << -firstOctave); kpt.octave = (kpt.octave & ~255) | ((kpt.octave + firstOctave) & 255); kpt.pt *= scale; kpt.size *= scale; } if( !mask.empty() ) KeyPointsFilter::runByPixelsMask( keypoints, mask ); } else { // filter keypoints by mask //KeyPointsFilter::runByPixelsMask( keypoints, mask ); } if( _descriptors.needed() ) { //t = (double)getTickCount(); int dsize = descriptorSize(); _descriptors.create((int)keypoints.size(), dsize, CV_32F); Mat descriptors = _descriptors.getMat(); calcDescriptors(gpyr, keypoints, descriptors, nOctaveLayers, firstOctave); //t = (double)getTickCount() - t; //printf("descriptor extraction time: %g\n", t*1000./tf); } }
参考：
1.基于SIFT特征目标跟踪算法研究 蔺海峰 马宇峰 宋涛
2.https://blog.csdn.net/u010440456/article/details/81483145
3.https://blog.csdn.net/qq_30356613/article/details/78534101
