牛客网 剑指offer-JZ10 矩形覆盖

描述

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，从同一个方向看总共有多少种不同的方法？

 

比如n=3时，2*3的矩形块有3种不同的覆盖方法(从同一个方向看)：

 

 

 

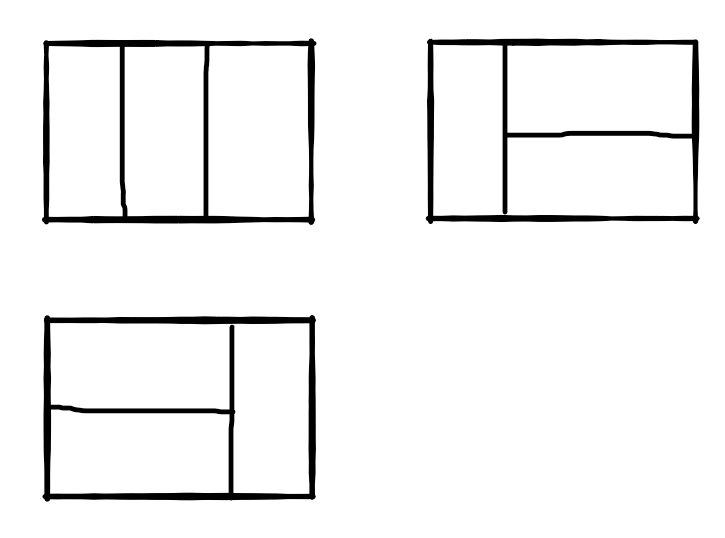
输入描述：

2*1的小矩形的总个数n

返回值描述：

覆盖一个2*n的大矩形总共有多少种不同的方法(从同一个方向看)

 

 

相应的结论应该是：

（1）1*3方块覆盖3*n区域：f(n) = f(n-1) + f(n - 3)， (n > 3)

（2）1*4方块覆盖4*n区域：f(n) = f(n-1) + f(n - 4)，(n > 4)

更一般的结论，如果用1*m的方块覆盖m*n区域，

递推关系式为f(n) = f(n-1) + f(n-m)，(n > m)。

 

 

class Solution:
    def rectCover(self, number):
        if number < 3:
            if(number == 0):    return 0
            if(number == 1):    return 1
            if(number == 2):    return 2
        else:
            g,f = 1,2
            while(number > 1) :
                f = f+g 
                g = f-g
                number -=1
            return g