矩阵在计算机程序中的应用
先总结一下矩阵运算的模版程序
求逆的方法目前不懂,求路过的大神解释。
/* 这部分请忽略
矩阵相乘有分治来优化的方法,Strassen算法,矩阵可以填0的方法计算令它成为2^n * 2^n,贴一下分治的那部分
void Strassen(int n, T A[][N], T B[][N], T C[][N]) { T A11[N][N], A12[N][N], A21[N][N], A22[N][N]; T B11[N][N], B12[N][N], B21[N][N], B22[N][N]; T C11[N][N], C12[N][N], C21[N][N], C22[N][N]; T M1[N][N], M2[N][N], M3[N][N], M4[N][N], M5[N][N], M6[N][N], M7[N][N]; T AA[N][N], BB[N][N]; if (n == 2) { //2-order Matrix_Multiply(A, B, C); } else { //将矩阵A和B分成阶数相同的四个子矩阵,即分治思想。 for (int i = 0; i < n / 2; i++) { for (int j = 0; j < n / 2; j++) { A11[i][j] = A[i][j]; A12[i][j] = A[i][j + n / 2]; A21[i][j] = A[i + n / 2][j]; A22[i][j] = A[i + n / 2][j + n / 2]; B11[i][j] = B[i][j]; B12[i][j] = B[i][j + n / 2]; B21[i][j] = B[i + n / 2][j]; B22[i][j] = B[i + n / 2][j + n / 2]; } } //Calculate M1 = (A0 + A3) × (B0 + B3) Matrix_Add(n / 2, A11, A22, AA); Matrix_Add(n / 2, B11, B22, BB); Strassen(n / 2, AA, BB, M1); //Calculate M2 = (A2 + A3) × B0 Matrix_Add(n / 2, A21, A22, AA); Strassen(n / 2, AA, B11, M2); //Calculate M3 = A0 × (B1 - B3) Matrix_Sub(n / 2, B12, B22, BB); Strassen(n / 2, A11, BB, M3); //Calculate M4 = A3 × (B2 - B0) Matrix_Sub(n / 2, B21, B11, BB); Strassen(n / 2, A22, BB, M4); //Calculate M5 = (A0 + A1) × B3 Matrix_Add(n / 2, A11, A12, AA); Strassen(n / 2, AA, B22, M5); //Calculate M6 = (A2 - A0) × (B0 + B1) Matrix_Sub(n / 2, A21, A11, AA); Matrix_Add(n / 2, B11, B12, BB); Strassen(n / 2, AA, BB, M6); //Calculate M7 = (A1 - A3) × (B2 + B3) Matrix_Sub(n / 2, A12, A22, AA); Matrix_Add(n / 2, B21, B22, BB); Strassen(n / 2, AA, BB, M7); //Calculate C0 = M1 + M4 - M5 + M7 Matrix_Add(n / 2, M1, M4, AA); Matrix_Sub(n / 2, M7, M5, BB); Matrix_Add(n / 2, AA, BB, C11); //Calculate C1 = M3 + M5 Matrix_Add(n / 2, M3, M5, C12); //Calculate C2 = M2 + M4 Matrix_Add(n / 2, M2, M4, C21); //Calculate C3 = M1 - M2 + M3 + M6 Matrix_Sub(n / 2, M1, M2, AA); Matrix_Add(n / 2, M3, M6, BB); Matrix_Add(n / 2, AA, BB, C22); //Set the result to C[][N] for (int i = 0; i < n / 2; i++) { for (int j = 0; j < n / 2; j++) { C[i][j] = C11[i][j]; C[i][j + n / 2] = C12[i][j]; C[i + n / 2][j] = C21[i][j]; C[i + n / 2][j + n / 2] = C22[i][j]; } } } }
算法核心就是把每次相乘的8次矩阵相乘变成了7次乘法,看别小看这减少的1次乘法,因为每递归1次,性能就提高了1/8,比如对于1024*1024的矩阵,第1次先分解成7次512*512的矩阵相乘,对于512*512的矩阵,又可以继续递归分解成256*256的矩阵相乘,…,一直递归下去,假设分解到64*64的矩阵大小后就不再递归,那么所花的时间将是分块矩阵乘法的(7/8) * (7/8) * (7/8) * (7/8) = 0.586倍,提高了快接近一倍
*/
回归正题,看O(n^3)的矩阵乘法,这个在程序里就很可以了。
#include <iostream> #include <cmath> using namespace std; #define MAXN 4 #define zero(x) (fabs(x)<1e-8) struct mat { int n, m; double data[MAXN][MAXN]; mat(){ memset(data, 0, sizeof(data)); } }; void debug(mat tmp) { for (int i = 0; i < tmp.n; i++) { for (int j = 0; j < tmp.m; j++) printf("%.3lf ", tmp.data[i][j]); puts(""); } puts(""); } mat mul(mat& a, mat& b) { //a乘b = c int i, j, k; mat c; c.n = a.n, c.m = b.m; for (i = 0; i < c.n; i++) for (j = 0; j < c.m; j++) { for (c.data[i][j] = k = 0; k < a.m; k++) c.data[i][j] += a.data[i][k] * b.data[k][j]; //c.data[i][j] = (c.data[i][j] + ((LL) a.data[i][k] * b.data[k][j]) % mod) % mod; if (zero(c.data[i][j])) c.data[i][j] = 0; } return c; } mat pow(mat a, int x) { mat b; b.m = b.n = max(a.m, a.n); for (int i = 0; i < b.n; i++) b.data[i][i] = 1; while (x) { if (x & 1) { b = mul(a, b); } a = mul(a, a); x >>= 1; } return b; } //二分计算A^l+...A^r mat cal(mat A, int l, int r) { if (l == r) return pow(A, l); int m = (l + r + 1) / 2; mat t = cal(A, l, m - 1); //算前一半的和 mat t2 = pow(A, m - l); //中介的矩阵 t = add(t, mul(t2, t)); if ((r - l + 1) & 1) t = add(t, pow(A, r)); //如果是奇数,则加上最后一个 return t; } mat inv(mat a) { // 高斯—约旦法求逆矩阵 int i, j, k, is[MAXN], js[MAXN]; double t; for (k = 0; k < a.n; k++) { // 从第k行k列开始右下角子阵中选取绝对值最大的元素 记住元素所在行列号 for (t = 0, i = k; i < a.n; i++) for (j = k; j < a.n; j++) if (fabs(a.data[i][j]) > t) t = fabs(a.data[is[k] = i][js[k] = j]); if (is[k] != k) // 在通过行交换和列交换将它交换到主元素位置上 for (j = 0; j < a.n; j++) swap(a.data[k][j], a.data[is[k]][j]); if (js[k] != k) for (i = 0; i < a.n; i++) swap(a.data[i][k], a.data[i][js[k]]); a.data[k][k] = 1 / a.data[k][k]; for (j = 0; j < a.n; j++) if (j != k) a.data[k][j] *= a.data[k][k]; for (i = 0; i < a.n; i++) if (i != k) for (j = 0; j < a.n; j++) if (j != k) a.data[i][j] -= a.data[i][k] * a.data[k][j]; for (i = 0; i < a.n; i++) if (i != k) a.data[i][k] *= -a.data[k][k]; } for (k = a.n - 1; k >= 0; k--) { for (j = 0; j < a.n; j++) if (js[k] != k) swap(a.data[k][j], a.data[js[k]][j]); for (i = 0; i < a.n; i++) if (is[k] != k) swap(a.data[i][k], a.data[i][is[k]]); } return a; } double det(mat& a) { //求行列式 int i, j, k, sign = 0; double b[MAXN][MAXN], ret = 1, t; if (a.n != a.m) return 0; for (i = 0; i < a.n; i++) for (j = 0; j < a.m; j++) b[i][j] = a.data[i][j]; for (i = 0; i < a.n; i++) { if (zero(b[i][i])) { for (j = i + 1; j < a.n; j++) if (!zero(b[j][i])) break; if (j == a.n) return 0; for (k = i; k < a.n; k++) t = b[i][k], b[i][k] = b[j][k], b[j][k] = t; sign++; } ret *= b[i][i]; for (k = i + 1; k < a.n; k++) b[i][k] /= b[i][i]; for (j = i + 1; j < a.n; j++) for (k = i + 1; k < a.n; k++) b[j][k] -= b[j][i] * b[i][k]; } if (sign & 1) ret = -ret; return ret; } int main() { freopen("data3.txt", "r", stdin); int n, m; while (~scanf("%d%d", &n, &m)) { mat ma; ma.n = n, ma.m = m; for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) scanf("%lf", &ma.data[i][j]); mat ni = inv(ma); // debug(ni); puts(""); mat mu = mul(ma, ni); // debug(mu); } return 0; }
1.数学应用和图论应用(传递闭包)
先来说一下传递闭包的问题,就是离散数学中二元关系传递转化为矩阵相乘
比如POJ 3660这题,通过矩阵乘得到所有的有关系的二元点对,这题要求多少个点排名能够确定,就是知道这个点和所有其他点的胜负关系,转化为点的入度与出度和是否为n-1的问题
这题要注意,矩阵乘循环的顺序
#include <iostream> #include <cstdio> using namespace std; #define MAXN 110 int n; bool g[MAXN][MAXN]; void mul() { int i, j, k; for (k = 1; k <= n; k++) for (i = 1; i <= n; i++) for (j = 1; j <= n; j++) g[i][j] = g[i][j] | (g[i][k] & g[k][j]); } int main() { // freopen("data4.txt", "r", stdin); int m, u, v; scanf("%d%d", &n, &m); memset(g, 0, sizeof(g)); while (m--) { scanf("%d%d", &u, &v); g[u][v] = 1; } mul(); int cnt = 0; for (int i = 1; i <= n; i++) { int cnt_t = 0; for (int j = 1; j <= n; j++) if (g[i][j] || g[j][i]) { cnt_t++; } if (cnt_t == n - 1) cnt++; } cout << cnt << endl; return 0; }
1 给定一个有向图,问从A点恰好走k步(允许重复经过边)到达B点的方案数mod p的值
2 给出一张无向连通图,求S到E经过k条边的最短路
2.通过构造解决数学问题
我们先来考虑Fibonacci数列的递推公式,f[i] = f[i-1] + f[i-2]
我们可以用一个转移矩阵来表示这种转移
有一个矩阵 1 1 乘上 f[i-1] 得到 f[i]
1 0 f[i-2] f[i-1]
这样f[i-1]通过一个转移矩阵递推出f[i]
同理如 f[i] = a1*f[i-1] + a2*f[i-2] + ~~ + ak*f[i-k]
就可以找到矩阵 a1 a2 a3 ~~ ak 通过第一行来递增,通过之后的行来保留原来的值
1 0 0 ~~ 0
0 1 0 ~~ 0
| | | ~~ |
0 0 ~~ 1 0
则 f[n] = 转移矩阵^n * f[0] 更高效的求出 f[n]
另一个应用 矩阵表示向量的缩放,翻转,旋转,平移。
缩放,翻转,旋转 可以给坐标矩阵 x 乘上一个2*2矩阵得到,如缩放乘 k 0 翻转乘 1 0 旋转乘 cosa -sina
y 0 k 0 -1 sina cosa
但是不能满足平移操作的要求
我们的解决办法是加一个维度,用 x 来表示坐标,平移操作乘上矩阵 1 0 x
y 0 1 y
1 0 0 1
保证统一性,其他操作都变为3*3的矩阵,3行3列为1,其他补0。
找到一个很好地图说明

另外也可以解决对序列的置换
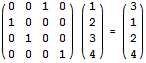
构造矩阵例题 HDU 1757
f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
|f(10) | |a0 a1 a2 ...a8 a9| |f(9)|
| f(9) | | 1 0 0 ... 0 0| |f(8)|
| .... | = |.. ... ... ... ..| | .. |
| f(2) | | 0 0 0 ... 0 0| |f(1)|
| f(1) | | 0 0 0 ... 1 0| |f(0)|
可见每次乘上这样一个构造矩阵就能降次
可以推出:
(f(n),f(n-1),...,f(n-9))^(-1) = A^(n-9)*(f(9),f(8),...,f(0))^(-1)
#include <cstdio> #include <vector> #include <algorithm> #include <queue> #include <cmath> using namespace std; #define MAXN 15 #define LL long long LL mod; struct mat { int n, m; int data[MAXN][MAXN]; }; void debug(mat tmp) { for (int i = 0; i < tmp.n; i++) { for (int j = 0; j < tmp.m; j++) printf("%d ", tmp.data[i][j]); puts(""); } puts(""); } mat mul(mat& a, mat& b) { //a乘b = c int i, j, k; mat c; c.n = a.n, c.m = b.m; for (i = 0; i < c.n; i++) for (j = 0; j < c.m; j++) { for (c.data[i][j] = k = 0; k < a.m; k++) c.data[i][j] += (a.data[i][k] * b.data[k][j]) % mod; c.data[i][j] = (c.data[i][j] + mod) % mod; } return c; } mat pow(mat a, int x) { mat b; memset(b.data, 0, sizeof(b.data)); b.m = b.n = max(a.m, a.n); for (int i = 0; i < b.n; i++) b.data[i][i] = 1; while (x) { if (x & 1) { b = mul(a, b); } a = mul(a, a); x >>= 1; } return b; } int main() { // freopen("data3.txt", "r", stdin); mat tran; tran.m = tran.n = 10; int k; LL ans; while (~scanf("%d%I64d", &k, &mod)) { memset(tran.data, 0, sizeof(tran.data)); for (int i = 0; i < 10; i++) { scanf("%d", &tran.data[0][i]); tran.data[i + 1][i] = 1; } if (k < 10) { printf("%I64d\n", k % mod); continue; } tran = pow(tran, k - 9); ans = 0; for (int i = 0; i < 10; i++) ans += (tran.data[0][i] * (9 - i)) % mod; ans = (ans + mod) % mod; printf("%I64d\n", ans % mod); } return 0; }
2.HDU 2294
好难。推好递推公式后,难点就是怎么优化递推过程,就是构造一个递推矩阵,也要注意要经常取模
f[i][j]代表j种颜色组成i个珠子,有方程f[i][j]=f[i-1][j]*j+f[i-1][j-1]*(k-j-1),但由于N较大采用一般的方法DP必然按会超时的。
优化的方法是使用矩阵来做。将F[i-1]到F[i]的转移用矩阵来描述,相当于一个k*k的线性变换矩阵。因此F[i]=A*F[i-1],这里A是转移矩阵,即F[i]=Ai-1*F[1],所以F[1]+…+F[n]=A0*F[1]+…+An-1*F[1]=(E+A+A2+…+An-1)*F[1]。
0 k 0 0 0 0
0 1 k-1 0 0 0
0 0 2 0 0 0
. . . . . .
. . . . . .
0 0 0 0 k-1 1
0 0 0 0 0 k
for(i=1;i<=k;i++) //转移矩阵A
a[i-1][i]=k-i+1, a[i][i]=i;
#include<cstdio> #include<string.h> #include <iostream> using namespace std; int cas, n, k; #define MAXN 40 #define LL long long const int mod = 1234567891; struct mat { int n, m; int data[MAXN][MAXN]; mat() { n = m = 0; memset(data, 0, sizeof(data)); } }; void debug(mat tmp) { for (int i = 0; i < tmp.n; i++) { for (int j = 0; j < tmp.m; j++) printf("%d ", tmp.data[i][j]); puts(""); } puts(""); } mat mul(mat& a, mat& b) { //a乘b = c int i, j, k; mat c; c.n = a.n, c.m = b.m; for (i = 0; i < c.n; i++) for (j = 0; j < c.m; j++) { for (c.data[i][j] = k = 0; k < a.m; k++) c.data[i][j] = (c.data[i][j] + ((LL) a.data[i][k] * b.data[k][j]) % mod) % mod; } return c; } mat pow(mat a, int x) { mat b; b.m = b.n = max(a.m, a.n); for (int i = 0; i < b.n; i++) b.data[i][i] = 1; while (x) { if (x & 1) { b = mul(a, b); } a = mul(a, a); x >>= 1; } return b; } mat add(mat a, mat b) { //矩阵乘法 mat c; c.m = a.m, c.n = a.n; for (int i = 0; i < a.n; i++) for (int j = 0; j < a.m; j++) c.data[i][j] = ((LL) a.data[i][j] + b.data[i][j]) % mod; return c; } //二分计算A^l+...A^r mat cal(mat A, int l, int r) { if (l == r) return pow(A, l); int m = (l + r + 1) / 2; mat t = cal(A, l, m - 1); //算前一半的和 mat t2 = pow(A, m - l); //中介的矩阵 t = add(t, mul(t2, t)); if ((r - l + 1) & 1) t = add(t, pow(A, r)); //如果是奇数,则加上最后一个 return t; } int main() { // freopen("data3.txt", "r", stdin); scanf("%d", &cas); while (cas--) { scanf("%d%d", &n, &k); mat A; A.m = A.n = k + 1; for (int i = 1; i <= k; i++) //转移矩阵A A.data[i - 1][i] = k - i + 1, A.data[i][i] = i; printf("%d\n", cal(A, k, n).data[0][k]); } return 0; }
3.高斯消元解线性方程
1.求有唯一解的线性方程组
#include<cstdio> #include<cmath> using namespace std; int n, m; double ans[55], d[55][55], eps = 1e-9; int gauss_cpivot(double a[55][55], int n, double x[]) { int i, j, k, p; for (j = 0; j < n; ++j) { for (i = j + 1, p = j; i < n; ++i) if (fabs(a[i][j]) > fabs(a[p][j])) p = i; if (fabs(a[p][j]) < eps) return 0; if (p != j) for (k = j; k <= n; ++k) swap(a[j][k], a[p][k]); for (i = j + 1; i < n; ++i) for (k = n; k >= j; --k) a[i][k] -= a[j][k] * a[i][j] / a[j][j]; } for (j = n - 1; j >= 0; --j) { x[j] = a[j][n] / a[j][j]; for (i = j - 1; i >= 0; --i) a[i][n] -= a[i][j] * x[j]; } return 1; }
2.求系数行列式的秩判断是否有解
POJ 1830 用高斯消元解决开关问题: 每个开关只用一次,最后到达使若干个开关状态改变
可以发现对于每个开关从起始状态到终止状态都是那些对它有影响的开关开启关闭情况的异或,即用每个开关一个相关开关方程(相关为1,不相关为0)
那每个开关 系数以相关开关为1 建立一个异或的线性方程组 高斯消元看是否有解,有解每个解都是一种满足条件的方法,则方法数就是自由未知量的所有状态数
#include<cstdio> #include<cmath> #include<algorithm> using namespace std; #define MAXN 109 const double eps = 1e-8; inline bool ZERO(double a) { return fabs(a) < eps; } double d[55][55]; int R(double a[55][55], int r, int c) { //求系数行列式的秩 int i, j, R, k, Max; for (R = j = 0; j < c - 1; j++) { for (i = R + 1, Max = R; i < r; i++) if (fabs(a[i][j]) > fabs(a[Max][j])) Max = i; if (Max != R) for (k = j; k < c; k++) swap(a[R][k], a[Max][k]); if (ZERO(a[R][j])) { continue; } for (i = R + 1; i < r; i++) if (!ZERO(a[i][j])) { double t = a[i][j] / a[R][j]; for (k = j; k < c; k++) a[i][k] -= a[R][k] * t; } R++; } for (i = R; i < r; i++) { //无解情况 if (!ZERO(a[i][c - 1])) return -1; } return R; } int start[MAXN]; int end[MAXN]; int main() { // freopen("data3.txt", "r", stdin); int u, v; int T; int n; scanf("%d", &T); while (T--) { scanf("%d", &n); for (int i = 0; i < n; i++) scanf("%d", &start[i]); for (int i = 0; i < n; i++) scanf("%d", &end[i]); memset(d, 0, sizeof(d)); while (scanf("%d%d", &u, &v) && u && v) { d[v - 1][u - 1] = 1; } for (int i = 0; i < n; i++) d[i][i] = 1; for (int i = 0; i < n; i++) d[i][n] = start[i] ^ end[i]; int ans = R(d, n, n + 1); if (ans == -1) printf("Oh,it's impossible~!!\n"); else printf("%d\n", 1 << (n - ans)); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号