结对编程
作者:蒋权 陈庆生
一,Github地址:https://github.com/Cercis-chinensis/PTESSM
二,PSP2.1表格
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
150 |
120 |
|
· Estimate |
· 估计这个任务需要多少时间 |
150 |
120 |
|
Development |
开发 |
1680 |
2280 |
|
· Analysis |
· 需求分析 (包括学习新技术) |
60 |
60 |
|
· Design Spec |
· 生成设计文档 |
150 |
250 |
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
30 |
130 |
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
20 |
30 |
|
· Design |
· 具体设计 |
120 |
150 |
|
· Coding |
· 具体编码 |
1200 |
1500 |
|
· Code Review |
· 代码复审 |
60 |
80 |
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
40 |
80 |
|
Reporting |
报告 |
90 |
120 |
|
· Test Report |
· 测试报告 |
50 |
80 |
|
· Size Measurement |
· 计算工作量 |
20 |
20 |
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
20 |
20 |
|
合计 |
1830 |
2400 |
三,效能分析
1,使用逆波兰表达式。在设计生成题目算法时,我们一开始讨论打算将插入的操作数、运算符号的位置与内容,分别用数组存放,但是后来发现在将括号进行随机插入,会造成各种繁琐的情况。同时在设计计算题目算法时,我们根据各种算术表达式的情况,思考着设计出一个统一的计算算法,考虑过直接读取数字和字符来计算,还考虑过递归,但实现起来很繁琐或是有漏洞。后来我们查阅资料,找到一种可以方便且高效的计算方法,即利用逆波兰表达式,利用中缀转后缀得到逆波兰表达式,然后由此来给电脑进行计算,使得计算的效率显著提高 。
2,统一数值形式。将所有数值化为分数形式,即如:8 -> 8/1 等。一开始是,数值部分有整数还有分数两种形式。两种形式的相互计算的情况有很多种,颇为繁琐。于是统一形式,在最后再转化。
四,设计实现流程
心路历程:
一,生成题目
生成题目时使用rand()函数随机生成操作数的值与操作数的个数,以及生成比操作数个数少一位的运算符号,将操作数和运算符号进行组合然后在合适的位置随机插入或不插入括号(操作数之前或之后)。
二.计算题目
当生成了一道题目之后将题目存入ArrayList中,在计算之前首先将题目从中缀表达式转为后缀表达式,之后用栈来进行计算。将结果存入文本中。
三.检验答案
分别用两个BufferedReader读取用于检测的文本与正确的答案文本,在用两个String一行一行的读取文本内容然后进行比较,如果相等则正确数加一,记录此时的行数,否则错误数加一,记录此时的行数。最后输出结果。
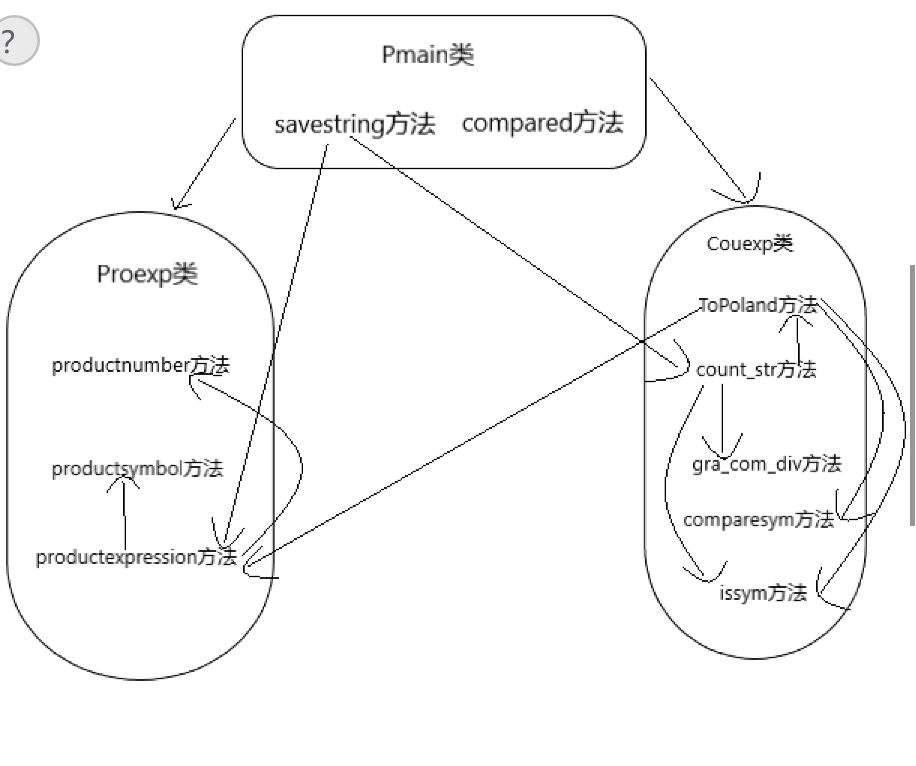
在分析好需求后,再根据所要实现功能,计划编写三个类,分别是class Proexp(用于生成题目算术表达式),Coexp类(用于计算上面产生的算术表达式),以及主类Pmain(用于处理从控制台传入的信息)。
类与方法:
一、Proexp类中:所编写的主要方法有:
1.ArrayList<String> productexpession(int n)
用于生成算术表达式。生成的表达式存进ArrayList数组里,因随机生成运算数的数量,无法预先声明数组的大小,故用此来避免这问题。在这个方法里面,利用下面两个方法所产生的数和符,按一定的次序组合成算术表达式,其中,括号,在合适的位置以一定的概率随机插入。具体看下面相应的代码说明。
2.ArrayList<String> productnumber(int n)
用于生成上面生成算术表达式所要用到的运算数。 返回的数组里的元素个数为2~4。为了后面运算方便,里面所生成的全是分数形式,其中生成分母为1的概率提高,使生成整数较多,同时转化为字符串传入数组。具体看下面的相关的代码说明。
3,ArrayList<String> productsymbol(int n)
用于生成上面生成算术表达式所要用到的运算符。 数目为运算数数量-1。随机生成4个操作符中的2个或3个。
二、Coexp类
1.ArrayList<String> ToPoland(ArrayList<String> e)
将生成的算术表达式转化为逆波兰表达式(中缀转后缀)。是为了便于后面对表达式的计算。这里利用栈于数组,实现表达式的转变。具体看下面的代码部分。
转化过程可参考:https://www.jianshu.com/p/fcd2b521a3e2
2 String count_str(ArrayList<String> e)
对逆波兰表达式进行运算。返回值为分数形式的字符串,后面还对该值进行化简。在计算过程中,利用栈进行运行。
3.int gra_com_div(int a, int b)
求最大公约数,用于化简分数。
4.boolean comparesym(String string, String peek)
用于判定优先级。
5.boolean issym(String string)
用于判定是否为操作符。
三、主类Pmain
1.void savestring(int i, ArrayList<String> str,FileWriter fw)
用于保存数组到文件中
2.void Compared
用于检查答案
流程图:
五,代码说明
1. productexpession(int n) 生成表达式
利用productnumber与productsymbol方法所随机产生的数和操作符,交替插入e数组中,同时,以一定的概率插入”(“,后面也以一定的概率在式中补全”)“,或在式子最后补全欠缺的右括号。
public ArrayList<String> productexpression(int n){ //n为数值范围
//num存储生成的数,sym存储运算符
ArrayList<String> num=productnumber(n);
ArrayList<String> sym=productsymbol(num.size()-1);
//e为算术表达式
ArrayList<String> e=new ArrayList<String>(20);
int d=0;//d记录左括数量,分析可以知道d<2.
for(int i=0, j=0 ;i<num.size();)
{
//随机以0.3的概率插入左括号
if(Math.random()<0.3&&d<2) { e.add("("); d++; }
else {
e.add(num.get(i));i++;
//随机以0.4的概率插入补全右括号
if(Math.random()<0.4 && e.size()>=2&&e.get(e.size()-2)!="("&& d>0 )
{e.add(")");d--;}
e.add(sym.get(j)); j++;
if(j==sym.size()) //遇到最后一个符号,自动补上剩下的最后一个数
{ e.add(num.get(i)); i++; }
}
}
while(d-- > 0) e.add(")");//补全 该补上的右括号。
return e;
}
2.productnumber(int n1)
生成数。数是以分数的形式表示,因为要求可以生成分数,可以统一数的形式,为了统一后面的计算过程,避免需要分开多种情况。同时设分母为1的概率为0.7,即增加为整数的概率。同时下面避免了分母为0。
private ArrayList<String> productnumber(int n1) {
// TODO Auto-generated method stub
ArrayList<String> num =new ArrayList<String>();//num用于储存所产生分数形式的运算数
Random r=new Random();
int m=r.nextInt(3)+2;//m为2到4,表示运算数的个数,最多4个。
for(int i=0;i<m;i++)
num.add(Integer.toString(r.nextInt(n1))+"/"+(Math.random()>0.3 ? "1":Integer.toString(r.nextInt(n1-1)+1)));
//(Math.random()>0.3 ? "1":Integer.toString(r.nextInt(n1-1)+1)) 这里用于控制以0.7的概率产生分母为1,同时控制分母不为0
return num;
}
3,生成运算符:
/////////////运算符
private ArrayList<String> productsymbol(int n2) {
// TODO Auto-generated method stub
ArrayList<String> sym =new ArrayList<String>();
String[] symbol=new String[] {"+","-","×","÷"};
for(int i=0;i<n2;i++) //控制生成n2-1个运算符。。
sym.add(symbol[(int) (Math.random()*symbol.length)]);//随机从数组中选
return sym;
}
}
4.转化为逆波兰表达式,即中缀转后缀
从左到右扫描中缀表达式,若是操作数,直接存入que;
若是运算符:
(1)该运算符是左括号 ( , 则直接存入 stack 栈。
(2)该运算符是右括号 ),则将 stack 栈中 ( 前的所有运算符出栈,存入 post 栈。
(3)若该运算符为非括号,则将该运算符和 stack 栈顶运算符作比较:若高于栈顶运算符,则直接存入 stack 栈,否则将栈顶运算符出栈(从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为止),存入 que。
(4)当扫描完后,stack 栈中还有运算符时,则将所有运算符出栈,存入 que。
public ArrayList<String> ToPoland(ArrayList<String> e){
//用于存储数还有后面的 逆波兰表达式
ArrayList<String> que=new ArrayList<String>();
Stack<String> stack=new Stack<String>();//存储符号,根据优先级进行入栈和出栈
for(int i=0;i<e.size();) {
if(!issym(e.get(i))) {//判断非运算符
que.add(e.get(i));i++;
}
else {
if(stack.isEmpty()) { stack.push(e.get(i)); i++; }
else if(e.get(i).equals(")")){//遇到右括号,符号出栈到que中,直到遇到左括号。
i++;
for(String s=stack.pop();!s.equals("(") ; ) {
que.add(s);
s=stack.pop();
}
}
else {
if(comparesym(e.get(i),stack.peek())) {
stack.push(e.get(i));
i++;
}
else {
do {//运算符出栈
que.add(stack.pop());
//判断栈非空以及运算符出栈直至遇到符号优先级比它高,
}while(!stack.isEmpty()&&!comparesym(e.get(i),stack.peek()));
}
}
}
}
while(!stack.empty()) que.add(stack.pop());
return que;
}
5.计算逆波兰表达式
从左到右扫描表达式,遇到数字就将其压入栈,遇到操作符表示可以计算,这时取出栈顶的两个元素进行操作,然后再次将结果压入栈,最后栈里会留下一个元素,该元素就是运行结果。
同时运算数化为分数形式,四则运算统一为分数之间的运算。
///计算波兰,
public String count_str(ArrayList<String> e) {
Stack<String> stack=new Stack<String>();//存储运算数以及最后计算结果
for(int i=0;i<e.size();) {
if(!issym(e.get(i))) {
stack.push(e.get(i));i++;// 数入栈
}else {
String str=e.get(i);i++;
String[] one=stack.pop().split("/");//第二个运算数
String[] two=stack.pop().split("/");//第一个运算数
int a=Integer.parseInt(two[0]); int b=Integer.parseInt(two[1]);//第一个运算数的分子与分母
int c=Integer.parseInt(one[0]); int d=Integer.parseInt(one[1]);//第二个运算数的分子与分母
int fson=0,fmom=0,divisor=1;
switch(str) {
case "+": fson=a*d+c*b; fmom=b*d;break;
case "-": fson=a*d-c*b; if(fson<0) return null ; fmom=b*d; break;
case "×": fson=a*c; fmom=b*d; break;
case "÷":fson=a*d;fmom=b*c; if (fmom==0)return null; break;
}
if(fson!=0&&fmom!=0)//防止 分子分母为0时,造成无法求最大公约数
divisor=gra_com_div(fson,fmom);//最大公约数
//将化简的分子分母,在以字符串形式入栈
stack.push(Integer.toString(fson/divisor)+"/"+Integer.toString(fmom/divisor));
}
}
return stack.pop();
}
6,辗转相除法求最大公约数
///求最大公约数,用于化简
private int gra_com_div(int a, int b) {
// TODO Auto-generated method stub
if(a<b) { a=a+b; b=a-b;a=a-b;} //a<b时,a, b互换
a=a%b;
if(a==0) return b;
else return gra_com_div(b,a);
}
7.写入文件,同时将假分数化为真分数
//x写入文件
static void savestring(int i, ArrayList<String> str,FileWriter fw) throws IOException {
//TO DO
fw.write((i+1)+"、");//开头形式,i为第i行
int j=0;
for(;j<str.size();) {
if(issym(str.get(j))) {
fw.write(" ");
fw.write(str.get(j));
j++;
fw.write(" ");
}
else {
String[] string=str.get(j).split("/"); j++;
int a=Integer.parseInt(string[0]);
int b=Integer.parseInt(string[1]);
int c=a/b; int d=a%b;
if(d==0)fw.write(Integer.toString(c));//遇到整数
else if(c!=0) fw.write(Integer.toString(c)+"'"+Integer.toString(d)+"/"+Integer.toString(b));//化为真分数形式
else fw.write(Integer.toString(d)+"/"+Integer.toString(b));
}
}
//此处j>1用于检测所传入字符是题目还是答案,是题目的话,后面加=号
if(j>1)fw.write(" =");
fw.write("\n");
}
六,测试运行
多次运行检测,在多次对比结果,以及对在答案方面是准确的
截图:
生成题目:

Exercise文件:(填写前)

Ansewr文件:

Exercises填答案后:

控制台输入检查答案的命令后:

此时查看Grade文件

认真对比后,答案正确
1,生成一万道题
题目
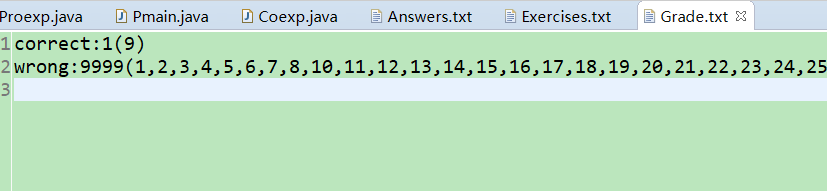
只答了第9题,检查结果为:
退出命令:

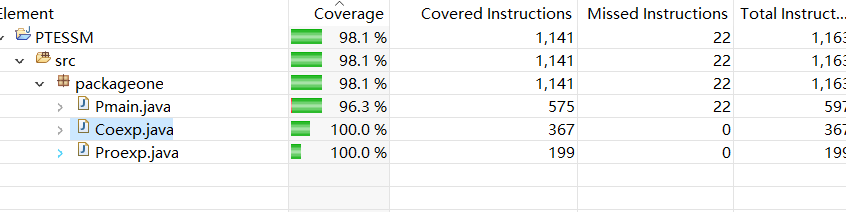
多输入测试后,除了一些抛出异常等语句外,其他代码基本都覆盖了。
代码覆盖率:
七,实际用时
更新至二表
八,总结
这次作业我们是第一次结对编程,各流程都很不熟悉,我们用了比较多时间在讨论上,特别再设计文档这一步,我们对算法进行了多次的修改与更换,寻求着一个没有漏洞的解决算法,想了多种方案,进度比较缓慢,因为我们都认为一个优秀的算法能够大大提高效率。通过本次作业我们巩固了 在开始编程之前要懂得分析需求,根据需求思考着要实现什么功能,对不同的功能思考着相应的实现方案,还要懂得查找更加优秀的算法并学习其思想,以此来改进我们的算法缩短工程量。
同时在一开始结对编程时,我们都感觉效率要比单独编程时低(因意见分歧而不断讨论),而在后面讨论出统一的方案后,后面的编程过程中能够感觉编程效率要高不少,或许以后配合默契之后效率会更高。同时,在讨论交流中,不同的思想在碰撞,很容易产生思维的火花,从而诞生很多新的想法。同时,在遇到不呢个解决的问题时,两人分别去查阅资料,效率很高。此外在编程中我们也更加深刻的认识到数学是设计更加高效算法的基础,优秀的算法能够更快更准确的解决问题。再次对前人的智慧感到敬佩。




